微积分的介绍-CSDN博客

本文链接：https://blog.csdn.net/back_room/article/details/131349663

微积分（Calculus），数学概念，是高等数学中研究函数的微分（Differentiation）、积分（Integration）以及有关概念和应用的数学分支。它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。

微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

中文名微积分

外文名 Calculus

所属学科数学、物理

研究内容切线、函数、极限、积分、微分

中心思想切线、函数

学科特点理论严密、应用广泛

微分发明艾萨克·牛顿、莱布尼茨

积分发明艾萨克·牛顿、莱布尼茨

微、积分关系互为逆运算

极限理论

编辑播报

十七世纪以来，微积分的概念和技巧不断扩展并被广泛应用来解决天文学、物理学中的各种实际问题，取得了巨大的成就。但直到十九世纪以前，在微积分的发展过程中，其数学分析的严密性问题一直没有得到解决。十八世纪中，包括牛顿和莱布尼兹在内的许多大数学家都觉察到这一问题并对这个问题作了努力，但都没有成功地解决这个问题。

整个十八世纪，微积分的基础是混乱和不清楚的，许多英国数学家也许是由于仍然为古希腊的几何所束缚，因而怀疑微积分的全部工作。这个问题一直到十九世纪下半叶才由法国数学家柯西得到了完整的解决，柯西极限存在准则使得微积分注入了严密性，这就是极限理论的创立。极限理论的创立使得微积分从此建立在一个严密的分析基础之上，它也为20世纪数学的发展奠定了基础。

注：在中世纪（14—17世纪）欧洲数学大发展的时期，我国基本处于停滞状态（明、清时期）。所以，中国的数学家与微积分无缘

微积分历史

从微积分成为一门学科来说，是在17世纪，但是积分的思想早在古代就已经产生了。

积分学早期史

公元前7世纪，古希腊科学家、哲学家泰勒斯就对球的面积、体积、与长度等问题的研究就含有微积分思想。公元前3世纪，古希腊的数学家、力学家阿基米德（公元前287年~公元前212年）的著作《圆的测量》和《论球与圆柱》中就已含有积分学的萌芽，他在研究解决抛物线下的弓形面积、球和球冠面积、螺线下的面积和旋转双曲线所得的体积的问题中就隐含着近代积分的思想。

中国古代数学家也产生过积分学的萌芽思想，例如三国时期的刘徽，他对积分学的思想主要有两点：割圆术及求体积问题的设想。微积分微积分产生到了十七世纪，有许多科学问题需要解决，这些问题也就成了促使微积分产生的因素。归结起来，大约有四种主要类型的问题：第一类是研究运动的时候直接出现的，也就是求即时速度的问题。第二类问题是求曲线的切线的问题。第三类问题是求函数的最大值和最小值问题。第四类问题是求曲线长、曲线围成的面积、曲面围成的体积、物体的重心、一个体积相当大的物体作用于另一物体上的引力。

数学首先从对运动（如天文、航海问题等）的研究中引出了一个基本概念，在那以后的二百年里，这个概念在几乎所有的工作中占中心位置，这就是函数——或变量间关系——的概念。紧接着函数概念的采用，产生了微积分，它是继欧几里得几何之后，全部数学中的一个最大的创造。围绕着解决上述四个核心的科学问题，微积分问题至少被十七世纪十几个最大的数学家和几十个小一些的数学家探索过。其创立者一般认为是牛顿和莱布尼茨。在此，我们主要来介绍这两位大师的工作。

实际上，在牛顿和莱布尼茨作出他们的冲刺之前，微积分的大量知识已经积累起来了。十七世纪的许多著名的数学家、天文学家、物理学家都为解决上述几类问题作了大量的研究工作，如法国的费马、笛卡尔、罗伯瓦、笛沙格；英国的巴罗、瓦里士；德国的开普勒；意大利的卡瓦列利等人都提出许多很有建树的理论。为微积分的创立做出了贡献。

例如费马、巴罗、笛卡尔都对求曲线的切线以及曲线围成的面积问题有过深入的研究，并且得到了一些结果，但是他们都没有意识到它的重要性。在十七世纪的前三分之二，微积分的工作沉没在细节里，作用不大的细微末节的推理使他们筋疲力尽了。只有少数几个大数学家意识到了这个问题，如詹姆斯·格里高利说过：“数学的真正划分不是分成几何和算术，而是分成普遍的和特殊的”。而这普遍的东西是由两个包罗万象的思想家牛顿和莱布尼茨提供的。

十七世纪下半叶，在前人工作的基础上，英国大科学家牛顿和德国数学家莱布尼茨分别在自己的国度里独自研究和完成了微积分的创立工作，虽然这只是十分初步的工作。他们的最大功绩是把两个貌似毫不相关的问题联系在一起，一个是切线问题（微分学的中心问题），一个是求积问题（积分学的中心问题）。

牛顿和莱布尼茨建立微积分的出发点是直观的无穷小量，因此这门学科早期也称为无穷小分析，这正是现时数学中分析学这一大分支名称的来源。牛顿研究微积分着重于从运动学来考虑，莱布尼茨却是侧重于几何学来考虑的。

牛顿的发展

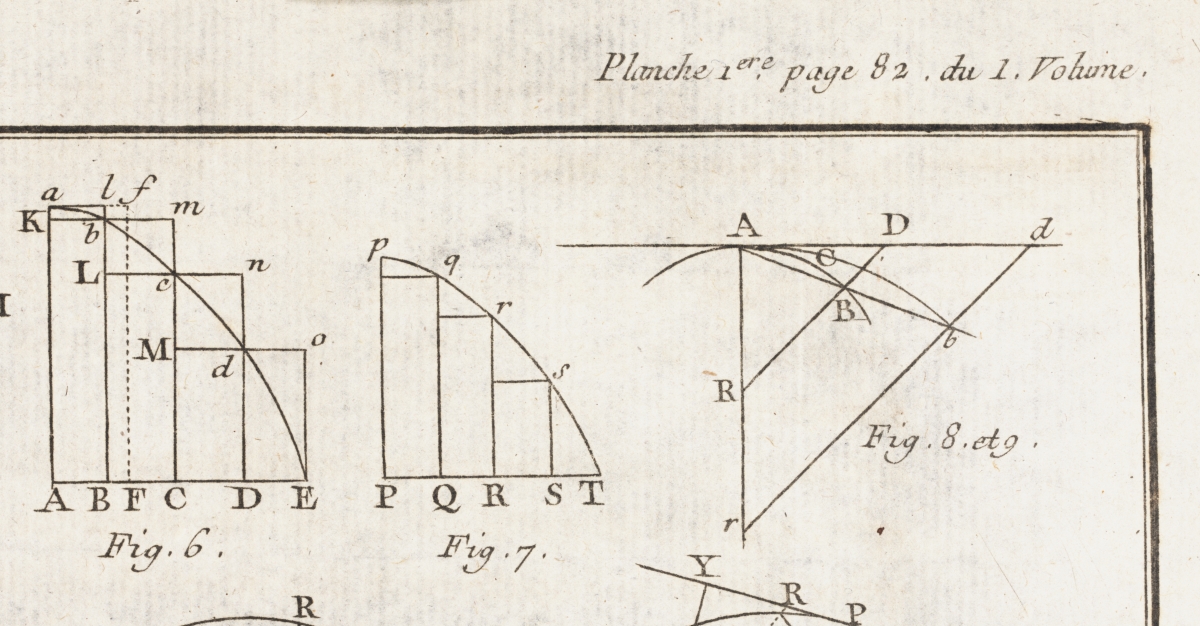
牛顿在1671年写了《流数术和无穷级数》，这本书直到1736年才出版，它在这本书里指出，变量是由点、线、面的连续运动产生的，否定了以前自己认为的变量是无穷小元素的静止集合。他把连续变量叫做流动量，把这些流动量的导数叫做流数。

牛顿在流数术中所提出的中心问题是：已知连续运动的路径，求给定时刻的速度（微分法）；已知运动的速度求给定时间内经过的路程（积分法）。 [5-6]

莱布尼茨

德国的莱布尼茨（又译“莱布尼兹”）是一个博才多学的学者，1684年，他发表了现在世界上认为是最早的微积分文献，这篇文章有一个很长而且很古怪的名字《一种求极大极小和切线的新方法，它也适用于分式和无理量，以及这种新方法的奇妙类型的计算》。就是这样一篇说理也颇含糊的文章，却有划时代的意义。它已含有现代的微分符号和基本微分法则。

1686年，莱布尼茨发表了第一篇积分学的文献。他是历史上最伟大的符号学者之一，他所创设的微积分符号，远远优于牛顿的符号，这对微积分的发展有极大的影响。现今我们使用的微积分通用符号就是当时莱布尼茨精心选用的。

优先权之争

编辑播报

微积分是能应用于许多类函数的一种新的普遍的方法，这一发现必须归功于牛顿和莱布尼茨两人。经过他们的工作，微积分不再是古希腊几何的附庸和延展，而是一门独立的学科。

历史上，关于微积分的成果归属和优先权问题，曾在数学界引起了一场长时间的大争论。1687年以前，牛顿没有发表过微积分方面的任何工作，虽然他从1665年到1687年把结果通知了他的朋友。特别地，1669年他把他的短文《分析学》术给了他的老师巴罗，后者把它送给了John Collins。莱布尼茨于1672年访问巴黎，1673年访问伦敦，并和一些与牛顿工作的人通信。然而，他直到1684年才发表微积分的著作。于是就发生莱布尼茨是否知道牛顿工作详情的问题，他被指责为剽窃者。但是，在这两个人死了很久以后，调查证明：虽然牛顿工作的大部分是在莱布尼兹之前做的，但是，莱布尼兹是微积分主要思想的独立发明人。

这场争吵的重要性不在于谁胜谁负的问题，而是使数学家分成两派。一派是英国数学家，捍卫牛顿；另一派是欧洲大陆数学家，尤其是伯努利兄弟，支持莱布尼茨，两派相互对立甚至敌对。其结果是，使得英国和欧洲大陆的数学家停止了思想交换。因为牛顿在关于微积分的主要工作和第一部出版物，即《自然哲学的数学原理》中使用了几何方法。所以在牛顿死后的一百多年里，英国人继续以几何为主要工具。而大陆的数学家继续莱布尼兹的分析法，使它发展并得到改善，这些事情的影响非常巨大，它不仅使英国的数学家落后在后面，而且使数学损失了一些最有才能的人应用可作出的贡献。

第二次危机

编辑播报

微积分诞生之后，数学迎来了一次空前繁荣的时期，对18世纪的数学产生了重要而深远的影响，但是牛顿和莱布尼茨的微积分都缺乏清晰的、严谨的逻辑基础，这在初创时期是不可避免的。科学上的巨大需要战胜了逻辑上的顾忌。他们需要做的事情太多了，他们急于去攫取新的成果。基本问题只好先放一放，正如达朗贝尔所说的：“向前进，你就会产生信心！”数学史的发展一再证明自由创造总是领先于形式化和逻辑基础。于是在微积分的发展过程中，出现了这样的局面：一方面是微积分创立之后立即在科学技术上获得应用，从而迅速地发展；另一方面是微积分学的理论在当时是不严密的，出现了越来越多的悖论和谬论。

数学的发展又遇到了深刻的令人不安的危机。例如，有时把无穷小量看作不为零的有限量而从等式两端消去，而有时却又令无穷小量为零而忽略不计。由于这些矛盾，引起了数学界的极大争论。如当时爱尔兰主教、唯心主义哲学家贝克莱嘲笑“无穷小量”是“已死的幽灵”。贝克莱对牛顿导数的定义进行了批判。

18世纪的分析学

驱动18世纪的微积分学不断向前发展的动力是物理学的需要，物理问题的表达一般都是用微分方程的形式。18世纪被称为数学史上的英雄世纪。他们把微积分应用于天文学、力学、光学、热学等各个领域，并获得了丰硕的成果。在数学本身又发展出了多元微分学、多重积分学、微分方程、无穷级数的理论、变分法，大大地扩展了数学研究的范围。其中最著名的要数最速降线问题：即最快下降的曲线的问题。这个曾经的难题用变分法的理论可以轻而易举的解决。 [7]

创立意义

编辑播报

微积分学的创立，极大地推动了数学的发展，过去很多用初等数学无法解决的问题，运用微积分，这些问题往往迎刃而解，显示出微积分学的非凡威力。

前面已经提到，一门学科的创立并不是某一个人的业绩，而是经过多少人的努力后，在积累了大量成果的基础上，最后由某个人或几个人总结完成的，微积分也是这样。

不幸的是，由于人们在欣赏微积分的宏伟功效之余，在提出谁是这门学科的创立者的时候，竟然引起了一场轩然大波，造成了欧洲大陆的数学家和英国数学家的长期对立。英国数学在一个时期里闭关锁国，囿于民族偏见，过于拘泥在牛顿的“流数术”中停步不前，因而数学发展落后了整整一百年。其实，牛顿和莱布尼茨分别是自己独立研究，在大体上相近的时间里先后完成的。比较特殊的是牛顿创立微积分要比莱布尼茨早10年左右，但是正式公开发表微积分这一理论，莱布尼茨却要比牛顿发表早三年。他们的研究各有长处，也都各有短处。那时候，由于民族偏见，关于发明优先权的争论竟从1699年始延续了一百多年。

应该指出，这是和历史上任何一项重大理论的完成都要经历一段时间一样，牛顿和莱布尼茨的工作也都是很不完善的。他们在无穷和无穷小量这个问题上，其说不一，十分含糊。牛顿的无穷小量，有时候是零，有时候不是零而是有限的小量；莱布尼茨的也不能自圆其说。这些基础方面的缺陷，最终导致了第二次数学危机的产生。

直到19世纪初，法国科学学院的科学家以柯西为首，对微积分的理论进行了认真研究，建立了极限理论，后来又经过德国数学家维尔斯特拉斯进一步的严格化，使极限理论成为了微积分的坚定基础。才使微积分进一步的发展开来。