监督学习应用之梯度下降

本博客说明

        本博客来源于斯坦福大学机器学习课程，对上课学到的知识进行梳理和整理，加上自己的一些思考，形成自己的笔记，有需要的可以借鉴。

线性回归算法

        线性回归简单来说就是用一条直线（一个变量时）来描述输入变量与输出之间的关系，并且可以通过这个关系对新输入的数据来预测。但是线性回归得出的模型并不一定是直线，当模型中有多个变量时，可能为一个平面或者更高维图形。
        线性回归的模型为：$$h(x)=x_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$$        假设${\theta }_0=1$,则线性回归模型可以表示为：$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i$$        也可以表示成矩阵形式：$$h(x)={\theta }^{T}x$$        为了使模型更准确真实的输出值，则可以采用最小二乘法。最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
        假设共有$m$组数据，$y$为实际值，则误差函数如下：$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(h_{\theta }(x_i)-y_i)$$        所以只需要找到$\theta$使得$J(\theta )$最小，就可以得到最接近真实数据的模型。

梯度下降法

        梯度下降法，是每走一步查看当前下降最快的方向，一定会停下来，但是可能会陷入局部最优解。梯度下降法依赖于参数初始值，由于初始值的不同，可能会陷入不同的局部最优解。其描述图如下：

        其中黑色线条描述了梯度下降的路径。梯度下降算法描述如下：

• 更新第$i$个参数的值：${\theta }_i:={\theta }_i-\alpha \frac{\partial }{\partial {\theta }_i}J(\theta )$，其中$\alpha$是一个参数，称为学习速度，它控制梯度下降的步长。如果步长太小，会使下降的速度过慢，从而花很长的时间去熟练；但步长太大，又可能使算法越过了最小值。

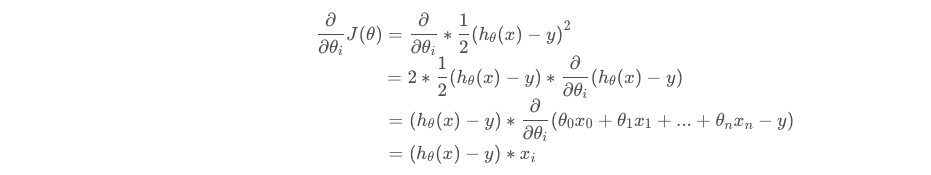
        所以，更新函数可以改为：$${\theta }_i:={\theta }_i-\alpha (h_{\theta }(x)-y)\ast x_i$$        上式是对于只有一组参数的数据进行的推导。下面是对有$m$个参数的时候的推导，也称为批梯度下降法。$${\theta }_i:={\theta }_i-\alpha \sum _{j=1}^m(h_{\theta }(x(j))-y(j))\ast x_i(j)$$

随机梯度下降法

        当参数$m$取值过大时，若直接采用梯度下降法，则迭代的次数将会变得十分庞大，因此可以采用随机梯度下降法。算法描述如下：

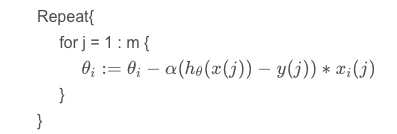
        这个算法的好处是：开始学习和修改参数时，只需要查看第一个训练样本，然后利用第一个训练样本开始更新，然后使用第二个更改后的训练样本执行下一次更新，这样使得调整参数的速度会快很多，因为不需要在调整之前遍历所有的样本数据。
        缺点是：不一定会精确的收敛到全局最小值，而是在最小值附近徘徊。

矩阵求导

        定义一个新的符号。$${\nabla }_{\theta }J=\left[\begin{array}{c}\frac{\partial J}{\partial {\theta }_0}\\ ⋮\\ \frac{\partial J}{\partial {\theta }_n}\end{array}\right]\in R^{n+1}$$        那么上述参数的时候的更新式可重写为：$$\theta :=\theta -\alpha {\nabla }_{\theta }J$$

        假设矩阵A是一个n*n的矩阵，那么矩阵A的迹，也就是矩阵A的对角元素和表示方法如下。$$\begin{gathered} IfA\in R^{n+1} \\ trA=\sum _{i=1}^n{A}_{ii} \end{gathered}$$        那么对于m*n维矩阵A，则有：$$f(A),A\in R^{m\ast n}$$$${\nabla }_{A}f(A)=\left|\begin{array}{ccc}\frac{\partial f}{\partial A_{11}}& \dots & \frac{\partial f}{\partial A_{1n}}\\ ⋮& \ddots & ⋮\\ \frac{\partial f}{\partial A_{m1}}& \cdots & \frac{\partial f}{\partial A_{mn}}\end{array}\right|$$

和迹与矩阵求导有关的关键结论

        和矩阵的转置、迹以及矩阵求导有关结论如下所示：$$\begin{gathered} trAB=trBA \\ trABC=trCAB=trBCA \\ iff(A)=trAB{\nabla }_{A}trAB=B^T \\ trA=tr{A}^T \\ ifa\in R,tra=a \\ {\nabla }_{A}trAB{A}^{T}C=CAB+C^{T}A{B}^T \end{gathered}$$

设计矩阵

        假设$x$为设计矩阵，则有：$$X\theta =\left[\begin{array}{c}{(x_1)}^T\\ {(x_2)}^T\\ ⋮\\ {(x_m)}^T\end{array}\right]\theta$$$$X\theta =\left[\begin{array}{c}{(x_1)}^T\theta \\ ⋮\\ {(x_m)}^T\theta \end{array}\right]=\left[\begin{array}{c}{h}_{\theta }(x_1)\\ ⋮\\ h_{\theta }(x_m)\end{array}\right]$$$$令\stackrel{\rightharpoonup }{y}=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right]$$        那么有：

        其中$Z{Z}^T$表示矩阵的内积，因此，令${\nabla }_{\theta }J(\theta )=0$，可以得到如下表达式：

        $y^{T}y$与$\theta$无关，所以求导为0。由前面所给出的和迹与矩阵求导有关的关键结论，可以得到下述结果，其中$I$为单位矩阵。

        所以最终$\theta$可以表示为：$$\theta ={(x^{T}x)}^{-1}{x}^{T}y$$