Problem
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a character
Solution
本来打算用LCS(最长公共子序列--可以不连续,不是最长公共子串--连续,LCS我看的他的)来解决来着,写完才发现,程序最后只有最长相同的序列,对齐即可了,那么剩余的元素,有可能元素对空(也就是添加元素)情况:
比如:
所有,最后还是换种方式来解决:
class Solution {
public:
int minDistance(string word1, string word2) {
int n1 = word1.size();
int n2 = word2.size();
if (n1 == 0 || n2 == 0) {
return max(n1, n2);
}
// vector<vector<int>> e(n1, vector<int>(n2)), diff(n1, vector<int>(n2));
vector<vector<int>> e(n1+1, vector<int>(n2+1));
for (int i = 0; i <= n1; ++i) {
e[i][0] = i;
}
for (int j = 1; j <= n2; ++j) {
e[0][j] = j;
}
for (int i = 1; i <= n1; ++i) {
for (int j = 1; j <= n2; ++j) {
e[i][j] = min(min(e[i-1][j]+1, e[i][j-1]+1), e[i-1][j-1] + (word1[i-1] == word2[j-1] ? 0 : 1));
// if (word1[i-1] == word2[j-1]) {
// diff[i][j] == 0;
// e[i][j] = min(min(e[i-1][j]+1, e[i][j-1]+1), e[i-1][j-1]);
// }
// else {
// diff[i][j] == 1;
// e[i][j] = min(min(e[i-1][j]+1, e[i][j-1]+1), e[i-1][j-1]+1);
// }
}
}
return e[n1][n2];
}
};这里,我做了优化,不用保存diff[i][j]
思路
动态规划,Edit distance问题
通过学习berkeley dynamic programming章节,然后做了leetcode这个题目,整理如下:
考虑三种情况:
x[1...i-1] <--> y[1...j] --> e[i-1][j] --> e[i][j] = e[i-1][j]+1?x[1...i] <--> y[1...j-1] --> e[i][j-1] --> e[i][j] = e[i][j-1]+1x[1....i-1] <--> y[1...j-1] --> e[i-1][j-1] + diff[i][j] --> e[i][j] = e[i-1][j-1] + diff[i][j]?
diff[i][j]:
- when x[i] == y[j], diff = 0;
- when x[i] != y[j], diff = 1;
E(i,j) = min{1+E(i−1,j), 1+E(i,j−1), diff(i,j)+E(i−1,j−1)}
结果如下:
算法:
for i = 0,1,2,...,m: E(i,0) = i
for j = 1,2,...,n: E(0,j) = j
for i = 1,2,...,m: for j = 1,2,...,n:
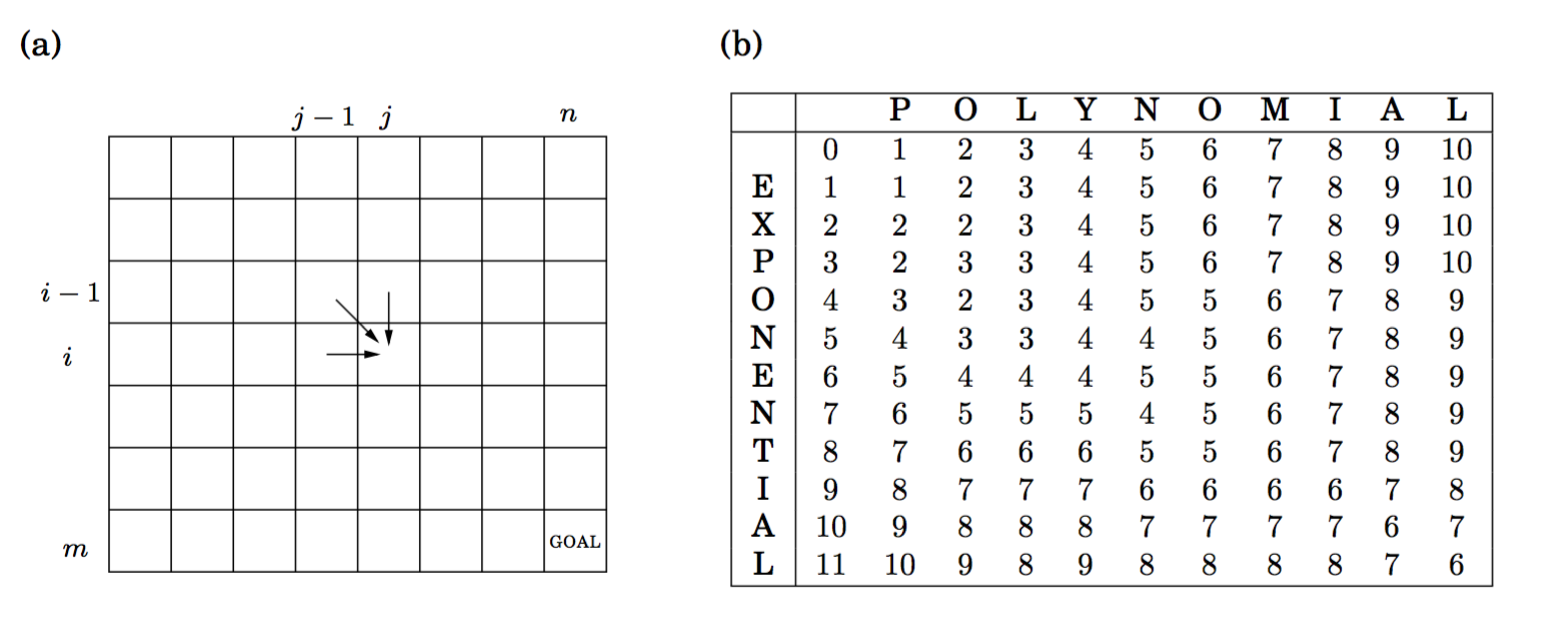
E(i, j) = min{E(i − 1, j) + 1, E(i, j − 1) + 1, E(i − 1, j − 1) + diff(i, j)} return E(m, n)算法生成矩阵:
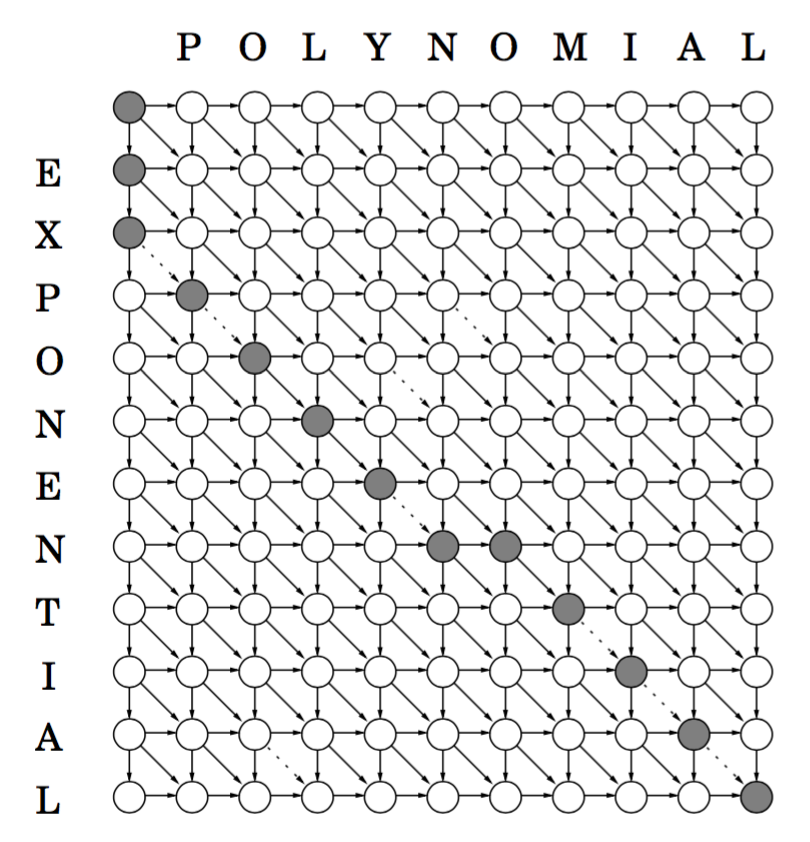
最后选择的元素(DAG)
之后,等把动态规划常见问题整理的差不多了,就做一个动态规划(DP)的总结。








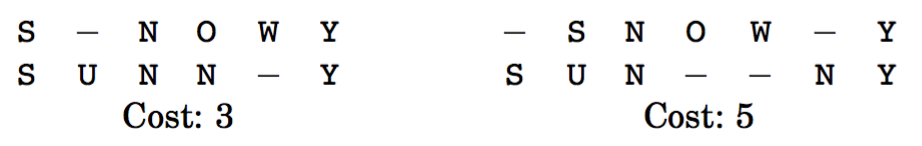
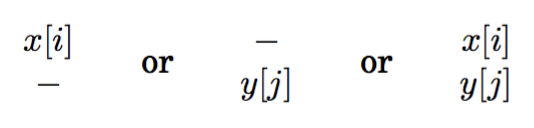
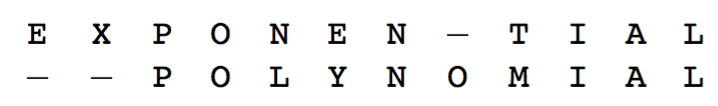














 344
344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








