【微观】十分重要的需求弹性和供给弹性

最新推荐文章于 2024-01-24 11:46:11 发布

火柴先生

最新推荐文章于 2024-01-24 11:46:11 发布

阅读量8.1k

点赞数 30

分类专栏：金融相关文章标签：微观经济学

本文链接：https://blog.csdn.net/baidu_39621090/article/details/120495790

版权

金融相关专栏收录该内容

7 篇文章

订阅专栏

弹性来表示因变量对自变量变化的反应的敏感程度。

当一个经济变量发生1%的变动时，由它引起的另一个经济变量变动的百分比。

1 弹性的一般含义

$弹性系数 = 因变量变动比例 / 自变量变动比例$

弧弹性计算公式：
$\mathrm{e}=\frac{\Delta Y / Y}{\Delta X / X}=\frac{\Delta Y}{\Delta X} \cdot \frac{X}{Y}$
当需求曲线上两点之间的变化量趋于无穷小时，需求的价格弹性要用点弹性来表示。也就是说，它表示需求曲线上某一点上的需求量变动对于价格变动的反应程度。

点弹性计算公式：

$\mathrm{e}=\lim _{\Delta \mathrm{x} \rightarrow 0} \frac{\Delta Y / Y}{\Delta X / X}=\frac{\mathrm{d} Y / Y}{d X / X}=\frac{d Y}{d X} \cdot \frac{X}{Y}$

2 需求价格弹性

一种商品价格变化1%所引起的该商品的需求量变化百分之几。
一定时期内一种商品的需求量的变动对于价格的变动的反应程度。

$需求的价格弹性系数=\frac{-需求变化率}{价格变动率}$

应用时只看大小，不看正负号。
$\mathrm{e}=\frac{\Delta Y / Y}{\Delta X / X}=\frac{\Delta Y}{\Delta X} \cdot \frac{X}{Y}$

$e_{d}=-\frac{\Delta Q / Q}{\Delta P / P}=-\frac{\Delta Q}{\Delta P} \cdot \frac{P}{Q}=-\frac{\Delta Q}{\Delta P} \cdot \frac{\frac{P_{1+} P_{2}}{2}}{\frac{Q_{1}+Q_{2}}{2}}$

在通常情况下，商品的需求量和价格是成反方向变动的。所以这里的DeltaQ/DeltaP为负值，所以为了便于比较，就在公式中加了负号。

计算涨价或降价中P和Q基数值不同，为了避免不同的计算结果带来的不便，一般取两点价格的平均值和两点需求量的平均值。（需求的价格弧弹性的中点公式）

3 需求的价格弹性的五种类型

简言之，通过刚才的公式以及图形的斜率进行把握。e>1表示需求的变化率大于价格的变化率，即对价格的反应比较敏感，所以e>1被称为富有弹性，一般竞争越激烈越有弹性。

在这里插入图片描述
在右下方倾斜的线性曲线上每一点的弹性都是不相等的。

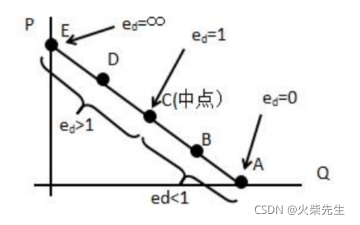
在非线性需求曲线中，直角双曲线的点弹性每点都为1。

3.1 需求的价格弹性和厂商的销售收入

	ed>1	ed=1	ed<1	ed=0	ed=∞
降价	收入增加	收入不变	收入减少	收入和价格下降同等幅度	在既定条件下，收益可以无限增加，因此厂商不会降价
涨价	收入减少	收入不变	收入增加	收入和价格上涨同等幅度	收入会减少为零

不要死记硬背，通过图形结合公式理解即可。

3.2 影响因素

商品的可替代性。一种商品的可替代品越多，该商品的需求价格弹性越大。
商品用途的广泛性。一种商品的用途越广泛，它的需求价格弹性越大。
商品对消费者生活的重要程度。生活必需品的需求价格弹性小，非必需品的需求价格弹
性大。
商品的消费支出在消费者预算总支出中所占的比重。消费者在某商铺内上的消费支出在
预算总支出中所占的比重越大，该商品的需求价格弹性就越大。

4 弹性概念的扩大

任何两个具有函数关系的经济变量之间都可以建立弹性，以研究这两个经济变量变动的相互影响。

4.1 供给的价格弹性

供给的价格弹性表示一定时期内一种商品的供给量变动对于该商品价格变动的反应程度。

4.2 ⭐️需求的交叉价格弹性

表示在一定时期内，一种商品的需求量的变动，对于它的相关商品的价格的变动的反应程度。

或者，商品Y价格变化1%引起商品X需求量变化百分之几。

$\mathrm{e}_{X Y}=\frac{\Delta Q_{X} / Q_{X}}{\Delta P_{Y} / P_{Y}}=\frac{\Delta Q_{X}}{\Delta P_{Y}} \cdot \frac{P_{Y}}{Q_{X}}=\frac{d Q_{X}}{d P_{Y}} \cdot \frac{P_{Y}}{Q_{X}}$

分类

互补品：需求交叉弹性为负值，exy<0（eg.球和球拍，P球↑，Q球↓，Q球拍↓，那么Q与P
异号，则需求交叉弹性为负）
替代品：需求交叉弹性为正值，exy>0（eg.苹果和梨，P苹果↑，Q苹果↓，Q梨↑，那么Q与P
同号，则需求交叉弹性为正）
若为零，则这两种商品之间无关系

4.3 需求收入弹性

消费者收入变化1%所引起商品需求量变化百分之几

$\mathrm{e}_y=\frac{\Delta Q / Q}{\Delta Y / Y}=\frac{\Delta Q}{\Delta Y} \cdot \frac{Y}{Q}=\frac{\mathrm{d} Q}{\mathrm{~d} Y} \cdot \frac{Y}{Q}$

分类

在这里插入图片描述

恩格尔定律

在一个家庭或一个国家中，事物支出在收入中所占的比例随着收入的增加而减少。用弹性概念来表述恩格尔定律可以是：对于一个家庭或一个国家来说，富裕程度越高，则食物支出的收入弹性就越小；反之，则越大。