本文介绍矩阵论中一对非常重要的概念:核(kernel)与象(image)。这部分内容有助于我们从更加深入的层次去审视矩阵与线性变换的关系,对于更进一步地学习和领会泛函分析中的内容也很有帮助。在阅读本文前,强烈建议读者了解前文(http://blog.csdn.net/baimafujinji/article/details/6475470)所介绍的知识。
首先,假设有一个如下所示的 n×m 的矩阵,
我们其实可以把它看成是一个函数,即(注意前文中我们已经讲过R^n表示所有n个实数数列或有序n元组的集合)
如何来理解这样一个函数呢?假设向量 x 是R^m中的一个由m个实数组成的(列)向量(m行1列),那么 Ax 根据矩阵乘法,显然就是一个由n个实数组成的(列)向量(n行1列),而 Ax 是属于R^n的。
矩阵 A 的Kernel定义为:
即
注意到 ker A 在 R^m 中。
从方程组的角度来看,ker A 也就是下面这个有n个方程的方程组的解向量的集合。
矩阵 A 的Image定义为:
也就是所有位于R^n中,可以表示成 Ax 的向量。
从方程组的角度来看,im A 也就是由下面这个方程组生成的所有的向量的集合。
或者说 im A 是 span of 矩阵 A 的列向量,即
(全文完)








 本文深入探讨了矩阵论中的核心概念——核(kernel)与象(image),通过解释它们在矩阵与线性变换之间的联系,帮助读者更好地理解这些概念,并为进一步学习泛函分析奠定基础。
本文深入探讨了矩阵论中的核心概念——核(kernel)与象(image),通过解释它们在矩阵与线性变换之间的联系,帮助读者更好地理解这些概念,并为进一步学习泛函分析奠定基础。

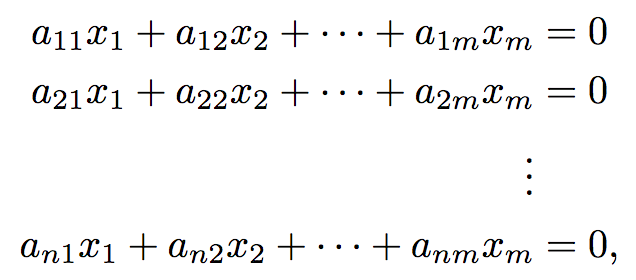
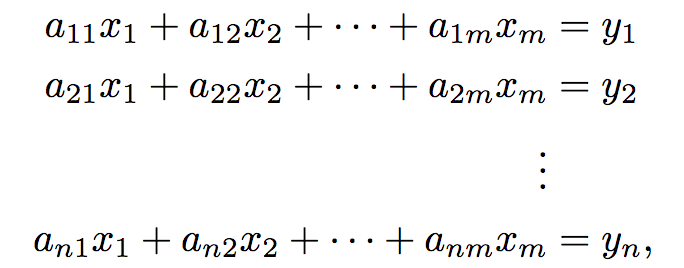
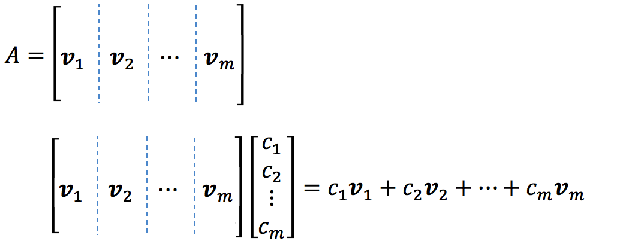

















 6016
6016

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










