约束复原与维纳滤波（数学原理与MATLAB实现）

在【图像处理中的数学原理】专栏（该专栏中的文章已经结集出版，书名为《图像处理中的数学修炼》）之前的一篇文章中，我们曾经讨论过一种“自适应图像降噪滤波器的设计与实现”。彼时，也曾经提过其中运用了维纳滤波器的一些方法，但我们并未深入讨论关于维纳滤波的更多内容。本文作为这个系列中的一个续篇，继续来深入研究著名的维纳滤波，特别是其背后的数学原理。这也涉及到了限制性图像复原和非限制性图像复原的一些话题。

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。

---

图像复原的逆滤波方法

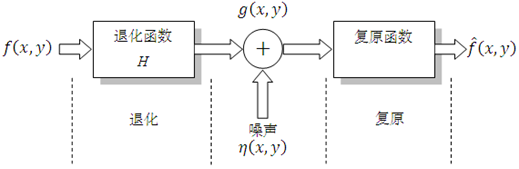
如果$H$是一个线性移不变系统，那么在时域中给出的退化过程可由如下公式给出：$$g(x,y)=h(x,y)\ast f(x,y)+\eta (x,y)$$其中，$h(x,y)$是退化函数在时域下的表示，运算符$\ast$表示时域卷积。由卷积定理可知，时域上的卷积等同于频域上的乘积，所以上式在频域中的表述如下：$$G(u,v)=H(u,v)F(u,v)+N(u,v)$$其中的大写字母项是之前公式里对应项的傅里叶变换。退化函数$H$通常是指模糊、抖动等影响。

如果认为噪声的影响很小，那么上面的式子就可以写成 $G(u,v)=H(u,v)F(u,v)$，假设 $H(u,v)$是可逆的，那便可以得出 $F(u,v)=G(u,v)/H(u,v)$。但实际上噪声是在所难免的，因而只能设法求出 $F(u,v)$的估计值 $\hat{F}(u,v)$，此时用 $H(u,v)F(u,v)+N(u,v)$来替换 $G(u,v)$，则有： $$\hat{F}(u,v)=\frac{H(u,v)F(u,v)+N(u,v)}{H(u,v)}=F(u,v)+\frac{N(u,v)}{H(u,v)}$$
这也就是逆滤波（inverse filter）的基本原理。从这个公式可以看出：首先，如果希望复原后的 $\hat{F}(u,v)$与 $F(u,v)$尽量接近，就需要 $\min ||N(u,v)||$；其次，如果噪声比较大，特别是噪声的影响大过退化函数的影响，那么复原的效果就会很差。

不妨在MATLAB中做一些简单的实验。在后面我们实现了一个用于图像复原的维纳滤波函数mydeconvwr(I, PSF, NSR)，其中I是待处理的退化图像，PSF是退化函数（以矩阵形式给出），当NSR=0时，这个函数就变成了一个逆滤波器。下面来实验一下，不加任何噪声的情况下调用mydeconvwr函数来对图像进行复原。

I = im2double(imread('cameraman.tif'));
LEN = 21; THETA = 11;
PSF = fspecial('motion', LEN, THETA);
blurred = imfilter(I, PSF, 'conv', 'circular');

result1 = mydeconvwnr(blurred, PSF, 0);

subplot(1,3,1),imshow(I),title('original image');
subplot(1,3,2),imshow(blurred),title('blurred image');
subplot(1,3,3),imshow(result1),title('restored image');

执行上述代码，所得之结果如下图所示。可见在不引入噪声的情况下，逆滤波的图像复原效果非常好。

下面我们试着向退化的图像中加入一些高斯噪声，然后再用逆滤波来对图像进行复原，实验代码如下。

noise_mean = 0;
noise_var = 0.0001;
blurred_noisy = imnoise(blurred, 'gaussian', noise_mean, noise_var);
estimated_nsr = 0;
result2 = mydeconvwnr(blurred_noisy, PSF, estimated_nsr);
subplot(1,2,1),imshow(blurred_noisy ),title('blurred image with noise');
subplot(1,2,2),imshow(result2),title('resotred image without considering noise');

执行上述代码，所得之结果如下图所示。可见在引入噪声的情况下，逆滤波的图像复原效果非常不理想。

---

在MATLAB中实现维纳滤波

维纳滤波的基本公式是$$\hat{F}(u,v)=[\frac{H^{\ast }(u,v)}{|H(u,v){|}^2+P_N(u,v)/P_S(u,v)}]G(u,v)=[\frac{1}{H(u,v)}\cdot \frac{|H(u,v){|}^2}{|H(u,v){|}^2+P_N(u,v)/P_S(u,v)}]G(u,v)$$其中$H(u,v)$表示退化函数，$H(u,v{)}^2=H^{\ast }(u,v)H(u,v)$，$H^{\ast }(u,v)$表示$H(u,v)$的复共轭；$P_N(u,v)=|N(u,v){|}^2$表示噪声的功率谱；$P_S(u,v)=|F(u,v){|}^2$表示原图像的功率谱；比率$P_N(u,v)/P_S(u,v)$称为信噪比。当无噪声时，$P_N(u,v)=0$，则维纳滤波退化为逆滤波（又称为理想的逆滤波器）。所以，逆滤波也可以认为是维纳滤波的一种特殊情况。而且，没有噪声情况下的逆滤波中$N(u,v)/H(u,v)=0$，逆滤波可以很正常对退化图像进行复原。

但是在实际应用中，$P_N(u,v)/P_S(u,v)$通常是未知的，当然我们也可以设计很多方法来估计$P_N(u,v)$，因为噪声信息就位于$G$中，而$G$是已知的。但是$P_S(u,v)$确实无法估计的，因为$F$是未知的（而且也正是要求解的）。因此通常的做法是会采用一个常数值$k$来代替$P_N(u,v)/P_S(u,v)$。这时$k$就变成了一个可以调节的参数，于是维纳滤波的公式又可以写成：$$\hat{F}(u,v)=[\frac{1}{H(u,v)}\cdot \frac{|H(u,v){|}^2}{|H(u,v){|}^2+k}]G(u,v)$$
下面我们来分析一下维纳滤波器是如何改进和弥补逆滤波之不足的。逆滤波的问题在于$F$和$\hat{F}$之间差了一个$N/H$。（相对于N而言）$H$特别小或者（相对于$H$而言）$N$特别大都会导致$N/H$这一项变得很大，而使得$F$和$\hat{F}$之间的差距增大。但是在维纳滤波中，一个比较直观的理解是，当$H$ 特别小但$N$ 特别大的时候，上式括号中乘法运算的第一项会变大，但是第二项却会变小，这一两项之间的乘积仍然会维持在一个适中的范围（而不会变得特别大）。这也就是对维纳滤波的一个比较直观的解释，当然本文后面还会从数学角度来推导它的合理性。但在此之前，还是先在MATLAB中检验一下维纳滤波的能力。

下面的代码实现了基于维纳滤波的反卷积图像复原算法，这个代码的最初版本来自MATLAB的内置函数deconvwnr，笔者进行了修改，使其更适合用于算法演示，这个算法是完全遵照之前给出之维纳滤波公式来实现的。

function J = mydeconvwnr(I, PSF, NSR)
%   deconvolves image I using the Wiener filter algorithm, 
%   returning deblurred image J. Image I can be an N-dimensional array. 
%   PSF is the point-spread function with which I was convolved. 
%   NSR is the noise-to-signal power ratio of the additive noise. 
%   NSR can be a scalar or a spectral-domain array of the same size as I. 

% Compute H so that it has the same size as I.
% psf2otf computes the FFT of the PSF array
% and creates the OTF(optical transfer function) array. 
sizeI = size(I);
H = psf2otf(PSF, sizeI);

S_u = NSR;
S_x = 1;

% Compute the Wiener restoration filter:
%
%                   H*(k,l)
% G(k,l)  =  ------------------------------
%            |H(k,l)|^2 + S_u(k,l)/S_x(k,l)
%
% where S_x is the signal power spectrum and S_u is the noise power
% spectrum.
%
% To minimize issues associated with divisions, the equation form actually
% implemented here is this:
%
%                   H*(k,l) S_x(k,l)
% G(k,l)  =  ------------------------------
%            |H(k,l)|^2 S_x(k,l) + S_u(k,l)
%

% Compute the denominator of G in pieces.
denom = abs(H).^2;
denom = denom .* S_x;
denom = denom + S_u;
clear S_u

% Make sure that denominator is not 0 anywhere.  Note that denom at this
% point is nonnegative, so we can just add a small term without fearing a
% cancellation with a negative number in denom.
denom = max(denom, sqrt(eps));

G = conj(H) .* S_x;
clear H S_x
G = G ./ denom;
clear denom

% Apply the filter G in the frequency domain.
J = ifftn(G .* fftn(I));
clear G

J = real(J);

下面的代码调用了上述函数，并演示了对含有噪声的退化图像进行复原的效果。特别地，这里我们采用了两个SNR的估计方法，其中之一就是简单地根据经验值来估测一个值（当然事实上这种方法要经过调参才会得到较好的效果）。

estimated_nsr = 0.001;
result3 = mydeconvwnr(blurred_noisy, PSF, estimated_nsr);
estimated_nsr = noise_var/var(I(:));
result4 = mydeconvwnr(blurred_noisy, PSF, estimated_nsr);
subplot(1,2,1),imshow(result3),title('restored image with estimated nsr(1)');
subplot(1,2,2),imshow(result4),title('restored image with estimated nsr(2)');

从下面的执行结果图来看，维纳滤波的复原效果确实已经使得图片可以辨识，这一点上较之前的逆滤波来说效果的改进是显而易见的。

---

限制性图像复原与维纳滤波的数学推导

如果你能坚持住一直看到这里，那么其实你对维纳滤波已经建立起来了一个很具体的认识了。如果你对背后的数学原理并不太关心，或者数学基础较差，那么建议你跳过这个部分。如果你很感兴趣但是阅读的时候仍然有较大的障碍，那么我建议你翻看《数字图像处理原理与实践（MATLAB版）》的11.2.1小节，以弥补自己在必备基础上的缺失。

图像复原的方法较多，按大类可分为无约束复原和有约束复原（或称约束复原）两种，即无约束复原和有约束复原（constraint restoration）。无约束恢复是一种在图像恢复过程中不受其他条件限制的一种方法。典型方法是逆滤波法。此外，在图像恢复过程中，为了在数学上更容易处理，常常给复原加上一定的约束条件，并在这些条件下使某个准则函数最小化。这类方法叫做有约束恢复，其中典型的方法有维纳滤波法和约束最小平方滤波法。

无约束恢复是一种在图像恢复过程中不受其他条件限制的一种方法。在对 $n$ 没有先验知识的情况下，需要寻找一个$f$ 的估计$\hat{f}$ ，使得$H\hat{f}$在最小均方误差的意义下最接近$g$ ，即要使 $n$ 的范数最小。即$$||n|{|}^2=n^{T}n=||g-H\hat{f}|{|}^2=(g-H\hat{f})(g-H\hat{f})$$最小化上式则可以推出：$$\hat{f}=H^{-1}g$$上式中的结果就是无约束恢复在空域中的表达式，由此也就得到了本文最开始介绍的逆滤波。

现在换一种思考方式，为了在数学上更加灵活地处理，我们给优化问题加上一个约束条件，如果你在数学上足够敏感，应该马上就能想到：YES，接下来就要使用拉格朗日乘数法了！

现在的问题是要找到原图像$f(x,y)$的一个估计值$\hat{f}(x,y)$，使得估计值与原图像之间的均方误差在统计意义上最小。即满足： e 2 = E { [ f ( x , y ) − f ^ ( x , y ) ] 2 } e^2=E\{[f(x,y)-\hat f(x,y)]^2\} e2=E{[f(x,y)−f^​(x,y)]2}在无约束图像复原中，我们要进行最优化的目标函数是$||g-H\hat{f}|{|}^2=||n|{|}^2$，现在把这个目标函数看成是约束条件，转而构造一个新的目标函数$||Q\hat{f}|{|}^2$，其中$Q$是一个linear operator on $f$。注意因为，这个目标函数是我们构造的，所以约束复原的灵活性就在于我们可以指定$Q$，当$Q$取不同值的时候，我们就会得到不同的解，例如，后面便会揭晓在维纳滤波中我们是如何设计$Q$的样子的。所以总结一下现在的问题是：$$\min ||Q\hat{f}|{|}^2,s.t.||g-H\hat{f}|{|}^2=||n|{|}^2$$
遇到带约束条件的最优化问题，遂采样拉格朗日乘数法，即$$J(\hat{f})=||Q\hat{f}|{|}^2+\alpha (||g-H\hat{f}|{|}^2-||n|{|}^2)$$接下来按照最优化的一般方法，将上式对$f$求导并令导数等于0。所以有$$\frac{\partial J(\hat{f})}{\partial \hat{f}}=0=2Q^{T}Q\hat{f}-2\alpha H^T(g-H\hat{f})$$进而有$$\hat{f}=(H^{T}H+\gamma Q^{T}Q{)}^{-1}{H}^{T}g,where\gamma =\frac{1}{\alpha }$$至此，已经可以看到约束性复原和非约束复原在计算$\hat{f}$时的差异了。现在问题就在于该如何构造$Q$。

维纳滤波法是一种统计方法，是建立在图像和噪声都是随机过程，图像和噪声不相关的基础上，由此得到的结果在图像统计平均意义下是最优的。那么如何体现“图像和噪声都是独立的不相关的随机过程”这一意义呢？对于$f$和$n$，分别构造它们的相关矩阵（correlation matrix）$R_f$和$R_n$，即 R f = E { f f T } R_f=E\{ff^T\} Rf​=E{ffT}， R n E { n n T } R_nE\{nn^T\} Rn​E{nnT}，注意如果这里向量$f$和$n$的大小都是n，那么$R_f$和$R_n$的大小就是n×n。$R_f$的第$ij$个元素是 E { f i f j } E\{f_if_j\} E{fi​fj​}，代表$f$的第$i$个和第$j$个元素的相关系数（同理对于$R_n$中的元素也有类似的表达式）。因为$f$和$n$中元素全部都是实数，所以$R_f$和$R_n$都是实对称矩阵。

对于大多数图像而言，像素间的相关性都与像素的相对距离有关。通常在一幅图像中，如果两个像素相距离较远，那么它们的相关性就较低（相关系数趋于0），相反如果两个像素位置上比较接近，那么它们的相关性较大（相关系数趋于1），所以可以想象$R_f$和$R_n$的样子将近似于一个对角线矩阵（近似的意思是对角线上的值都为1，接近对角线的位置元素值接近1，其它上下三角的位置元素值基本都为0）。

根据“两个像素间的相关性只是它们彼此之间相互距离的函数而非相对位置的函数”这一假设，可以将$R_f$和$R_n$都用块循环矩阵来表示，则有$R_f=WA{W}^{-1}$，其中$W$是$R_f$的特征向量组成的矩阵，$A$中的元素对应$R_f$中相关元素的傅里叶变换。同理，亦有$R_n=WB{W}^{-1}$，其中$W$是$R_n$的特征向量组成的矩阵，$B$中的元素对应$R_n$中相关元素的傅里叶变换。这些相关元素的傅里叶变换称为图像和噪声的功率谱。注意，这里面其实用到了一个非常重要的结论，即任意循环矩阵可以被傅里叶变换矩阵对角化。这个方法在图像处理及计算机视觉研究中是一种十分常用的加快算法计算速度的技术，例如2015年发表于TPAMI的文献【3】。但限于篇幅这里无法对循环矩阵的傅里叶对角化方法进行更为详细的介绍，如果读者对此不甚了解，可以参考文献【2】中指定的篇幅或者文献【4】。

现在我们可以来指定$Q$的选择方法了，令$Q^{T}Q=R_f^{-1}{R}_n$，则有（注意$H$可以写成$H=WD{W}^{-1}$，其中$D$是对角矩阵，其元素正是$H$的特征值，关于$D$的更多解释同样请参考文献【2】）：$$\hat{f}=(H^{T}H+\gamma Q^{T}Q{)}^{-1}{H}^{T}g=(W{D}^{\ast }D{W}^{-1}+\gamma W{A}^{-1}B{W}^{-1}{)}^{-1}W{D}^{\ast }{W}^{-1}g$$由此可得：$$W^{-1}\hat{f}=(D^{\ast }D+\gamma A^{-1}B{)}^{-1}{D}^{\ast }{W}^{-1}g$$进行变量的等价替换便得到：$$\hat{F}(u,v)=[\frac{H^{\ast }(u,v)}{|H(u,v){|}^2+\gamma \frac{P_N(u,v)}{P_S(u,v)}}]G(u,v)=[\frac{1}{H(u,v)}\cdot \frac{|H(u,v){|}^2}{|H(u,v){|}^2+\gamma \frac{P_N(u,v)}{P_S(u,v)}}]G(u,v)$$特别地，当$\gamma =1$时，上式中括号里的部分就称为维纳滤波器，当$\gamma$为变参数时，则称为变参数维纳滤波器。

维纳滤波法是一种统计方法，是建立在图像和噪声都是随机过程，图像和噪声不相关的基础上，由此得到的结果在图像统计平均意义下是最优的，但对某一具体图像来说不一定是最优的。另外，用维纳滤波器的另一个困难是要求知道噪声和未退化图像的功率谱，而这在实际中是难以达到的，只能用某个常数代替，从而造成误差。

---

推荐阅读与参考文献

【1】 本文中的内容主要来自《数字图像处理原理与实践（MATLAB版）》，电子工业出版社，如果你对维纳滤波的数学推导仍然不能完全理解，建议你参考P391~P397.
【2】 同时推荐IIT的Prof. Sengupta的数字图像处理公开课（需要自备梯子）.
【3】 Henriques, João F., et al. “High-speed tracking with kernelized correlation filters.” IEEE Transactions on Pattern Analysis and Machine Intelligence, 37.3 (2015): 583-596.
【4】 循环矩阵傅里叶对角化. （最后浏览时间2017年6月）