有趣的数学 完美钻石切工的数学

钻石切割的历史

        毛坯钻石通常看起来像旧玻璃片，只有经过切割和抛光后，它们才开始呈现出美丽的外观。即使是迄今为止发现的最大的钻石原石（被称为库里南钻石），在被切割成单颗钻石（其中一些被用于制作皇冠上的宝石）之前，它看起来也不起眼。

        自中世纪以来，人们就开始切割钻石，随着时间的推移，形状不断演变，生产出越来越有吸引力的钻石。到 1900 年，古老的欧洲切工已成为最流行的设计之一，它类似于我们所认为的现代钻石。

        大约在这个时候，钻石切割工具不断改进，钻石切割师可以使用新的珠宝锯和车床。这意味着现在可以研究是否存在理论上完美的钻石切工，因为工具精度不够不再是主要限制。

1900 年之前金刚石切割的演变

寻找完美的切工

        接受挑战寻找完美切割钻石的年轻人叫做Marcel Tolkowsky。他非常适合研究钻石切割，因为他的家庭是一个世代切割钻石的工匠世家，而且还在伦敦大学工程学院攻读博士学位。Tolkowsky的博士论文专注于钻石的研磨和抛光，这意味着他能够利用自己的数学和科学知识，并将其应用于寻找钻石最佳切割方法的问题。

亮度与火彩

        人们在钻石上寻找的主要品质有两个。第一个是亮度——这是衡量观看钻石的人反射回多少光的指标。如果光线进入钻石，然后直接离开钻石背面，那么它就会显得沉闷而无生气。另一种性质被称为火彩——这是白光分散成彩虹色的组成部分。亮度和火彩的结合产生了我们都知道和喜爱的闪闪发光的效果。

折射

        Marcel Tolkowsky观察了光线进入不同切割钻石时的行为。当光线从空气进入钻石等材料时，它会改变方向，这一过程被称为折射。

        材料的折射率可以计算如下：

        折射率 = 空气或真空中的光速 / 材料中的光速

        与折射率为1.52的普通玻璃相比，金刚石具有2.42的极高折射率。钻石是所有天然材料中折射率最高的材料之一，这也是它如此特殊的原因之一。

        当你增加光线的角度时，它最终会达到所谓的临界角。这意味着光将停止折射，而是被反射。钻石的临界角约为24度，而玻璃的临界角则约为41度。

光线从玻璃传播到空气时的临界角示意图

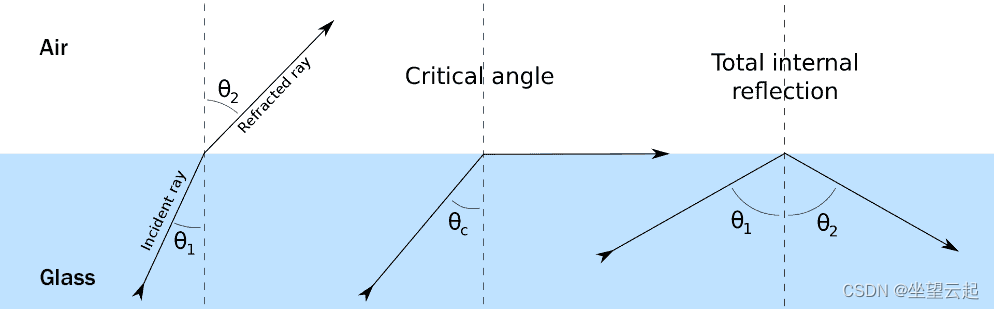
        托尔科夫斯基利用这些知识来检测，他想设计一种钻石，使光线以大于临界角的角度进入并照射背面，最初产生内部反射。然后，他希望光线以小于临界角的角度照射到钻石的顶面，从而折射出钻石的顶部，到达观看钻石的人的眼睛。托尔科夫斯基发现，大多数钻石切割得要么太深，要么太浅。

箭头表示光线穿过钻石的路径，中间的图示为理想的切割

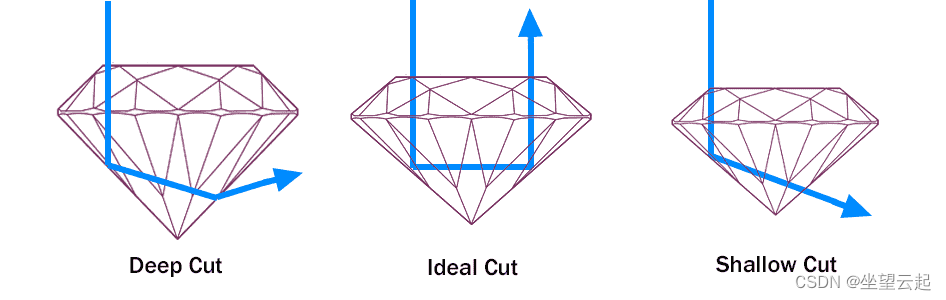
        他利用几何学得出了所谓的理想钻石切割。这是为了优化亮度和火焰，许多现代钻石都是基于托尔科夫斯基的原始设计。类似的理论可以用于优化其他宝石的切割，使用它们各自的临界角。

用数学切割钻石

        钻石切割机还面临着充分利用原石和避免浪费的问题。经验丰富的钻石切割工预计只需使用三分之一的原石就可以生产出成品钻石，考虑到钻石的昂贵程度，这是一种巨大的浪费。

        Fraunhofer研究所的数学家一直在研究如何提高经验丰富的刀具的判断能力。他们使用了一种被称为“半无限优化”的数学技术，他们的算法使产量增加了约10%。这听起来可能没有那么多，但考虑到钻石的成本，这是一个显著的改进。