故障树手册（Fault Tree handbook)（6）

第十章 概率与统计分析

1 概述

在这章中，我们将试图去描述和故障树相关的概率与统计概念中的基本元素。这些知识也是故障树量化的基础。在这方面基础好的读者可以直接跳过本章去阅读第十一章，在后边需要的时候再来回顾对应的内容。

我们现在先来讨论概率分布理论。我们首先会讲解二项分布，接着学习常规的分布原理，并重点学习一些在系统分析中常用到的特殊分布。然后我们将具备统计评估的基础知识。

我们的表示法或许不是最好的传统数学统计，我们的方法是一个作者在对工程学的学生和工程师统计课程的过程中所采用的改进后的方法。我们有时会为了更好更快的阐述概念而牺牲一些数学的严谨性。

2 二项分布

假设我们有四个相似的系统，这些系统都经过特定时间的测试。在测试的最后我们进一步的假设所有的测试结果我们都准确的以“成功”或“失败”进行了记录。如果成功的概率用p来表示（失败的概率就是1-p），那么在四次实验外的成功的概率是多少？

这个实验的结果集合可以用如下表示（下标表示第几次实验，S表示成功，F表示失败）：

$S_1{F}_2{S}_3{F}_4$表示“第一次沈工，第二次失败，第三次成功，第四次失败”。该结果的概率为$p\cdot (1-p)\cdot p\cdot (1-p)=p^2\cdot (1-p{)}^2$。注意在这四次实验中，四次都成功的方法只有1种，三次成功一次失败的方式有四种，两次成功两次失败的方式有6种，一次成功三次失败的方式有四种，全部失败的方式有一种。总的来说，对于n次实验，其中成功x次的方式为
$$C_x^n=\frac{n!}{x!(n-x)!}$$
它其实就是n个物体一次拿出x个的组合的数量。注意一共有$2^4=16$个不同的结果。如果实验n次，每次结果要么是“成功”要么是“失败”，那么就应该会有$2^n$个结果。

让我们按照如下的方式进行分类：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6VWT3guE-1586708457762)(asserts/figureX-t2.png)]

考虑最后一列的各项。$4p^3(1-p)$表示四次实验中有3次成功的概率。四次实验中成功三次可以有四种方式，如果有3次成功，那么我们一定有一次失败。三次成功一次失败的概率是$p^3(1-p)$，因为有四种结果方式，因此最终的概率是$4p^3(1-p)$。最后一列的表达式表示二项分布的单独项，它的标准形式如下所示：

如果任意实验的成功概率是p，那么
$$P[n实验成功x次]=C_n^x{p}^x(1-p{)}^{n-x}=b(x;n,p)\text{\hspace{1em}(X-1)}$$

$b(x;n,p)$表示概率密度形式的二项分布。概率密度形式会在后边的章节进行讨论。如果读者让n=4，且x的取值范围是0到4，将能看到从公式X-1中得到的前一个例子的概率列中的单独项。

在n次实验中最多获得X成功的概率，以及最少获得X项成功的概率，可以通过将对应的单独项相加来获得。

$$P[n次实验最多成功x次]=\sum _{s=0}^x{C}_n^s{P}^s(1-p{)}^{n-s}\equiv B(x;n,p)\text{\hspace{1em}(X-2)}$$

$$P[n次实验最少成功x次]=\sum _{s=x}^n{C}_n^s{p}^s(1-p{)}^{n-s}=1-\sum _{s=0}^{x-1}{C}_n^s{P}^s(1-p{)}^{n-s}\text{\hspace{1em}(X-3)}$$

其中，B(n;n,p)是累积分布形式里的二项分布（累积分布将会在后一个章节讨论）。在这个阶段，我们可以简单的解释二项式是成功次数小于等于某个值的概率。因此，回到我们的例子，四次实验中成功两次的概率是：

$$6p^2(1-p{)}^{+}4p^3(1-p)+p^4=1-[(1-p{)}^4+4p(1-p{)}^3]$$

二项分布是一个非常大的表格，经常是公式X-2的形式但有时候会是公式X-3的形式，有时候是X-1的形式。可以查看参考资料【1】，【33】，【41】中的例子。

二项分布的统计平均值是np，方差是$np(1-p)$。平均值是分布位置的度量，而方差是分散程度的度量。这些知识会在随后的章节中讨论。

在使用二项式的过程中，我们已经做出了很多的假设。明确的列出这些假设非常重要。

1. 每一次实验都有且只有两个实验结果。我们可以用“正常”“故障”来表示结果，也可以用其他的方式准确表示。
2. 一共有n次随机试验，n是已经确定的数字。
3. 所有n次实验完全独立。
4. 成功的概率可以用p或者其他字母表示，p在实验的过程中是一个不变的常数。

非常重要的一点是，如果问题出现，并违反了上边一条或多条的假设，那么使用二项分布就是有疑问的，除非对违反的效果进行调查。事实上，所有的分布和所有的数学方程的特征都是基于一些假设和限制的，使用这些分布或方程涉及到这些假设和限制的相关方面。

现在让我们重新审视这些假设，假如说其中某一条假设并不成立，那么我们能做什么？我们来看几个违反这些假设的例子。

1. 如果实验的结果不止一个会怎样？在某些测试方法中，会有三个可能的决策：接受批次，拒绝批次，继续实验。如果我们从装有白色、绿色、红色、黄色、蓝色芯片的容器内抽取一个芯片，每一次的实验结果会有5种可能性。这种案例不会构成严重问题，我们简单的用二项分布的扩展方法来取代二项分布，这个方法就是多项分布，该方法在很多统计著作中都有讲到（例如参考资料52）。如果适用，我们也可以将结果分类为“成功”与“失败”，并在更粗略的分类上使用二项式。（在这里“成功”的概率是所有归类为成功的事件的概率的和）

2. 现在我们假设实验的次数n是未知的，但是知道成功的次数。例如，我们扔一个骰子直到扔出一个5.我们并不能事先知道我们要抛多少次。或者，我们可以去测试相似的继电器直到发现一个坏的，同样的，我们不知道需要测试多少次。在这种情况下，我们不能使用二项式，但是另一个和二项分布相关的分布是可以用的，它叫做“负二项分布”（参考资料13）。负二项分布$\hat{b}(x;k,p)$给出了进行到x个实验时第k次成功的概率。
   $$\hat{b}(x;b,p)=C_{x-1}^{k-1}{p}^k(1-p{)}^{x-k}\text{\hspace{1em}(X-4)}$$

3. 如果n次实验的结果是互相依存的（例如第x+1次的结果依赖于前x次的结果或可能与前面的结果有关），困难就会增加好多。需要各种条件概率表示。特定结果顺序概率依赖于发生的次序,每个不同的次序有不同的概率。举个例子，用二项分布来估计是否会下雨就是不可行的事情，因为天气模式一般会持续几天或几周，星期三是什么天气与星期二是什么天气有关。如果独立性存疑，则应该先进行独立性检查在应用二项分布解决问题（参考资料11）。

4. 如果成功的概率在实验的进行过程中发生了变化，当实验的样本选自一个固定的范围且不拿出替换，这时我们能用超几何分布（hypergeometric distribution)解决该问题。这个分布的形式如下：
   $$h(x;n,a,b)=\frac{C_a^x{C}_b^{n-x}}{C_{a+b}^n}\text{\hspace{1em}(X-5)}$$

其中，a是总体中具有特征A的项目数量，b是总体中具有特征B的项目数量，N=（a+b)是总体或批次的大小，n是从总体中抽取样本的大小，x是样本中具有特征A的数量。

举个例子，特征A是有缺陷的，特征B是没有缺陷的。$h(x;n,a,b)$得出恰好n样本中有x个具备特征A的概率。

当从一个小数量总体中进行抽样且不替换时，必须应用超几何分布。（”小“表示N和n在数量上是同一级别的）。举个例子，如果我们接受了50个电感，其中10个有缺陷，那么有问题的部分就有五分之一，但是当我们抽取20个样本而不替换时，该比例会发生变化。

从公式X-5我们可以看出，使用超几何分布涉及到包含阶乘在内的复杂的计算，因为这个原因，二项式经常在此类问题中使用以获得近似的结果。二项分布能在$N\ge 10n$（其中N是总体数量,n是抽样数量，一些作者认为这里应该是$N\ge 8n$）时获得近似结果。在此类问题中，$a/n$近似等于$p$。

一个应用二项分布的特殊例子，考虑如下的问题，ABC公司大量生产一个型号的电阻。以前的经验表明电阻的缺陷率是百分之一。因此，一个采样的缺陷概率$p=0.01$。如果从生产线上一次采样10个电阻，那么其中只有一个缺陷电阻的概率是多少？我们可以得出

$$\begin{gathered} x=1,n=10,p=0.01 \\ b(x=1;n=10,p=0.01)=C_{10}^1\times 0.01\times 0.99^9 \end{gathered}$$

如果二项式分布表可用，我们就可以简单的通过寻找B(1)-B(0)来评估，因为

$$\begin{array}{rl}& B(1)=P[0或1个缺陷电阻]\\ & B(0)=P[只有0个缺陷电阻]\\ & B(1)-B(0)=0.9957-0.9044=0.0913\end{array}$$

为了日后相似的计算，我们可以画一张10个抽样中含有$x=0,1,2,3..10$个故障电阻的概率的分布函数。该分布如图X-1所示，图X-1的曲线并不是十分合理，因为二项分布是离散的，但是这样连续插值可以更好的显示出分布的总体形状。

在可靠性和安全性评估中，如果每一个每一个冗余部件工作独立，且每个冗余部件都有（近似）同样的失效概率，那么二项分布是适用于该冗余系统的。举个例子，假设我们有一个n冗余部件，假设其中多于x个发生故障，则系统就会故障。该系统不发生故障的概率就是小于等于x个部件故障的概率，这正是二项累积概率$B(x;n,p)$。

或者，假设有一种情况中有n个可能发生的事件，倘若多于x件事情发生，则出现灾难。如果n件事情互相独立且发生概率相同。那么二项分布就是适用的。总的来说，当某事件重复n次，我们想直到其中某个结果出现x次，小于x次或者大于x次的概率时，二项分布就是适用的。这里的“n次实验“可以是n个部件，n年，n个系统或者其他适用的数量单位。

我们将短暂的返回二项分布，因为它的两个限制形式对我们很重要。我们将对其分布和分布参数进行讨论研究。

3. 累积分布函数（Cumulative Distribution Function)

让我们用X代表随机实验的可能结果。X经常用来表示随机变量，这个值可能会是离散（比如一个批次里边的数量）的或者连续的（比如重量，高度）。事实上，即使表面上是连续的变量，由于存在测量的分辨率，看起来连续的值也是一个离散变量。将这些量看成是连续的会让数学层面方便一些。用对应的小写字母x来表示一个随机量会更方便一些。

在这里我们需要展现的基本公式将以连续值的形式给出，在需要给出连续值与离散值的不同的地方，我们会加以说明。总的来说，在操作上是用求和富豪来代替整数符号的问题。在累积分布方程中用于表示概率形式的$F(x)$里，我们一般表示X的值要小于等于x的值。

$$F(x)=P[X\le x]\text{\hspace{1em}(X-6)}$$

根据公式X-6，因为F(x)是个概率，因此

$$0\le F(x)\le 1$$

如果X的取值范围是负无穷到正无穷，那么

$$\begin{gathered} F(-\infty )=0 \\ F(+\infty )=1 \end{gathered}$$

如果X有更小的限定$x_1<X<x_u$，那么

$$\begin{gathered} F(x_1)=0 \\ F(x_u)=1 \end{gathered}$$

F(x)有个很重要的性质是随着x的增加，它的值是不会减小的。在严格的数学含义上，它是一个非减函数，但是不一定单调。它可以更简洁的表示如下：

If$x_2>x_1$, then$F(x_2)\ge F(x_1)$

一个更重要的性质如公式X-7所示：
$$P[x_1\le X\le x_2]=F(x_2)-F(x_1)\text{\hspace{1em}(X-7)}$$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oqkWE3Xc-1586708457765)(asserts/figureX-2.png)]

我们在第二节遇到的二项累积分布B(x;n,p)是F(x)一种特殊形式。F(x)连续和离散变量的标准形式如图X-2所示。

我们展现在上边方程中的累积分布函数的性质对离散和连续随机变量是有效的。

举一个随机变量和对应的累积分布的例子，在一个随机试验中，我们观察一个单独的器件的故障次数。每当该部件故障，我们就修好它，将时间t归0，并记录下次故障的时间。

我们假设维修并不会改变部件故有性质，也就是说每次维修都会让部件回到初始状态。随机变量T是初始化或维修后到发生故障的时间。我们用$t_i$来表示T的特定值。累积分布$F(t)$用来表示任意给定故障时间少于或等于t的概率。

另一个例子，我们针对某样物体进行反复的测量。随机变量X表示测量结果，$x_i$表示某次测量结果。累积分布F(x)表示测量值小于或者等于x的概率。我们能从$F_{est}(x_i)$来估计$F(x)$，其中
$$F_{est}(x_i)=\frac{n_i}{n}$$

n是测量的总次数，$n_i$是测量的X小于等于$x_i$的测量次数，随着n不断的变大，$F_{est}(x_i)$也在不断的接近$F(x_i)$。在应用中，累积分布函数必须根据理论思考来确定，或者通过统计方法估算。

4. 概率密度函数(probability Density Function)

对于连续随机变量，概率密度函数(probablity desity function,简称pdf),f(x)，可以通过F(x)微分的方式获取。

$$f(x)=\frac{d}{dx}F(x)\text{\hspace{1em}(X-8)}$$

它的等效形式是

$$F(x)={\int }_{-\infty }^{x}f(y)dy\text{\hspace{1em}(X-9)}$$

因为f(x)是非递减函数的斜率，我们有

$$f(x)\ge 0\text{\hspace{1em}(X-10)}$$

若概率函数在整个范围内进行积分，那么结果是统一的。

$${\int }_{-\infty }^{\infty }f(x)d(x)=1\text{\hspace{1em}(X-11)}$$

$f(x)$的性质使得我们可以把其下的区域看成概率。

概率密度的基本含义可以用公式X-12表示：

$$f(x)dx=P[x<X<x+dx]\text{\hspace{1em}(X-12)}$$

我们前边的公式X-7可以用另外一种特别有用的形式表示：

$$P[x_1\le X\le x_2]={\int }_{x_1}{x}_{2}f(x)dx\text{\hspace{1em}(X-13)}$$

f(x)的标准形状阐述于图X-3，其中a是一个对称分布，b是一个向右倾斜的分布，c是向左倾斜的分布。（在图中，x增加相当于图形右移）。

在持续变量的情况下，概率必须用区间表示。这是因为对于指定的x值的概率一直等于0，因为在任意区间中有无数个X的值。因此$f(x)dx$是目标落在x和x+dx区间的数量的概率。当然，dx的区间长度应该尽可能的小。f(x)本身也就是单位区间的概率。在这个例子中，我们用加法符号来替代积分符号，将所有目标区间的x的概率加起来。公式X-13将适用于所有离散的X。

在先前故障案例中，$f(t)dt$给出了部件在t和t+dt之间发生故障的概率。在测量的例子中，f(x)dx给出了测量结果位于x和x+dx之间的概率。从经验角度出发，如果我们考虑大量的测量，f(x)dx可以用以下公式进行估计
$$f(x)\delta x=\frac{\delta n_i}{n}$$
这里n是测量的总次数,$\delta n_i$是X位于x和$x+\delta x$之间的数量。

5。 分布参数和矩

特定概率密度函数的特征是通过分布参数描述的。一类参数用于沿着横坐标定位分布。因此，像这类的参数被称作位置参数（location parameter)。

最常见的位置参数是统计平均数。其他常用到的位置参数有：中值（median)（50%在概率密度曲线下方的区域在中值的左边；另50%在右边）；模（mode)，位于概率曲线的最大值或“峰值”上（在二项分布或三项分布中，可能会没有最大值或有多个最大值的情况）；中列数（mid-range）,当变量在有限的区间内，它是最大值和最小值的平均值，除此之外，其他的都不很重要。图X-4展示这些概念。

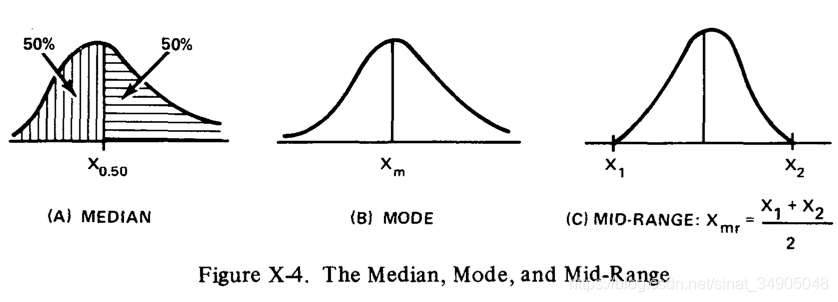
在（a)中，中值用$x_{.50}$表示。从中值的定义中可以看出，50%的次数结果将会小于等于$x_{.50}$，而50%的次数，将会大于。因此$P(x\le x_{.50})=.50$，根据累积分布，$F(x_{.50})=.50。中值是$\alpha$百分数的特殊例子，$x_\alpha$定义为F(x_{\alpha })=\alpha$，例如，90%百分数是$F(x_{.90})=.90$，90%的次数中结果中的x数值将会小于等于$x_{.90}$。

在（b）中，模是用$x_m$表示，给出了最大概率的结果的值。在©中，我们看到如何从两个极值中得出中列数。

均值（average）也被成为平均值（mean）或期望值（expected value）。如果我们重复做相同的随机实验，对结果取平均值。那么这个实际平均值会随着实验次数的增加越来越接近理论平均值。（我们假设分布存在平均值，这样实验平均值会越来越趋向于总体平均值）

在图X-3（a)中那样的对称分布的情况下，均值，中值和模是统一的。对于倾斜的分布，如图X-3（c)，中值将落于模和均值之间。在图X-5中，这两个对称分布图形有着相同的均值，中值和模。但是对于中心聚集程度的角度来看，它们却是不一样的。用来描述这分布这方面的参数叫分散参数（dispersion parameters）。其他和这个类似的参数还有方差（variance）、方差的开方和标准差（standard deviation）。其他分散参数比较少用到，是种植绝对偏差（median absolute deviation),范围在上限值和下限值之间。我们将会在后一章里边计算方差。

事实上，还有很多其他的分布参数，我们这里涉及到的都是一些基本的参数。当累积概率分布的形式确定后，我们必须掌握计算分布参数的具体方法。这些通用方法中的一些方法需要计算分布中的矩，并且在理论统计中十分重要。分布的矩可以在任意指定点上计算，但是我们限制只在（a)中计算原点的矩，(b)中计算均值的矩。

(a) 原点的矩

第一个关于原点的矩被定义如下：

$${\mu }_1^{\prime }={\int }_{-\infty }^{+\infty }xf(x)dx\text{\hspace{1em}(X-14)}$$

它表示X的平均或期望值，用$E[X]$表示。我们使用$\mu$来简单的表示均值，因为$E[X]=\mu$。

第二个关于原点的矩被定义如下：

$${\mu }_2^{\prime }={\int }_{-\infty }^{+\infty }{x}^{2}f(x)dx\text{\hspace{1em}(X-15)}$$

他表示$X^2$的期望值，$E[X^2]$。

总而言之，第n个关于原点的矩是

$${\mu }_n^{\prime }={\int }_{-\infty }^{+\infty }{x}^{n}f(x)dx\text{\hspace{1em}(X-16)}$$

表示$X^n$的期望，$E[X^n]$

如果$Y=g(X)$是任意关于X的函数，X是根据概率密度函数f(x)的分布，$g(X)$的期望可以通过如下方式获得：
$$E[Y]=E[g(X)]={\int }_{-\infty }^{+\infty }g(x)f(x)dx\text{\hspace{1em}(X-17)}$$

(b)均值的矩

第一个关于均值的矩定义如下：

$${\mu }_1={\int }_{-\infty }^{+\infty }(x-\mu )f(x)dx\text{\hspace{1em}(X-18)}$$

因为它总是等于0，所以并没有什么用处。

第二个关于均值的矩的定义如下：
$${\mu }_2={\int }_{-\infty }^{+\infty }(x-\mu {)}^{2}f(x)dx\text{\hspace{1em}(X-19)}$$

它表示了方差${\sigma }^2$或者$E[(X-\mu)^2f(x)dx]。总的来说，均值的第n个矩定义如下：

$${\mu }_n={\int }_{-\infty }^{+\infty }(x-\mu {)}^{n}f(x)dx\text{\hspace{1em}(X-20)}$$

表示$E[(X-\mu {)}^n]$。

有一个非常有用的关系：

$${\mu }_2={\mu }_2^{\prime }-({\mu }_1^{\prime }{)}^2\text{\hspace{1em}(X-21)}$$

公式21允许我们通过评估X-15中的积分，而不是X-19中更复杂的积分来计算方差。公式21可以通过如下方式得到轻易的证明：

在离散随机变量的情况下，原点的第一个矩表示为：

$$\mu ={\mu }_1^{\prime }=\sum _{i=1}^n{X}_{i}p(x_i)\text{\hspace{1em}(X-22)}$$

这里$p(x_i)$是$x_i$的概率，最常用的寻找n个值的平均值的方程如下：

$$\hat{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$

这是公式22应用的特殊情况，每个值都被认为拥有同样的出现的概率$\frac{1}{n}$。

例如，对于单一的骰子，我们有

$$\mu ={\mu }^{\prime }=\frac{1+2+3+4+5+6}{6}=3.5$$

尽管实际上不会出现这样的结果，但是期望值是3.5.

同样的，如果随机变量是离散的，那么第二个均值的矩的形式如下：

$${\mu }_2=\sum _{i=1}n(x_i-\mu {)}^{2}p(x_i)\text{\hspace{1em}(X-23)}$$

在所有$x_i$都有同样的“权重”1/n的情况下，公式X-23可以简化成计算n个读书采样的方差的采样等式：

$$s^2=\frac{1}{n}\sum _{i=1}n(x_i-\hat{x}{)}^2\text{\hspace{1em}(X-24)}$$

我们用一个应用分布矩的简单例子来总结这一节的内容。参考如图X-6那样的矩形概率密度函数，它在a和b中的任何值基本都是相等的，因为都相等，所以$f(x)=f_0$。因此，这个概率密度函数的积分应该是1，我们有：
$Area=f_0(b-a)=1$，于是$f_0=\frac{1}{b-a}$。

分布的均值（期望）计算如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cVvsse9F-1586708457771)(asserts/equationX-2.png)]

分布的方差计算如下：

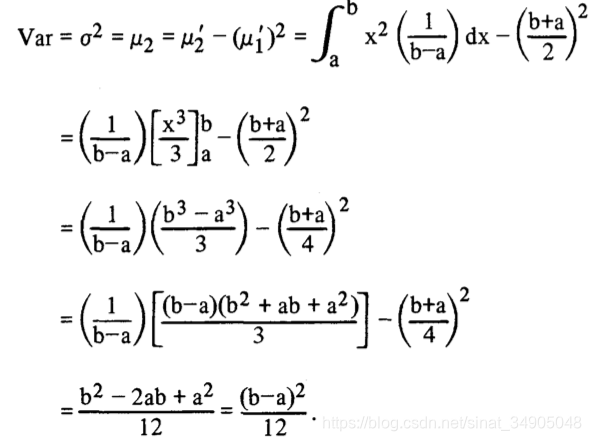
10.6 二项式的极限形式：正态分布和泊松分布

有一些很重要的分布是二项分布的极限形式。例如：
$$\underset{n\to \infty }{\lim }[C_n^x{p}^x(1-p{)}^{n-x}]$$

上面的式子是p是固定的，n趋近于无穷的一种极限形式。省略数学细节，该过程会转换成著名的正态分布形式：高斯分布。

$$f(x;\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2]\text{\hspace{1em}(X-25)}$$

这里$\mu$和$\sigma$是平均值和标准差。正态分布已经广泛的应用表格进行处理，但不是X-25那样的形式。X-25那样的表格需要对$\mu$和$\sigma$进行广泛的覆盖，这将使得表格过于臃肿而降低可用性。找到一种转换形式，将$\mu$和$\sigma$标准化，变成0和1，这是有可能的。这种转换是：

$$z=\frac{x-\mu }{\sigma }\text{\hspace{1em}(X-26)}$$

对应的基于z的表现形式为

$$f(z)=\frac{1}{\sqrt{2\pi }}{e}^{-z^2/2}\text{\hspace{1em}(X-27)}$$

这个式子被叫做标准正态分布，它是所有正态分布表格的基本形式。

读者注意到，从公式X-25经由公式X-26到公式X-27，并不是一个简单的替换的过程。这个变换用到了转换的雅克比式（参考【25】）。在这个例子中，雅克比式是$\sigma$，这里抵消了$1/(\sqrt{2\pi }\sigma )$中的$\sigma$。$f(z)$的图形如图X-7所示：

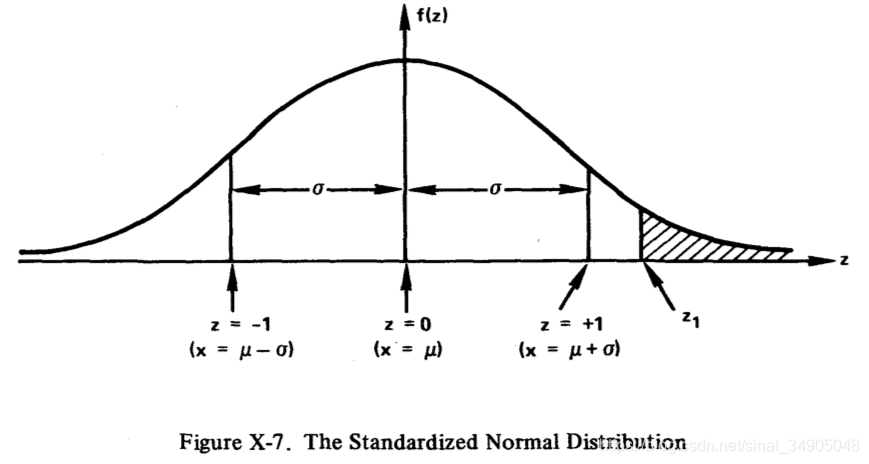
这里列举了一些标准正态分布的几个特征。其中我们最感兴趣的是曲线之下横轴上的两个点之间的部分。读者应该还记得这样的区域可以当成一个概率，因为曲线下的所有区域之和是一致的。假设存在一个点$z_1$，一些表格记录了从$z_1$到$+\infty$的曲线下的区域（图中的阴影部分）；一些表格记录了从$z_1$到$-\infty$的曲线下的区域，还有一些表格记录了从$z_1$到原点的曲线下的区域。当然，在智能的使用表格之前，必须确认要制表的区域。

对于正态分布，对于原始的变量X，$\sigma$衡量了平均值$\mu$到曲线拐点的距离，概率密度曲线从$\mu -\sigma$到$\mu +\sigma$的区域约等于0.68，从$\mu -2\sigma$到$\mu +2\sigma$约等于是0.95.

这里假设读者已经熟悉正态分布和它的表格。尽管如此，我们还是给出一个简答的数学实例，有经验的可以略过。锻件中的槽的宽度符合正态分布，它的均值$\mu$等于0.900英寸，标准差$\sigma$等于0.0030英寸。如果说明书中的限制（允许误差）为$0.9000\pm 0.0050$,占有总产出多少百分比的数将被拒绝？拒绝的锻件是其宽度数值是在图中阴影部分的那些。

对于x=0.9050的z值为
$$z=\frac{0.9050-0.9000}{0.0030}=1.67$$

从标准正态表格可以得出，右边的尾巴区域在$P[Z\ge 1.67]$等于0.0475。这是$X\ge 0.9050$的概率。由于图形是对称的，所以左边的尾巴区域也是0.0475.所以两边尾巴加在一起的就是0.0950.这就是一个零件宽度在说明书外的概率。因此，9.5%就是零件被退回的概率。

这个退回率相当高。如果说明书不做更改，我们可以通过认真工作，降低$\sigma$来降低退回率。假设我们的目标退回率是1/1000=0.001,那么最大允许的退回率$\sigma$,这里记为${\sigma }^{\prime }$，应该是多少？

如果退回率是0.001，则每个尾巴上的区域必须是0.001/2=0.0005。从表格中得出，截去0.0005区域尾巴的z的值是3.3。从$z=(x-\mu )/\sigma$我们可以得出${\sigma }^{\prime }=(x-\mu )/z$，

因此 ${\sigma }^{\prime }=\frac{0.9050-0.9000}{3.3}=0.00152英寸$。

因此，对于0.001的退回率，最大允许$\sigma$的值是0.00152英寸。

我们研究正态分布有很多种理由。其中之一就是根据中心极限定理，不管每个测量的分布如何，大量的测量的均值就趋近于正态分布。另一个理由是正态分布为许多消耗模型提供了相当好的统计模型。

从系统和可靠性分析的角度出发，另一种重要的形式是以下二项分布的极限形式：
$$\begin{gathered} n\to \infty \\ p\to 0 \end{gathered}$$