算法与数据结构新手班第5节

最新推荐文章于 2024-11-04 15:37:16 发布

一颗_豆芽菜

最新推荐文章于 2024-11-04 15:37:16 发布

阅读量89

点赞数

分类专栏：算法与数据结构文章标签：数据结构 java c++ Powered by 金山文档

本文链接：https://blog.csdn.net/beans_blog/article/details/128666669

版权

算法与数据结构专栏收录该内容

9 篇文章 0 订阅

订阅专栏

文章介绍了位图数据结构的实现，用于高效地进行数字集合的操作，如添加、删除和查找，同时展示了使用位运算实现的加法、减法、乘法和除法算法。此外，还讨论了如何合并K个升序链表的问题，利用优先队列优化合并过程。

摘要由CSDN通过智能技术生成

位图

位图的功能：能够根据需求在集合中存放数字、删除数字，并能查看集合中是否有某数字

位图的好处：占用内存少，HashSet存储相同数据占用的内存超过位图的32倍

位图的实现：

public static class BitMap {

        private long[] bits;

        public BitMap(int max) {
            //long类型上的64位的0或1状态可以表示是否有0到63这64个数
            //(max+64)>>6相当于max/64+1
            bits = new long[(max + 64) >> 6];
        }

        public void add(int num) {
            //num/64表示num在数组的第几位
            //num&63相当于num%64，即num属于数组的第几位
            bits[num >> 6] |= (1L << (num & 63));
        }

        public void delete(int num) {
            bits[num >> 6] &= ~(1L << (num & 63));
        }

        public boolean contains(int num) {
            return (bits[num >> 6] & (1L << (num & 63))) != 0;
        }
}

用位运算实现+ - * /

加法

a+b相等于a^b+(a&b)<<1，但这里还是有加号所以一直循环下去直到(a&b)<<1等于0时，可以确定0和任何数相加等于任何数

public static int add(int a, int b) {
        int sum = 0;
        while (b != 0) {
            sum = a;
            a ^= b;
            b = (sum & b) << 1;
        }
        return a;
}

减法

a-b 即 a+(-b) 因为 -b = ~b+1

public static int minus(int a,int b){
        return add(a,add(~b,1));
}

乘法

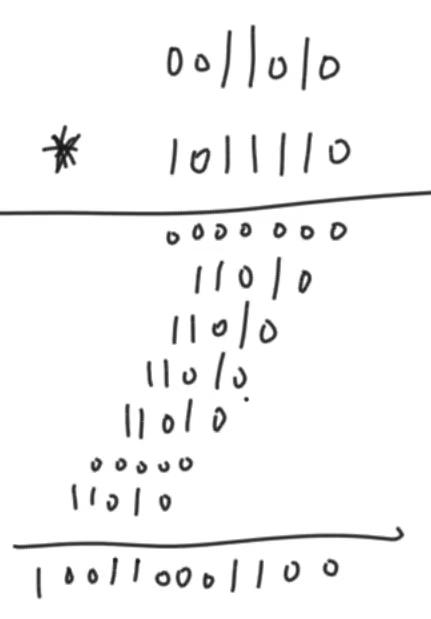
    public static int multi(int a, int b) {
        int ans = 0;
        while (b != 0) {
            if ((b & 1) != 0) {
                ans += a;
            }
            a <<= 1;
            b >>>= 1;
        }
        return ans;
    }

除法

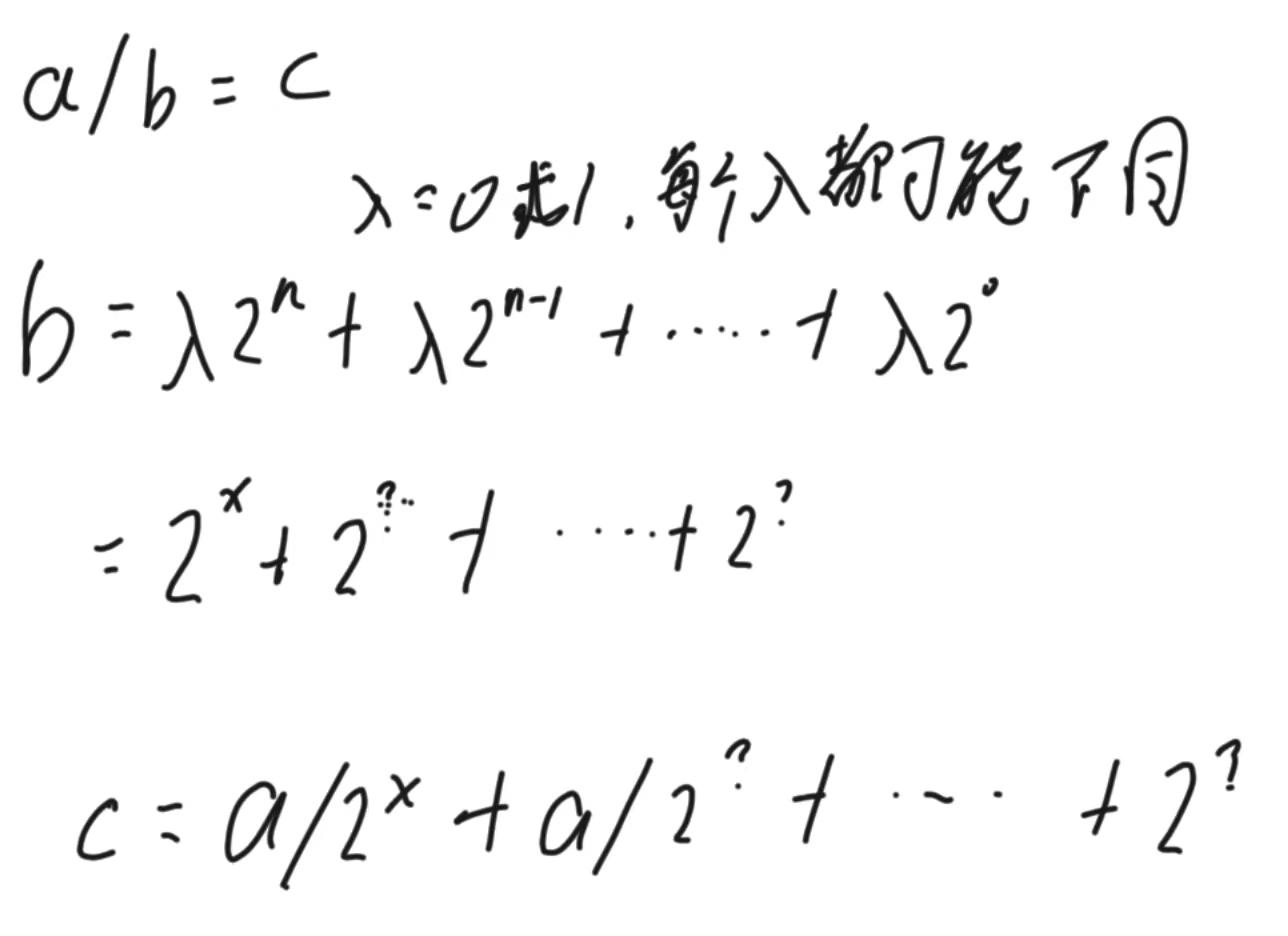
    public static int negNum(int n) {
        return add(~n, 1);
    }

    public static int div(int a, int b) {
        boolean x1 = a < 0;
        boolean y1 = b < 0;
        //将两数都弄成正数
        int x = x1 ? negNum(a) : a;
        int y = y1 ? negNum(b) : b;
        int res = 0;
        for (int i = 30; i >= 0; i = minus(i, 1)) {
            if ((x >> i) >= y) {
                res |= (1 << i);
                x = minus(x, y << i);
            }
        }
        //^相当于!=
        return x1 ^ y1 ? negNum(res) : res;
    }

    public static int divide(int a, int b) {
        //系统最小值没有对应的相反数
        if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
            return 1;
        } else if (b == Integer.MIN_VALUE) {
            return 0;
        } else if (a == Integer.MIN_VALUE) {
            if (b == negNum(1)) {
                return Integer.MAX_VALUE;
            } else {
                int c = div(add(a, 1), b);
                return add(c, div(minus(a, multi(c, b)), b));
            }
        } else {
            return div(a, b);
        }
    }

题目：合并K个升序链表

测试链接

static class ListNodeComparator implements Comparator<ListNode> {
        @Override
        public int compare(ListNode o1, ListNode o2) {
            return o1.val - o2.val;
        }

        public ListNodeComparator() {
        }
    }

    public static ListNode mergeKLists(ListNode[] lists) {
        if (lists == null) {
            return null;
        }
        PriorityQueue<ListNode> pq = new PriorityQueue<>(new ListNodeComparator());
        for (int i = 0; i < lists.length; i++) {
            if (lists[i] != null) {
                pq.add(lists[i]);
            }
        }
        if (pq.isEmpty()) {
            return null;
        }
        ListNode head = pq.poll();
        ListNode pre = head;
        if (pre.next != null) {
            pq.add(pre.next);
        }
        while (!pq.isEmpty()) {
            ListNode cur = pq.poll();
            pre.next = cur;
            pre = cur;
            if (pre.next != null) {
                pq.add(pre.next);
            }
        }
        return head;
    }