数值分析实验二

随机生成一个n阶方阵与n阶向量构成Ax=b

1、构建n阶对称正定矩阵

• 使用楚列斯基分解求x
• 使用改进的楚列斯基分解求x

代码如下：

main.m

%% A*x = b ，A为n阶对称正定矩阵，求解x
%% 使用楚列斯基分解求x
%% 使用改进的楚列斯基分解求x
 
clear all %初始化，清空变量
close all
clc %清空窗口命令
 
%% 随机生成方阵和向量
n=2;  %阶数
%生成n阶随机对称正定矩阵
M=diag(rand(n,1)); 
Z=orth(rand(n,n));
A=Z'*M*Z;    
b=rand(n,1);  %向量
 
%% 使用楚列斯基分解求x
x1 = Cholesky(A,b,n);
fprintf('******楚列斯基分解求得x=\n');
disp(x1);
 
%% 使用改进的楚列斯基分解求x
x2 = improveCholesky(A,b,n);
fprintf('******改进的楚列斯基分解求得x=\n');
disp(x2);
 
%% 求矩阵A的条件数 
cond1 = cond(A,1);  %1-范数
cond2 = cond(A,2);  %2-范数
cond3 = cond(A,inf);  %∞-范数
fprintf('******矩阵A的条件数为：%d, %d, %d\n',cond1,cond2,cond3);

Cholesky.m

function x = Cholesky(A,b,n)
%楚列斯基法求解线性方程组 A*x = b
lambda = eig(A);   %用eig求矩阵A的特征值
L = chol(A);  %用matlab内置函数chol将正定对称矩阵分解为上三角和下三角，即A=L*L'，函数返回上三角
%% 解L'y = b,L'是对应的下三角矩阵
y(1) = b(1)/L(1,1);
if n>1
    for i=2:n
        y(i) = (b(i)-L(1:i-1,i)'*y(1:i-1)')/L(i,i);
    end
end
%% 解Lx = y
x(n) = y(n)/L(n,n);
if n>1
    for i=n-1:-1:1
        x(i) = (y(i)-L(i,i+1:n)*x(i+1:n)')/L(i,i);
    end
end
x = x';
end

improveCholesky.m

function x = improveCholesky(A,b,n)
%改进楚列斯基法求解线性方程组 A*x = b
L = zeros(n,n);
D = diag(n,0);  %主对角矩阵
S = L*D;
for i = 1:n
    L(i,i) = 1;
end
%% 由A=LDL'分解得到L和D
D(1,1)=A(1,1);
for i=2:n
    for j=1:i-1
        S(i,j)=A(i,j)-sum(S(i,1:j-1)*L(j,1:j-1)');
        L(i,1:i-1)=S(i,1:i-1)/D(1:i-1,1:i-1);
    end
    D(i,i) = A(i,i)-sum(S(i,1:i-1)*L(i,1:i-1)');
end
y = zeros(n,1);
x = zeros(n,1);
%% 由LDy=b求解y
for i = 1:n
    y(i) = (b(i)-sum(L(i,1:i-1)*D(1:i-1,1:i-1)*y(1:i-1)))/D(i,i);
end
%% 由L'x=y求解y
for i = n:-1:1
    x(i) = y(i)-sum(L(i+1:n,i)'*x(i+1:n));
end

结果如图：

2、构建n阶对角占优不可约的三对角矩阵

• 使用简化计算的LU分解求x

代码如下：

%% A*x = b ，A为n阶对称正定矩阵，求解x
 
clear all %初始化，清空变量
close all
clc %清空窗口命令
 
%% 生成方阵和向量
n=4;  %阶数
%n阶对角占优不可约的三对角矩阵
A=[2,2,0,0;
   1,3,-1,0;
   0,1,6,3;
   0,0,2,5];
 
d = rand(n,1);  %向量
 
%% 使用简化计算的LU分解求x
if ~isequal(tril(A,-1)-diag(diag(tril(A,-1),-1),-1),zeros(size(A)))
error('输入矩阵不是一个三角矩阵');
end
if ~isequal(triu(A,1)-diag(diag(triu(A,1),1),1),zeros(size(A)))
error('输入矩阵不是一个三角矩阵');
end
a=[0;diag(tril(A,-1),-1)];%下对角线
b=diag(A);%中对角线
c=[diag(triu(A,1),1);0];%上对角线
l=zeros(size(a,1),1);%求L
u=zeros(size(b,1),1);%求U
n=size(b,1);%矩阵的维度
x=zeros(n,1);
y=zeros(n,1);
u(1)=b(1);
for i=2:n
    l(i)=a(i)/u(i-1);
    u(i)=b(i)-l(i)*c(i-1);
end
y(1)=d(1);
for i=2:n
    y(i)=d(i)-l(i)*y(i-1);
end
x(n)=y(n)/u(n);
for i=n-1:-1:1
    x(i)=(y(i)-c(i)*x(i+1))/u(i);
end
 
fprintf('******追赶法求得x=\n');
disp(x);
%% 求矩阵A的条件数 
cond1 = cond(A,1);  %1-范数
cond2 = cond(A,2);  %2-范数
cond3 = cond(A,inf);  %∞-范数
fprintf('******矩阵A的条件数为：%d, %d, %d\n',cond1,cond2,cond3);

结果如图：

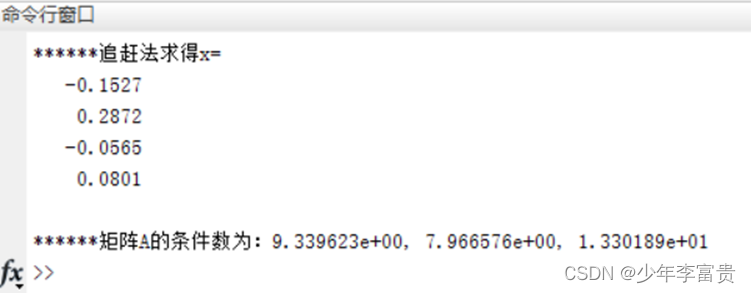
3、求以上矩阵的条件数

• 包括1-范数、2-范数和∞-范数的条件数

答：包含在上述代码中。