决策树算法:顾名思义,以二分类问题为例,即利用自变量构造一颗二叉树,将目标变量区分出来,所有决策树算法的关键点如下:
1.分裂属性的选择。即选择哪个自变量作为树叉,也就是在n个自变量中,优先选择哪个自变量进行分叉。而采用何种计算方式选择树叉,决定了决策树算法的类型,即ID3、c4.5、CART三种决策树算法选择树叉的方式是不一样的,后文详细描述。
2.树剪枝。即在构建树叉时,由于数据中的噪声和离群点,许多分支反映的是训练数据中的异常,而树剪枝则是处理这种过分拟合的数据问题,常用的剪枝方法为先剪枝和后剪枝。后文详细描述。
为了描述方便,本文采用评价电信服务保障中的满意度预警专题来解释决策树算法,即假如我家办了电信的宽带,有一天宽带不能上网了,于是我打电话给电信报修,然后电信派相关人员进行维修,修好以后电信的回访专员询问我对这次修理障碍的过程是否满意,我会给我对这次修理障碍给出相应评价,满意或者不满意。根据历史数据可以建立满意度预警模型,建模的目的就是为了预测哪些用户会给出不满意的评价。目标变量为二分类变量:满意(记为0)和不满意(记为1)。自变量为根据修理障碍过程产生的数据,如障碍类型、障碍原因、修障总时长、最近一个月发生故障的次数、最近一个月不满意次数等等。简单的数据如下:
客户ID 故障原因 故障类型 修障时长 满意度
001 1 5 10.2 1
002 1 5 12 0
003 1 5 14 1
004 2 5 16 0
005 2 5 18 1
006 2 6 20 0
007 3 6 22 1
008 3 6 23 0
009 3 6 24 1
010 3 6 25 0
故障原因和故障类型都为离散型变量,数字代表原因ID和类型ID。修障时长为连续型变量,单位为小时。满意度中1为不满意、0为满意。
下面沿着分裂属性的选择和树剪枝两条主线,去描述三种决策树算法构造满意度预警模型:
分裂属性的选择:即该选择故障原因、故障类型、修障时长三个变量中的哪个作为决策树的第一个分支。
ID3算法是采用信息增益来选择树叉,c4.5算法采用增益率,CART算法采用Gini指标。此外离散型变量和连续型变量在计算信息增益、增益率、Gini指标时会有些区别。详细描述如下:
1.ID3算法的信息增益:
信息增益的思想来源于信息论的香农定理,ID3算法选择具有最高信息增益的自变量作为当前的树叉(树的分支),以满意度预警模型为例,模型有三个自变量:故障原因、故障类型、修障时长。分别计算三个自变量的信息增益,选取其中最大的信息增益作为树叉。信息增益=原信息需求-要按某个自变量划分所需要的信息。
如以自变量故障原因举例,故障原因的信息增益=原信息需求(即仅仅基于满意度类别比例的信息需求,记为a)-按照故障原因划分所需要的信息需求(记为a1)。
其中原信息需求a的计算方式为:
其中D为目标变量,此例中为满意度。m=2,即满意和不满意两种情况。Pi为满意度中属于分别属于满意和不满意的概率。此例中共计10条数据,满意5条,不满意5条。概率都为1/2。Info(满意度)即为仅仅基于满意和满意的类别比例进行划分所需要的信息需求,计算方式为:
按照故障原因划分所需要的信息需求(记为a1)可以表示为:
其中A表示目标变量D(即满意度)中按自变量A划分所需要的信息,即按故障类型进行划分所需要的信息。V表示在目标变量D(即满意度)中,按照自变量A(此处为故障原因)进行划分,即故障原因分别为1、2、3进行划分,将目标变量分别划分为3个子集,{D1、D2、D3},因此V=3。即故障原因为1的划分中,有2个不满意和1个满意。D1即指2个不满意和1个满意。故障原因为2的划分中,有1个不满意和2个满意。D2即指1个不满意和2个满意。故障原因为3的划分中,有2个不满意和2个满意。D3即指2个不满意和2个满意。具体公式如下:
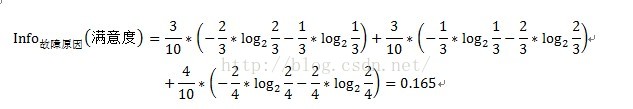
注:此处的计算结果即0.165不准确,没有真正去算,结果仅供参考。
因此变量故障原因的信息增益Gain(故障原因)=Info(满意度)- Info故障原因(满意度)=1-0.165=0.835
同样的道理,变量故障类型的信息增益计算方式如下:
变量故障类型的信息增益Gain(故障类型)=1-0.205=0.795
故障原因和故障类型两个变量都是离散型变量,按上述方式即可求得信息增益,但修障时长为连续型变量,对于连续型变量该怎样计算信息增益呢?只需将连续型变量由小到大递增排序,取相邻两个值的中点作为分裂点,然后按照离散型变量计算信息增益的方法计算信息增益,取其中最大的信息增益作为最终的分裂点。如求修障时长的信息增益,首先将修障时长递增排序,即10.2、12、14、16、18、20、22、23、24、25,取相邻两个值的中点,如10.2和12,中点即为(10.2+12)/2=11.1,同理可得其他中点,分别为11.1、13、15、17、19、21、22.5、23.5、24.5。对每个中点都离散化成两个子集,如中点11.1,可以离散化为两个<=11.1和>11.1两个子集,然后按照离散型变量的信息增益计算方式计算其信息增益,如中点11.1的信息增益计算过程如下:
中点13的信息增益计算过程如下:
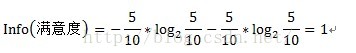
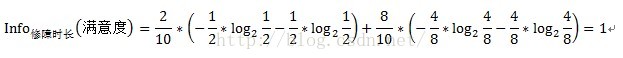
中点11.1的信息增益Gain(修障时长)=1-1=0
同理分别求得各个中点的信息增益,选取其中最大的信息增益作为分裂点,如取中点11.1。然后与故障原因和故障类型的信息增益相比较,取最大的信息增益作为第一个树叉的分支,此例中选取了故障原因作为第一个分叉。按照同样的方式继续构造树的分支。
总之,信息增益的直观解释为选取按某个自变量划分所需要的期望信息,该期望信息越小,划分的纯度越高。因为对于某个分类问题而言,Info(D)都是固定的,而信息增益Gain(A)=Info(D)-InfoA(D) 影响信息增益的关键因素为:-InfoA(D),即按自变量A进行划分,所需要的期望信息越小,整体的信息增益越大,越能将分类变量区分出来。
2.C4.5算法的增益率:
由于信息增益选择分裂属性的方式会倾向于选择具有大量值的属性(即自变量),如对于客户ID,每个客户ID对应一个满意度,即按此变量划分每个划分都是纯的(即完全的划分,只有属于一个类别),客户ID的信息增益为最大值1。但这种按该自变量的每个值进行分类的方式是没有任何意义的。为了克服这一弊端,有人提出了采用增益率(GainRate)来选择分裂属性。计算方式如下:
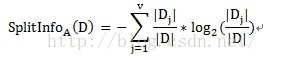
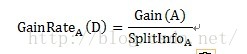
其中Gain(A)的计算方式与ID3算法中的信息增益计算方式相同。
以故障原因为例:
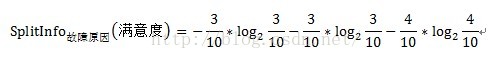
=1.201
Gain(故障原因)=0.835(前文已求得)
GainRate故障原因(满意度)=1.201/0.835=1.438
同理可以求得其他自变量的增益率。
选取最大的信息增益率作为分裂属性。
3.CART算法的Gini指标:
CART算法选择分裂属性的方式是比较有意思的,首先计算不纯度,然后利用不纯度计算Gini指标。以满意度预警模型为例,计算自变量故障原因的Gini指标时,先按照故障原因可能的子集进行划分,即可以将故障原因具体划分为如下的子集:{1,2,3}、{1,2}、{1,3}、{2,3}、{1}、{2}、{3}、{},共计8(2^V)个子集。由于{1,2,3}和{}对于分类来说没有任何意义,因此实际分为2^V-2共计6个有效子集。然后计算这6个有效子集的不纯度和Gini指标,选取最小的Gini指标作为分裂属性。
不纯度的计算方式为:
pi表示按某个变量划分中,目标变量不同类别的概率。
某个自变量的Gini指标的计算方式如下:
对应到满意度模型中,A为自变量,即故障原因、故障类型、修障时长。D代表满意度,D1和D2分别为按变量A的子集所划分出的两个不同元组,如按子集{1,2}划分,D1即为故障原因属于{1,2}的满意度评价,共有6条数据,D2即故障原因不属于{1,2}的满意度评价,共有3条数据。计算子集{1,2}的不纯度时,即Gini(D1),在故障原因属于{1,2}的样本数据中,分别有3条不满意和3条满意的数据,因此不纯度为1-(3/6)^2-(3/6)^2=0.5。
以故障原因为例,计算过程如下:
计算子集故障原因={1,3}的子集的Gini指标时,D1和D2分别为故障原因={1,3}的元组共计7条数据,故障原因不属于{1,3}的元组即故障原因为2的数据,共计3条数据。详细计算过程如下:
=0.52
树的剪枝:
树剪枝可以分为先剪枝和后剪枝。
先剪枝:通过提前停止树的构造,如通过决定在给定的节点不再分裂或划分训练元组的子集,而对树剪枝,一旦停止,该节点即成为树叶。在构造树时,可以使用诸如统计显著性、信息增益等度量评估分裂的优劣,如果划分一个节点的元组低于预先定义阈值的分裂,则给定子集的进一步划分将停止。但选取一个适当的阈值是困难的,较高的阈值可能导致过分简化的树,而较低的阈值可能使得树的简化太少。
后剪枝:它由完全生长的树剪去子树,通过删除节点的分支,并用树叶替换它而剪掉给定节点的子树,树叶用被替换的子树中最频繁的类标记。
其中c4.5使用悲观剪枝方法,CART则为代价复杂度剪枝算法(后剪枝)。
对比总结:
一、 C&R 树
classification and regression trees 是一种基于树的分类和预测方法,模型使用简单,易于理解(规则解释起来更简明易),该方法通过在每个步骤最大限度降低不纯洁度,使用递归分区来将训练记录分割为组。然后,可根据使用的建模方法在每个分割处自动选择最合适的预测变量。如果节点中100% 的观测值都属于目标字段的一个特定类别,则该节点将被认定为“纯洁”。目标和预测变量字段可以是范围字段,也可以是分类字段;所有分割均为二元分割(即分割为两组)。分割标准用的是基尼系数(Gini Index)。
CART即分类回归树。如果目标变量是离散变量,则是classfication Tree,如果目标是连续变量,则是Regression Tree。
CART树是二叉树。 二叉树有什么优点?不像多叉树那样形成过多的数据碎片
二、C4.5离散化的过程
择的目标分类有关不确定性的最佳评估方法是平均信息量,即信息嫡(Entropy):
优点:执行效率和内存使用改进、适用大数据集
CART与ID3的区别
通过之前的研究发现,CART与ID3算法都是基于信息论的决策树算法,CART算法是一种通过计算Diversity(整体)-diversity(左节点)-diversity(右节点)的值取最佳分割的算法。ID3和CART算法的区别主要集中在树的生成和树的修剪方面,但是ID3算法只能处理离散型的描述性属性。C4.5算法是ID3算法的后续算法,它能够处理连续型数据。
CART中用于选择变量的不纯性度量是Gini指数;
如果目标变量是标称的,并且是具有两个以上的类别,则CART可能考虑将目标类别合并成两个超类别(双化);
三、
优点:运算过程比C&R 树更简单有效quick unbiased efficient statistical tree (快速无偏有效的统计树)QUEST 节点可提供用于构建决策树的二元分类法,此方法的设计目的是减少大型 C&R 决策树分析所需的处理时间,同时减小分类树方法中常见的偏向类别较多预测变量的趋势。预测变量字段可以是数字范围的,但目标字段必须是分类的。所有分割都是二元的。
四、CHAID决策树
优点(chi-squared automatic interaction detection,卡方自动交互检测),通过使用卡方统计量识别最优分割来构建决策树的分类方法
2)
3)
4)
五、树的剪枝理论
1.树的生长及变量处理
(1)对于离散变量X(x1…xn),分别取X变量各值的不同组合,将其分到树的左枝或右枝,并对不同组合而产生的树,进行评判,找出最佳组合。如变量年纪,其值有“少年”、“中年”、“老年”,则分别生产{少年,中年}和{老年},{上年、老年}和{中年},{中年,老年}和{少年},这三种组合,最后评判对目标区分最佳的组合。
(2)对于连续变量X(x1…xn),首先将值排序,分别取其两相邻值的平均值点作为分隔点,将树一分成左枝和右枝,不断扫描,进而判断最佳分割点。
2. 变量和最佳切分点选择原则
树的生长,总的原则是,让枝比树更纯,而度量原则是根据不纯对指标来衡量,对于分类树,则用GINI指标、Twoing指标、Order Twoing等;如果是回归树则用,最小平方残差、最小绝对残差等指标衡量
(1)GINI指标(Gini越小,数据越纯)——针对离散目标
(2)最小平方残差——针对连续目标
其思想是,让组内方差最小,对应组间方差最大,这样两组,也即树分裂的左枝和右枝差异化最大。
(3)通过以上不纯度指标,分别计算每个变量的各种切分/组合情况,找出该变量的最佳值组合/切分点;再比较各个变量的最佳值组合/切分点,最终找出最佳变量和该变量的最佳值组合/切分点
3. 目标值的估计
(1)分类树:最终叶子中概率最大的类
(2)回归树:最终叶子的均值或者中位数
4.树的剪枝
(1)前剪枝( Pre-Pruning)
通过提前停止树的构造来对决策树进行剪枝,一旦停止该节点下树的继续构造,该节点就成了叶节点。一般树的前剪枝原则有:
a.节点达到完全纯度
b.树的深度达到用户所要的深度
c.节点中样本个数少于用户指定个数
d.不纯度指标下降的最大幅度小于用户指定的幅度
(2)后剪枝( Post-Pruning)
首先构造完整的决策树,允许决策树过度拟合训练数据,然后对那些置信度不够的结点的子树用叶结点来替代。CART 采用Cost-Complexity Pruning(代价-复杂度剪枝法),代价(cost) :主要指样本错分率;复杂度(complexity) :主要指树t的叶节点数,(Breiman…)定义树t的代价复杂度(cost-complexity):
注:参数α:用于衡量代价与复杂度之间关系,表示剪枝后树的复杂度降低程度与代价间的关系,如何定义α?
对t来说,剪掉它的子树s,以t中最优叶节点代替,得到新树new_t。 new_t可能会比t对于训练数据分错M个,但是new_t包含的叶节点数,却比t少:
5.CCP剪枝步骤:
第一步:
–
–
–
第二步:
–
–
–
参考文献:
http://blog.sina.com.cn/s/blog_7399ad1f01014wec.html
http://blog.sina.com.cn/s/blog_4e4dec6c0101fdz6.html
http://blog.sina.com.cn/s/blog_5d6632e70101gh79.html









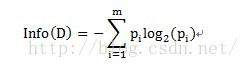
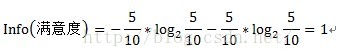
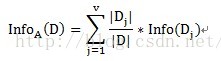
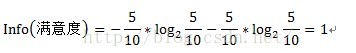
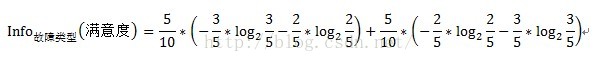
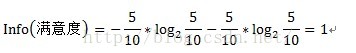
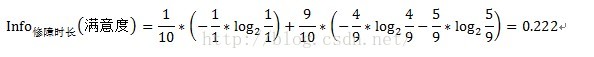
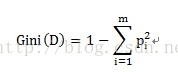
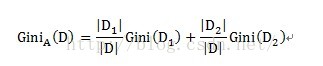
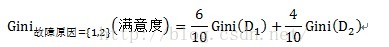
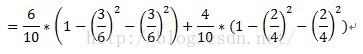
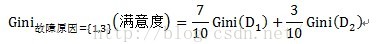
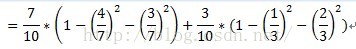





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








