并查集是一种简单的用途广泛的集合. 并查集是若干个不相交集合,能够实现较快的合并和判断元素所在集合的操作,应用很多,如其求无向图的连通分量个数等。最完美的应用当属:实现Kruskar算法求最小生成树
并查集的精髓(即它的三种操作,结合实现代码模板进行理解):
1、Make_Set(x)把每一个元素初始化为一个集合
初始化后每一个元素的父亲节点是它本身,每一个元素的祖先节点也是它本身(也可以根据情况而变)。
2、Find_Set(x)查找一个元素所在的集合
查找一个元素所在的集合,其精髓是找到这个元素所在集合的祖先!这个才是并查集判断和合并的最终依据。
判断两个元素是否属于同一集合,只要看他们所在集合的祖先是否相同即可。
合并两个集合,也是使一个集合的祖先成为另一个集合的祖先,具体见示意图
3、Union(x,y)合并x,y所在的两个集合
合并两个不相交集合操作很简单:
利用Find_Set找到其中两个集合的祖先,将一个集合的祖先指向另一个集合的祖先。如图
l 并查集的优化
1、Find_Set(x)时 路径压缩
寻找祖先时我们一般采用递归查找,但是当元素很多亦或是整棵树变为一条链时,每次Find_Set(x)都是O(n)的复杂度,有没有办法减小这个复杂度呢?
答案是肯定的,这就是路径压缩,即当我们经过"递推"找到祖先节点后,"回溯"的时候顺便将它的子孙节点都直接指向祖先,这样以后再次Find_Set(x)时复杂度就变成O(1)了,如下图所示;可见,路径压缩方便了以后的查找。
2、Union(x,y)时 按秩合并
即合并的时候将元素少的集合合并到元素多的集合中,这样合并之后树的高度会相对较小。
poj2524
#include<stdio.h>
#include<stdlib.h>
int father[50005];
void Make_set(int x)
{
father[x]=x;
}
int Find_set(int x)
{
if(father[x]==x)
return x;
father[x]=Find_set(father[x]);
return father[x];
}
void Union_set(int x,int y)
{
int rx=Find_set(x);
int ry=Find_set(y);
if(rx!=ry)
{
father[ry]=rx;
}
}
int main()
{
int n,m,i,j,num,sum=0,x,y,rx,ry;
while(scanf("%d%d",&n,&m))
{
if(n==0&&m==0)
break;
num=n;
sum=sum+1;
for(i=1;i<=n;i++)
{
Make_set(i);
}
for(i=0;i<m;i++)
{
scanf("%d%d",&x,&y);
rx=Find_set(x);
ry=Find_set(y);
if(rx!=ry)
{
num=num-1;
Union_set(x,y);
}
}
printf("Case %d: %d\n",sum,num);
}
system("pause");
return 0;
}
poj1611
The Suspects
| Time Limit: 1000MS |
| Memory Limit: 20000K |
| Total Submissions: 8313 |
| Accepted: 3920 |
Description
Severe acuterespiratory syndrome (SARS), an atypical pneumonia of unknown aetiology, wasrecognized as a global threat in mid-March 2003. To minimize transmission toothers, the best strategy is to separate the suspects from others.
In the Not-Spreading-Your-Sickness University (NSYSU), there are many studentgroups. Students in the same group intercommunicate with each other frequently,and a student may join several groups. To prevent the possible transmissions ofSARS, the NSYSU collects the member lists of all student groups, and makes thefollowing rule in their standard operation procedure (SOP).
Once a member in a group is a suspect, all members in the group are suspects.
However, they find that it is not easy to identify all the suspects when astudent is recognized as a suspect. Your job is to write a program which findsall the suspects.
Input
The input filecontains several cases. Each test case begins with two integers n and m in aline, where n is the number of students, and m is the number of groups. You mayassume that 0 < n <= 30000 and 0 <= m <= 500. Every student isnumbered by a unique integer between 0 and n−1, and initially student 0 isrecognized as a suspect in all the cases. This line is followed by m memberlists of the groups, one line per group. Each line begins with an integer k byitself representing the number of members in the group. Following the number ofmembers, there are k integers representing the students in this group. All theintegers in a line are separated by at least one space.
A case with n = 0 and m = 0 indicates the end of the input, and need not beprocessed.
Output
For each case, outputthe number of suspects in one line.
Sample Input
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0
Sample Output
4
1
1
翻译:SARS,非典型肺炎,未知的病因,被认为是03年对全球的一个威胁,为了防止SARS在人群之中传染,最好的办法是将可能患病的人隔离起来。
在NSYSU大学,这里有许多学生团队。在同一个团队里面的学生频繁地相互交流,而且一个学生可能加入了多个团队。为了阻止SARS传播的可能,NSYSU收集了学生团队的信息,并且制定了下面的规则在他们的标准操作程序里面。
一旦在一个组(即团队)里面有一个感染嫌疑者,则这个组都是感染嫌疑者。
然而,他们发现要坚定所有嫌疑者并不容易,当一个学生被认为是感染嫌疑者的时候。你的工作就是写一个程序来找出所有的感染嫌疑者。
输出包括了一些情况。每一个情况以两个整数开始作为一行,n代表学生的数目,m代表组的数目。你可以假设0<n<=30000,而且0<=m<=500。每一个学生从0到n-1标号,并且最初认为0号学生是感染嫌疑者在每一个情况里面。后面的m行,每行表示一个组。每一行开始的数k为这个组的学生人数,然后是这个组里面的k个学生编号,所有的学生编号在同一行的以至少一个空格隔开。
对于情况n=0且m=0的表示输入结束,不进行任何操作。
解题思路:使用并查集,每输入一行学生编号数据后,都判断第一个学生编号的祖先是否和后面每一个学生编号的祖先相同,若不同,则将第一个编号的祖先变为该后面编号的祖先,将集合合并,且每合并一次,第一个编号的祖先上的元素个数都等于合并之前两个祖先上的元素个数之和(最初,每一个编号的祖先都是该编号自身,且对应的元素个数都为一),最后输出编号为0的祖先上的元素个数即可
总结及出错情况:该题主要就是使用并查集,注意在合并的时候祖先上的元素个数要更新,且最初的时候每一个编号的祖先上的元素个数都是一,最易出错的就是在输入的数据中没有0就以为没有感染嫌疑者,其实这种情况应该是有一个,因为0在每一种情况中都是有的,且0编号代表的学生就是感染嫌疑者
代码:#include<iostream>
using namespace std;
int father[30005],num[30005];
void Make(int x)
{
father[x]=x;
num[x]=1;
}
int Find(int x)
{
if(father[x]==x)
return x;
father[x]=Find(father[x]);
return father[x];
}
void Union(int x,int y)
{
int rx=Find(x);
int ry=Find(y);
if(rx!=ry)
{
father[ry]=rx;
num[rx]=num[rx]+num[ry];
}
}
int main()
{
int n,m,i,j;
while(cin>>n>>m)
{
if(n==0&&m==0)
break;
for(i=0;i<n;i++)
{
Make(i);
}
for(i=0;i<m;i++)
{
int k,first,b;
cin>>k>>first;
for(j=1;j<k;j++)
{
cin>>b;
Union(first,b);
}
}
cout<<num[Find(0)]<<endl;
}
system("pause");
return 0;
}
poj1182
http://blog.csdn.net/balloons2012/article/details/7871104
http://blog.csdn.net/yihuikang/article/details/7865923
http://blog.csdn.net/c0de4fun/article/details/7318642
#include<stdio.h>
#include<stdlib.h>
int father[50005];
int rank[50005];
int Find(int x)
{
int t;
if(father[x]==x)
return x;
t=father[x];
father[x]=Find(father[x]);
rank[x]=(rank[t]+rank[x])%3;
return father[x];
}
void Union(int a,int b,int c)
{
int ra=Find(a);
int rb=Find(b);
father[ra]=rb;
rank[ra]=(rank[b]-rank[a]+3+c)%3;
}
int main()
{
int i,n,k;
int d,x,y;
int rx,ry;
int sum=0;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)
{
father[i]=i;
}
while(k--)
{
scanf("%d%d%d",&d,&x,&y);
if(x>n||y>n||(d==2&&x==y))
{
sum=sum+1;
}
else
{
rx=Find(x);
ry=Find(y);
if(rx==ry)
{
if((rank[x]-rank[y]+3)%3!=d-1)
sum=sum+1;
}
else
Union(x,y,d-1);
}
}
printf("%d\n",sum);
system("pause");
return 0;
}
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
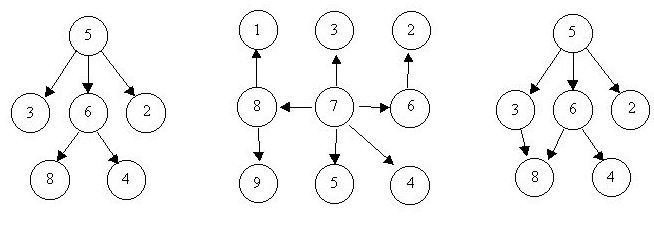
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Sample Input
6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1
Sample Output
Case 1 is a tree. Case 2 is a tree. Case 3 is not a tree.
/* POJ 1308
* By Ceeji
* http://poj.org/problem?id=1308
*
*/
#include <iostream>
#include <cstring>
using namespace std;
const int MAX_N = 200;
int father[MAX_N];
bool has_point[MAX_N];
int case_number = 0;
void init_set ()
{
memset (father, 0, sizeof(father)); // 0 means that the father is itself.
memset (has_point, 0, sizeof(has_point));
}
int get_father (const int i)
{
if (father[i] == 0 || father[i] == i)
{
father[i] = i;
return i;
}
int tmp = get_father(father[i]);
father[i] = tmp;
return tmp;
}
/* union : point x to y */
void set_union (const int x, const int y)
{
int fx = get_father(x);
int fy = get_father(y);
father[fx] = fy;
}
int maxof (const int x, const int y)
{
return x > y ? x : y;
}
int do_work ()
{
init_set ();
int s, t, max = 0;
bool finish = false;
while (cin >> s >> t)
{
if (s > 0 && t > 0) // if s or t is not greater than 0, it is the end descripter.
{
max = maxof (maxof (max, s), t);
has_point[s] = true;
has_point[t] = true;
if (get_father(s) != get_father(t))
set_union(s, t);
else
{
cout << "Case " << case_number << " is not a tree." << endl;
finish = true;
}
}
else
{
if (s == -1 && t == -1)
{
return 1;
}
break;
}
}
if (!finish)
{
int f = get_father(max);
for (int i = 2; i <= max; ++i)
if (has_point[i] && get_father(i) != f)
{
cout << "Case " << case_number << " is not a tree." << endl;
finish = true;
break;
}
}
if (!finish)
cout << "Case " << case_number << " is a tree." << endl;
return 0;
}
int main()
{
while (true)
{
++case_number;
if (do_work())
return 0;
}
return 0;
}
poj 1984
http://blog.csdn.net/waitfor_/article/details/7828791
























 2205
2205

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








