稀疏矩阵(Sparse Matrix)由于有很多0,为了节省空间,一般压缩存储。通常只需要保存非零元素及其位置即可。
下面介绍Compressed Row Storage(CRS)格式或者称为 Compressed sparse row(CSR)格式,由名称可见,该格式是把行的信息压缩存储了,只显式保留每行第一个非零元素的位置,具体在例子中可以看到。
假设有稀疏矩阵A,我们需要创建三个数组,一个浮点型数组val,另外两个为整型数组(col_ind, row_ptr)。
val数组,大小为矩阵A的非零元素的个数,保存矩阵A的非零元素(按从上往下,从左往右的行遍历方式访问元素)。
col_ind数组,和val数组一样,大小为矩阵A的非零元素的个数,保存val数组中元素的列索引。其数学表示为:
row_ptr数组,大小为矩阵A的行数,保存矩阵A的每行第一个非零元素在val中的索引。其数学表示为:
按照惯例,一般定义row_ptr(n+1) = nnz + 1,而nnz是A中非零元素的个数。
该方法可以节省很多空间,只需要2nnz + n + 1个存储单元,而不是n的平方个单元。
看一个例子:
矩阵A定义为
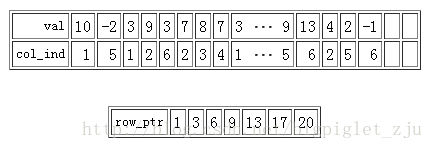
其CSR格式由三个数组定义为:
注意其中row_ptr数组的最后一个元素为20(19+1),因为矩阵A的非零元素为19。
参考:
1, Compressed Row Storage
http://web.eecs.utk.edu/~dongarra/etemplates/node373.html
2, Sparse Matrix Compression Formats
http://www.cs.colostate.edu/~mroberts/toolbox/c++/sparseMatrix/sparse_matrix_compression.html


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








