深度学习-2.机器学习基础

机器学习问题举例

• 分类问题
• 输入确实的分类问题
• 回归问题
• 转录问题
  • 机器学习系统观察到一系列非结构化的数据，并转录成离散的文本形式。
  • 如将街道门牌图片转化成数字、语音识别等
• 机器翻译
• 结构化输出
  • 将数据输出成向量或其他数据结构，这些结构之间还拥有重要的关系
  • 将图片转换成文字描述，标注航拍照片中的道路位置等
• 异常检测
  • 样本数量及其不均衡的分类问题，且在样本分布上也拥有分类问题所没有的分布特征
• 合成与采样
  • 通过已有的样本生成新样本
• …

性能度量P

TP: True Positive,将正类预测类正类的样本数量
FN: False Negtive,将正类预测为负类的样本数量
FP: False Positive,将负类预测为正类的样本数量
TN: True Negtive,将负类预测为负类的样本数量

• 准确率ACC
  $$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$
• 精确度precision
  $$p=\frac{TP}{TP+FP}$$
• 召回率
  $$r=\frac{TP}{TP+FN}$$

其他指标将在后续文章中

容量、过拟合和欠拟合

定义

• 泛化：在先前没有预测到的数据输入上表现良好的能力

• 训练误差
  $$trainningerror=\frac{||X^{(train)}\omega -y^{(train)}|{|}_2^2}{m^{train}}$$

• 测试误差
  $$testerror=\frac{||X^{(test)}\omega -y^{(test)}|{|}_2^2}{m^{test}}$$

• 容量：模型拟合各种函数的能力。

• 过拟合：训练误差和测试误差之间的差距较大

• 欠拟合：由于训练次数不足导致的训练误差较大
  

• 假设空间：学习算法可以选择为解决方案的函数集，是一种控制训练算法容量的方法。

性质

• 通过调整容量，可以防止出现过拟合和欠拟合。
• 通过改变输入特征的数量和加入特征对应的参数可以改变模型的容量。
• 模型的选择也会影响模型的容量，这部分被影响的容量被称为表示容量，通常情况下，从函数族中挑选出一个最优函数来拟合样本分布是很难的一件事，因此实际上的学习算法不会真的找到最优函数，而是找到一个可以大大降低训练误差的函数。
• 如果优化算法不完美，则该学习算法的有效容量将小于模型族的表示容量

相关理论

奥卡姆剃刀原理

• 内容：在同样能够解释已知观测现象的假设中，我们应该挑选最简单的那一个
• 性质：简单的函数能够降低过拟合的风险，使模型更加泛化，但需求的模型容量上升时，增大模型函数的复杂度也是必不可少的。
• 泛化误差曲线
  
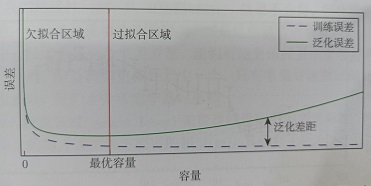
  当容量超过最优容量时模型过拟合，反之模型欠拟合

没有免费的午餐定理

• 内容：在所有可能的数据分布上平均之后，每一个分类算法在未事先观测的点上都有相同的错误率。
• 意义：该定理告诉我们必须在特定的任务上选择特定的算法。

监督学习算法

概率监督学习——逻辑回归（Logistic Regression）

基本思想

通过定义一族不同的概率分布，可以将线性回归推广到分类情况中。
如果有两个类0和1，则类1的概率决定了类0的概率，因为$P(Y=1)=1-P(Y=0)$。同时线性回归的分布是用均值参数化的而二元变量的分布必须是在0到1之间。解决这个问题的办法是使用logistic sigmoid函数，即$$\frac{1}{1+e^{-(x-\mu )/y}}$$

详解

1.预测函数

对于一个二分类问题，假设决策边界是$\omega x+b=0$，对任意一个$x\in dataSet$，预测函数为$$y=\frac{1}{1+e^{-(\omega \top x+b)}}，y\in [0,1]$$
经过简化得到
$$ln\frac{y}{1-y}=\omega \top x+b$$
令y表示x被分为1类，则1-y表示x被分为0类，重写概率公式，则
$$\omega \top x+b=ln\frac{P(Y=1|x)}{1-P(Y=1|x)}$$
$$P(Y=1|x)=\frac{1}{1+e^{-(\omega \top x+b)}}$$

2.代价函数

逻辑回归使用极大似然估计法来求解，即找到一组参数使得数据的似然度（概率）最大。
由于$P(Y=1|x)=p(x)，P(Y=0|x)=1-p(x)$
似然函数$L(\omega )=\prod [p(x_i){]}^{y_i}[1-p(x_i){]}^{1-y_i}$
为了方便求解，将两侧取对数，同时取整个数据集上的平均似然损失，则可以得到损失函数：
$$J(\omega )=-\frac{1}{N}lnL(\omega )$$

支持向量机SVM

基本思想

在二维空间内，当两类样本线性可分时，有一条直线可以将两类样本完全分隔开。扩展到高维度同样适用，只不过直线在三维会进化成平面，在更高维被称为超平面。
支持向量机的最终目的就是找到最大间隔的超平面。

详解

1.超平面方程

我们将超平面定义为$\omega \top x+b=0$，空间中的点到直线距离公式为$$d=\frac{|\omega \top x+b|}{||\omega ||}$$
令所有点中距离超平面最近的距离为$d_{min}$，
则在超平面一侧的点显然有$\omega \top x+b>0$，我们将其成为类1，即y=1，这些点满足$\omega \top x+b>||\omega ||d_{min}$；
另一侧有$\omega \top x+b<0$，我们将其称为类-1，即y=-1，这些点满足$\omega \top x+b<-||\omega ||d_{min}$。
将两个式子合并，可以得到$$\frac{y\ast (\omega \top x+b)}{||\omega ||}\ge d_{min}$$
其中$y\ast (\omega \top x+b)$被称为支持向量。
如下图所示，我们假设超平面$H_1,H_2$的方程分别为$\omega \top x+b=1,\omega \top x+b=-1$，则在$H_1,H_2$上的点是能够计算出$d_{min}$的点，此时由于支持向量经过计算的值为1，得到$$d_{min}=\frac{1}{||\omega ||}$$
我们的目标就是最大化这个值，为了方便计算，我们将最大化$\frac{1}{||\omega ||}$变成最小化$\frac{1}{2}||\omega |{|}^2$，这一步处理完全是为了简化计算，最终求出的结果是相同的。

最终，我们的最优化问题的函数为$$\min \frac{1}{2}||\omega |{|}^{2}s.t.y_i(\omega \top x_i+b)\ge 1$$

2.对偶问题与KKT条件

非常详细

3.优化方法

构造拉格朗日函数
$$\underset{\omega ,b}{\min }\underset{\lambda }{\max }L(\omega ,b,\lambda )=\frac{1}{2}||\omega |{|}^2+\sum _{i=1}^n{\lambda }_i[1-y_i(\omega x_i+b)]s.t.{\lambda }_i\ge 0$$
使用强对偶性转化成$$\underset{\lambda }{\max }\underset{\omega ,b}{\min }L(\omega ,b,\lambda )$$
对于$$\underset{\omega ,b}{\min }L(\omega ,b,\lambda )$$求偏导后，将偏导置零带入后得到结果：

显然，经过化简后的问题转化成了求：
$$\begin{gathered} \underset{\lambda }{\max }[\sum _{j=1}^n{\lambda }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\lambda }_i{\lambda }_j{y}_i{y}_j(x_i{x}_j)] \\ s.t.\sum _{i=1}^n{\lambda }_i[1-y_i(\omega x_i+b)]=0{\lambda }_i\ge 0 \end{gathered}$$
使用SMO算法每轮迭代一个参数，直至收敛，可以得到$\lambda$，通过偏导为零的条件能够计算出$\omega ,b$。

决策树

看这里

无监督学习算法

主成分分析法PCA

看这里

k-均值聚类

看这里

促进深度学习发展的挑战

维数灾难

当数据的维数很高时，很多机器学习问题变得相当困难，这种现象被称为维数灾难。

局部不变性

为了更好地泛化，机器学习方法需要由先验知识引导去学习什么类型的函数。
这些函数通常具有局部不变性，即与点A接近的点和A的性质基本一致，在k-means聚类中尤为突出。

流形学习

流形是指连接在一起的区域。正如数字8一样，其在二维空间可以被表示成一系列二元组，但在流形领域其实只是一个一维流形，只有在中心交叉点上才是二维，因此只有一部分数据才是有意义的。
流形学习就是假设数据特征中的大部分都是无效的输入，有意义的输入只分布在包含少量数据点的子集构成的流形之中。