【矩阵论笔记】最小多项式与Jordan型的关系

最新推荐文章于 2025-03-04 19:33:09 发布

番茄发烧了

最新推荐文章于 2025-03-04 19:33:09 发布

阅读量4.2w

点赞数 96

分类专栏：矩阵论

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/bless2015/article/details/105974793

版权

矩阵论专栏收录该内容

38 篇文章

订阅专栏

最小多项式

方阵A的次数最低、且首一的零化多项式称为A的最小多项式。
在这里插入图片描述

最小多项式的一般形式

在这里插入图片描述
算这个没什么办法，只能暴力计算，从m=1开始算，把A带进去是不是等0。

Jordan块的最小多项式是他的特征多项式，阶数不能再降了。

在这里插入图片描述

例题

在这里插入图片描述

$A_1$ 是一个Jordan块，他的最小多项式不将阶。

这时候 $A_2$ 的最小多项式只有两种情况，从1阶开始试。然后取最小共倍数，构成原来矩阵的最小多项式。

有了最小多项式就可以简化方阵多项式的计算。

定理：相似矩阵有相似的最小多项式
N阶方阵可对角化的充要条件是最小多项式无重根。

最小多项式与Jordan的关系

在这里插入图片描述

性质

在这里插入图片描述

上面的 $n_i$ 是代数重数，是子Jordan的阶数。
子Jordan矩阵是由Jordan块构成，Jordan块的个数是由 $\lambda_i$ 的几何重数构成 $k_i$

在这里插入图片描述
这些Jordan块的阶和最小多项式有关，最小多项式的幂就是Jordan块的阶。

例题

代数重数就是特征多项式的幂，阶数就是总的幂数之和。
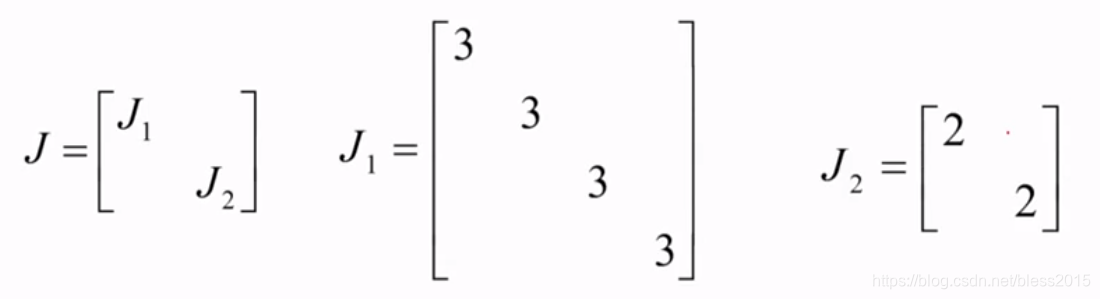
在这里插入图片描述

根据最小多项式得出子Jordan块的最高阶数

简化方阵多项式的计算

1、相似化简成对角阵
2、通过零化多项式对多项式降阶

评论 3

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。