骰子作画

最新推荐文章于 2024-03-22 19:00:13 发布

风吹夏天

最新推荐文章于 2024-03-22 19:00:13 发布

阅读量2.5k

点赞数 1

分类专栏： OpenCV C&C++ 文章标签：算法阮一峰骰子作画

本文链接：https://blog.csdn.net/bluecol/article/details/47702147

版权

OpenCV 同时被 2 个专栏收录

9 篇文章 0 订阅

订阅专栏

C&C++

5 篇文章 0 订阅

订阅专栏

阮一峰博客介绍了将图片纹理转化为骰子面的算法，通过矢量量化将图片分割并计算每个区域的灰度平均值，用1-6之间的整数表示骰子面。该算法涉及图片分割、灰度平均值计算和纹理逼近，适用于具有较好纹理的图片。代码示例展示了如何使用OpenCV实现这一过程，包括图像预处理、分割、灰度平均值计算和纹理模拟。

摘要由CSDN通过智能技术生成

阮一峰博客中描述了骰子作画算法。
这里写图片描述
思想非常简单，也就是矢量量化：将图片分成若干个区域，每个区域经过计算以后，用1-6之间的一个整数表示，代表骰子的一个面，算法总共分4步。

将图片分割成16像素x16像素的小方块。
每个小方块内共有256个像素，将每个像素点的灰度值，存入一个数组。
计算该数组的平均值，并用1-6之间的一个整数来表示。
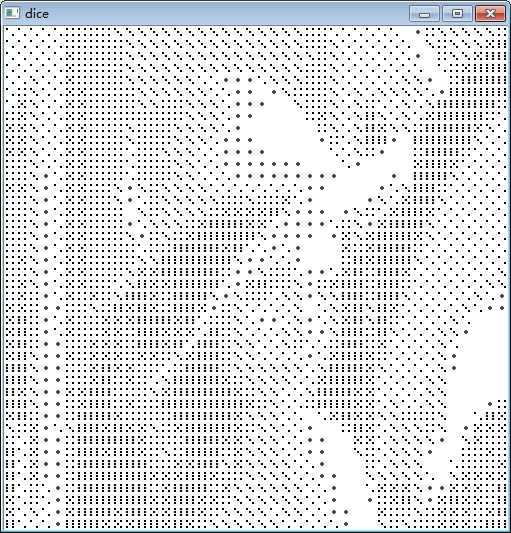
根据白点值，将骰子依次放入，就能模拟出全图

这种算法与使用的纹理密切相关，纹理越好，越是逼近，另外分割的小块越小越好。我在github上看到了haneuma0628的一个项目ImageToDice，下载下来，修改了一下，可以运行。

#include <iostream>
#include <math.h>

#include <opencv/cv.h>
#include <opencv/highgui.h>

using namespace cv;
using namespace std;

Mat trim(Mat src, int mag)
{
    int cutC, cutR;
    cutC = src.cols % mag;
    cutR = src.rows % mag;

    Mat roi;
    Size rsize(src.cols - cutC, src.rows - cutR);
    resize(src, roi, rsize, INTER_CUBIC);

    return roi;
}

Mat mozaic(Mat src)
{
    int sum = 0, mag = 12;
    Mat dst(src.size(), src.type());

    for (int y = 0; y < src.rows; y += mag)
    {
        for (int x = 0; x < src.cols; x += mag)
        {
            for (int i = 0; i < mag; i++)
            {
                for (int j = 0; j < mag; j++)
                {
                    sum += src.data[(y + i) * src.step + (x + j)];
                }
            }

            for (int i = 0; i < mag; i++)
            {
                for (int j = 0; j < mag; j++)
                {
                    dst.data[(y + i) * dst.step + (x + j)] = (int)(sum/(12*12));
                }
            }
            sum = 0;
        }
    }

    return dst;
}

int main(int argc, char *argv[])
{
    string filename = "lena.jpg";

    int cnum, rnum, mag = 12, lnum = 7;
    string fd[7];
    Mat dmat[7];

    for (int i = 0; i < lnum; i++)
        fd[i] = to_string((_ULonglong)i) + ".png";
    for (int i = 0; i < lnum; i++)
        dmat[i] = imread(fd[i], 0);

    Mat src = imread(filename, 0);
    Mat dst(src.size(), src.type());

    src = trim(src, mag);
    dst = mozaic(src);
    cnum = src.cols / mag;
    rnum = src.rows / mag;

    int *result= new int[rnum*cnum];

    Mat *himg = new Mat[cnum];
    Mat *vimg = new Mat[rnum];

    for (int y = 0; y < src.rows; y += mag)
    {
        for (int x = 0; x < src.cols; x += mag)
        {
            result[y/mag * rnum + x/mag] = dst.data[(y) * dst.step + (x)];
        }
    }

    int max = 0, min = 255;
    for (int i = 0; i < rnum; i++)
    {
        for (int j = 0; j < cnum; j++)
        {
            if (result[i*rnum+j] >= max)
                max = result[i*rnum+j];
            if (result[i*rnum+j] <= min)
                min = result[i*rnum+j];
        }
    }
    int ld;
    int level[256] = {0};
    ld = (int)((max - min) / lnum);

    int end = 0, cnt = 0;
    for (int i = max; i > min+ld; i -= ld)
    {
        for (int j = 0; j < ld; j++)
        {
            level[i-j] = cnt;
            end = i - j;
        }
        cnt++;
    }
    while (end >= min)
    {
        level[end] = 6;
        end--;
    }

    cnt=0;
    Mat vdst;
    for (int i = 0; i < rnum; i++)
    {
        for (int j = 0; j < cnum; j++)
        {
            himg[j] = imread(fd[level[result[i*rnum+j]]], 0);
        }
        hconcat(himg, cnum, vimg[i]);
    }

    vconcat(vimg, rnum, vdst);

    namedWindow("gray", CV_WINDOW_AUTOSIZE|CV_WINDOW_FREERATIO);
    imshow("gray", src);

    namedWindow("mozaic", CV_WINDOW_AUTOSIZE|CV_WINDOW_FREERATIO);
    imshow("mozaic", dst);

    namedWindow("dice", CV_WINDOW_AUTOSIZE|CV_WINDOW_FREERATIO);
    imshow("dice", vdst);

    delete[] himg;
    delete[] vimg;

    waitKey(0);
}