在传统的谱分析中,频率指的的是以傅里叶变换为基础的与时间无关的量,表示信号在一段时间内的总体特征,是一个全局性的概念。对于一般的平稳信号,传统的频域分析方法是有效的,但是在实际中往往出现得最多的是非平稳信号,其频率是随时间变化的,傅里叶频率将不再适合。为了表征这种频率随时间变换的信号的局部特征,就需要引入瞬时频率的概念。在Hilbert变换方法产生之前,瞬时频率这个概念在信号处理学科中一直存在争议,这种争议一方面是受傅里叶谱分析根深蒂固的影响;另一方面是由于对于瞬时频率的概念没有确定的定义。直到使信号解析化的Hilbert变换被提出之后,瞬时频率的定义才得以统一。
为了能够获得有意义的瞬时频率,需要一种能够将信号先行分解成一系列单分量的预处理方法。Huang等人对瞬时频率的定义进行深入研究的基础上,创造性的提出了一种新的信号分解方法—经验模式分解(Empirical Mode Decomposition,EMD)。原始信号通过该算法被分解为一系列的窄带分量,对这些分量再应用Hilbert变换,最终所求得到的瞬时频率就具有了明确的物理意义,Huang将此类信号称之为本征模态函数(Intrinsic Mode Function,IMF)或基本模式分量。
这种本征模态函数需要满足以下两个条件:
① 在整个信号序列中,极值点的个数Ne和过零点Nz的个数必须相等或最多相差不能超过一个,即:
![]()
② 在任意的时刻,分别对由局部极大值点、局部极小值点构成的上包络线
、下包络线
求和得到的局部平均值应为零,即:
![]()
满足上面两个条件的IMF,只包括一个单一的振荡模式,不存在冗余的叠加波。
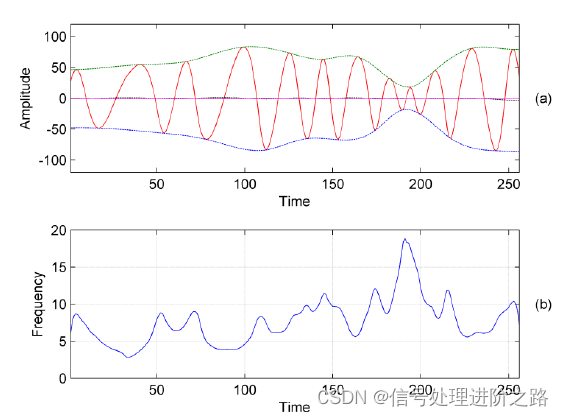
图1 典型的基本模式分量(a)及其瞬时频率(b)
对于满足基本模式分量两个限定条件的信号可以通过Hilbert变换求出其瞬时频率。但是自然界大多数信号并不是单纯的只包含一个分量,也就是说,在任何时刻信号中可能会包含多个振动模式,这也就造成了Hilbert变换无法给出一般信号的完全频率内容。基于此,EMD算法的基本思想就是获取原始信号的基本模式,接着再对基本模式进行分析以获得有意义的频率。该算法是一个迭代筛选的过程,本质上是通过数据的特征时间尺度来获得基本模式分量。
该算法的分解步骤如下:
(1) 找出原始信号x(t)的所有极值点(极大值和极小值);
(2)将全部极大值点和极小值点分别采用三次样条插值的曲线进行拟合,得到x(t)的上包络线和下包络线
;
(3) 逐点计算上包络线和下包络线的局部均值,;
(4) 原始信号x(t)减去局部均值,d(t)=x(t)-m(t);
(5)判断d(t)是否是一个基本模式分量,也即判断 d(t)是否满足上述的两个条件,如果条件满足,则将d(t)视为一个基本模式分量,c1=d(t),否则x(t)=d(t),然后重复以上操作;
(6)分解出第一个模式分量后,用x(t)减去得到剩余信号
,然后令
,重复以上过程,依次可得到
,最后剩下原始信号的余项
。

图2 信号 x(t)的上、下包络线及其均值
这样通过整个过程的分解,原始信号x(t)可以表示为:
![]()
其中为第i个基本模式分量,
为原始信号的残差,也可以解释为信号的直流分量。以上的分解过程用程序流程图可表示如下:

图3 EMD分解流程图
为了确保IMF能够保存足够的反映信号实际幅度和频率的信息,不会因过多的筛选而变成纯粹的频率调制信号,需要指定一个筛选过程的停止准则,停止的条件可以通过限制两个连线的处理结果之间的标准差Sd的大小来实现:

其中T表示信号的总长度时间,和
是筛选过程中两个连续的中间处理结果的时间序列。在筛选过程中,当
的值小于某一预先设置的值时就结束此次筛选操作,Huang建议该设定值取0.2~0.3之间。
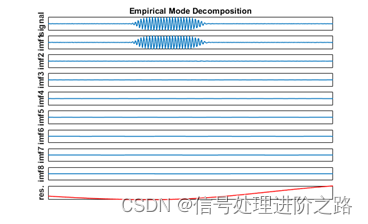
图4 EMD分解结果

图5 采用EMD算法的信号Hilbert时频谱
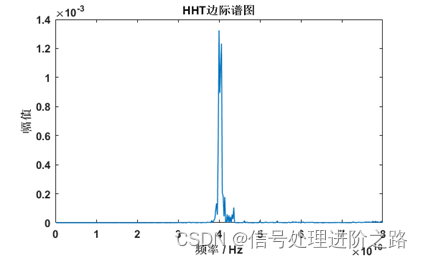
图6 信号Hilbert边际谱
























 274
274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








