Question
Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
For example,
Given:
s1 = "aabcc",
s2 = "dbbca",
When s3 = "aadbbcbcac", return true.
When s3 = "aadbbbaccc", return false.
本题难度Hard。
DP
【复杂度】
时间 O(MN) 空间 O(MN)
【题意】
开始我搞不清题目意思,还以为是分别从s1和s2中交错有规律的选取字符生成s3,实际上就是从左往右任意地从s1与s2分别选取字符,极端情况就是先取完s1的,再取s2的。
【思路】
与[LeetCode]Edit Distance比较相似,不同点在于[LeetCode]Edit Distance是一定能够完成的,而这里却要根据上一步和这一步的情况加以判断。
设f[i][j]代表分别从s1中选取了i个字符和s2中选取了j个字符后,所生成的字串能否等于s3从0到i+j-1这段的子串。可以看出来有两个途径能到达f[i][j]:
- 从
f[i-1][j]到f[i][j]。如果f[i-1][j]==false,说明上步失败了,所以这步也是失败;如果f[i-1][j]==true,这时插入的是s1[i-1],如果s1[i-1]==s3[i+j-1]才能说f[i][j]==true - 从
f[i][j-1]到f[i][j]。如果f[i][j-1]==false,说明上步失败了,所以这步也是失败;如果f[i][j-1]==true,这时插入的是s2[j-1],如果s2[j-1]==s3[i+j-1]才能说f[i][j]==true
由上面可得出状态转移方程:
【附】
DP矩阵可以用boolean矩阵。
【注意】
记得设置 f[0][0]=true;
【代码】
public class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
//require
int m=s1.length(),n=s2.length();
if(s3.length()!=m+n)
return false;
boolean[][] f=new boolean[m+1][n+1];
f[0][0]=true;
for(int i=1;i<m+1;i++)
f[i][0]=f[i-1][0]&&s1.charAt(i-1)==s3.charAt(i-1);
for(int i=1;i<n+1;i++)
f[0][i]=f[0][i-1]&&s2.charAt(i-1)==s3.charAt(i-1);
//invariant
for(int i=1;i<m+1;i++)
for(int j=1;j<n+1;j++)
f[i][j]=(f[i-1][j]&&s1.charAt(i-1)==s3.charAt(i+j-1))||
f[i][j-1]&&s2.charAt(j-1)==s3.charAt(i+j-1);
//ensure
return f[m][n];
}
}







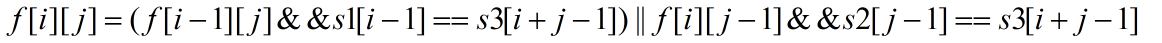














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








