Caffe对卷积层做了专门的优化,如果没有做优化的话,那么就是六层循环。所以为了做加速,卷积层需要专门的优化。
它的优化如下:
Caffe中的卷积计算是将卷积核矩阵和输入图像矩阵变换为两个大的矩阵A与B,然后A与B进行矩阵相乘得到结果C(利用GPU进行矩阵相乘的高效性),三个矩阵的说明如下:
(1)在矩阵A中
M为卷积核个数,K=k*k,等于卷积核大小,即第一个矩阵每行为一个卷积核向量(是将二维的卷积核转化为一维),总共有M行,表示有M个卷积核。
(2)在矩阵B中
N=((image_h + 2*pad_h – kernel_h)/stride_h+ 1)*((image_w +2*pad_w – kernel_w)/stride_w + 1)
image_h:输入图像的高度
image_w:输入图像的宽度
pad_h:在输入图像的高度方向两边各增加pad_h个单位长度(因为有两边,所以乘以2)
pad_w:在输入图像的宽度方向两边各增加pad_w个单位长度(因为有两边,所以乘以2)
kernel_h:卷积核的高度
kernel_w:卷积核的宽度
stride_h:高度方向的滑动步长;
stride_w:宽度方向的滑动步长。
因此,N为输出图像大小的长宽乘积,也是卷积核在输入图像上滑动可截取的最大特征数。
K=k*k,表示利用卷积核大小的框在输入图像上滑动所截取的数据大小,与卷积核大小一样大。
(3)在矩阵C中
矩阵C为矩阵A和矩阵B相乘的结果,得到一个M*N的矩阵,其中每行表示一个输出图像即feature map,共有M个输出图像(输出图像数目等于卷积核数目)
(在Caffe中是使用src/caffe/util/im2col.cu中的im2col和col2im来完成矩阵的变形和还原操作)
举个例子(方便理解):
假设有两个卷积核为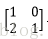
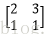
输入图像矩阵为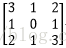
故N=[(3+2*0-2)/1+1]*[ (3+2*0-2)/1+1]=2*2=4
A矩阵(M*K)为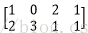
C=A*B=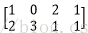
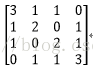
C中的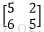
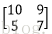
在Caffe源码中,src/caffe/util/math_functions.cu(如果使用CPU则是src/util/math_functions.cpp)中的caffe_gpu_gemm()函数,其中有两个矩阵A(M*K)
与矩阵 B(K*N),大家可以通过输出M、K、N的值即相应的矩阵内容来验证上述的原理,代码中的C矩阵与上述的C矩阵不一样,代码中的C矩阵存储的是偏置bias,
是A 与B相乘后得到M*N大小的矩阵,然后再跟这个存储偏置的矩阵C相加完成卷积过程。如果是跑Mnist训练网络的话,可以看到第一个卷积层卷积过程中,
M=20,K=25,N=24*24=576。
(caffe中涉及卷积具体过程的文件主要有:src/caffe/layers/conv_layer.cu、src/caffe/layers/base_conv_layer.cpp、 src/caffe/util/math_functions.cu、src/caffe/util/im2col.cu)
另外大家也可以参考知乎上贾扬清大神的回答,帮助理解http://www.zhihu.com/question/28385679
转载于:http://blog.csdn.net/xiaoyezi_1834/article/details/50786363









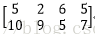














 76
76

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








