归并排序

      归并排序是一种效率较高的排序，与之前说到的三种基本排序：冒泡排序、选择排序、插入排序速度要快。归并排序核心是将归并两个有序的数组，并使它们有序的排列在数组C中。假设有两个有序数组，不要求大小长度一致，假设数组有4个数组项，数组B有6个数据项，需要将他们归并到一个数组C中，以下是归并过程。

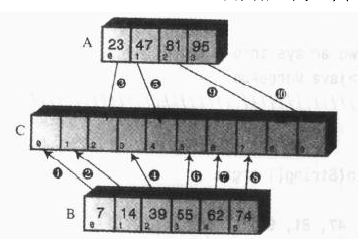
归并之后的数组C

以下是将数组A和数组B归并为数组C的代码：（前提是数组A与B有序）

//采用常规思维解决归并排序问题
//step1 构建三个数组 A B C A与B数组元素从从小到大存放在数组C里面
//比较A[n]<B[n] A[n]--->c反之亦然
//查看是否有一个数组A或B为空的情况，判断
class MergeSortNotRecursive
{
    private int[] A={1,2,3,6,9,11,16};
    private int[] B={4,5,7,8,10,18,28};
    private int[] C=new int[A.length+B.length];
    public MergeSortNotRecursive()
    {
        this.mergeSort(A, A.length, B, B.length, C);
    }
    public void mergeSort(int[] A,int Alength,int[] B,int Blength,int[] C)
    {
        int Anum=0;
        int Bnum=0;
        int Cnum=0;
        //正常的AB交替将数据放入C中
        while(Anum<Alength&&Bnum<Blength)
        {
            if(A[Anum]<B[Bnum])
            {
                C[Cnum++]=A[Anum++];
            }else
            {
                C[Cnum++]=B[Bnum++];
            }
        }
        //当出现一个数组已经排完的情况 则直接将另外一个数组从小到大排在数组C后面即可
        while(Anum<Alength)
        {
            C[Cnum++]=A[Anum++];
        }
        while(Bnum<Blength)
        {
            C[Cnum++]=B[Bnum++];
        }
        //输出数组C
        for(int m=0;m<C.length;m++)
        {
            System.out.println(C[m]);
        }
        System.out.println(C.length);
    }
}

测试结果：

1 2 3 4 5 6 7 8 9 10 11 16 18 28 14

      A数组与B数组归并到C数组的过程其实是三个while循环，第一个while循环是判断数组A与数组B进行数据比较的过程，后面两个while循环是判断哪一个数组是否出现了空，若其中一个数组已经比较完，另外一个有序数组的剩下部分直接复制到数组C后面即可。

通过递归实现归并排序

      对于一个数组进行排序的过程，利用以上排序的思想就需要把数组一分为二，分别对每一部分进行排序。对每一部分排序可以将一半都分为四分之一，对每个四分之一进行排序，之后再合并。类似每个八分之一归并为一个有序的四分之一排序，每一个十六分之一归并为八分之一排序，反复分割，直到子数组只含有一个数据项，这是基值条件。

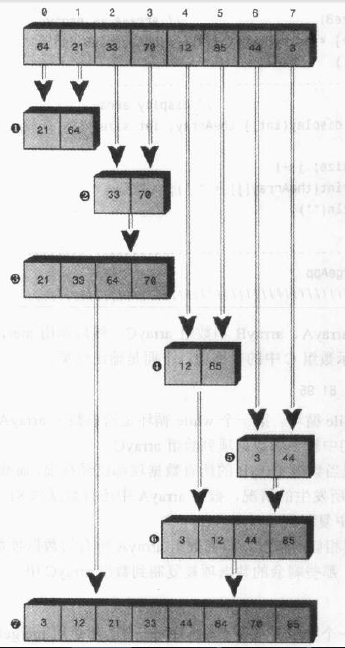
递归过程：

 //开始排序
    public void mergeSort(int[] destArray,int lowIndex,int upIndex)
    {
        if(lowIndex==upIndex)
            return;
        else
        {
            int midIndex=(lowIndex+upIndex)/2;
            //划分为左半数组
            mergeSort(destArray, lowIndex, midIndex);
            //划分右半数组
            mergeSort(destArray, midIndex+1, upIndex);
            //对数组进行归并排序
            mergeArray(destArray,lowIndex,midIndex+1,upIndex);

        }
    }

合并排序，这部分与数组A与数组B和并到数组C类同：

 //进行归并排序
    public void mergeArray(int[] destArray,int lowPtr,int higPtr,int upBounds)
    {
       int n=upBounds-lowPtr+1;
       int lowBounds=lowPtr;
       int mid=higPtr-1;
       int i=0;

       while(lowPtr<=mid&&higPtr<=upBounds)
       {
           if(array[lowPtr]<array[higPtr])
           {
               destArray[i++]=array[lowPtr++];
           }
           if(array[lowPtr]>array[higPtr])
           {
               destArray[i++]=array[higPtr++];
           }
       }
       while(lowPtr<=mid)
       {
           destArray[i++]=array[lowPtr++];
       }
       while(higPtr<=upBounds)
       {
           destArray[i++]=array[higPtr++];
       }
       for(int k=0;k<n;k++)
       {
           array[lowBounds+k]=destArray[k];
       }

    }

类中其他方法

//定义一个数组
    private int[] array=null;
    private int nItem=0;
    private int length;
    //确定数组长度
    public MergeSortRecursive(int length)
    {
        array=new int[length];
        this.length=length;

    }
    //向数组中添加数据
    public void insert(int data)
    {
        array[nItem++]=data;
    }
    //此处排序
    public void sort()
    {
        int[] destArray=new int[length];
        this.mergeSort(destArray,0,nItem-1);
        for(int i=0;i<destArray.length;i++)
        {
            System.out.println(destArray[i]);
        }

    }
    //显示数组
    public void showArray()
    {
        for (int i=0;i<array.length;i++)
        {
            System.out.print(array[i]);
        }
    }

测试类及结果：

MergeSortRecursive a=new MergeSortRecursive(10);
        a.insert(1);
        a.insert(2);
        a.insert(3);
        a.insert(6);
        a.insert(5);
        a.insert(0);
        a.insert(9);
        a.insert(8);
        a.insert(7);
        a.insert(12);
        //a.mergeSort(array, 0, 9);
        a.sort();
        a.showArray();

0 1 2 3 5 6 7 8 9 12 

关于归并排序的效率

      归并排序的时间是O（N*logN），这与之前所说的三种排序速度是要快的，归并排序的缺点是需要在内存中有另外一个大小等于被排序的数据项目的数组，如果内存较小这样就会不能工作，但是现在绝大多数硬件条件都是能够进行归并排序。