【论文阅读】Learning to Self-Train for Semi-Supervised Few-Shot Classification-CSDN博客

本文链接：https://blog.csdn.net/cainiaomyf/article/details/144615173

在这里插入图片描述

学习自我训练用于半监督小样本分类
引用：Li X, Sun Q, Liu Y, et al. Learning to self-train for semi-supervised few-shot classification[J]. Advances in neural information processing systems, 2019, 32.
论文地址：下载地址

Abstract

小样本分类（FSC）由于标注训练数据的稀缺（例如每个类别只有一个标注数据点）而具有挑战性。元学习通过学习初始化分类模型来解决小样本分类问题，已经取得了令人鼓舞的成果。本文提出了一种新颖的半监督元学习方法，称为“学习自我训练”（LST），该方法利用未标注数据，并特别元学习如何挑选和标记这些未标注数据，以进一步提高性能。为此，我们通过大量的半监督小样本任务来训练LST模型。在每个任务中，我们训练一个小样本模型来预测未标注数据的伪标签，然后在标注数据和伪标签数据上迭代自我训练步骤，每一步之后进行微调。我们还学习了一个软权重网络（SWN），用于优化伪标签的自我训练权重，使得更好的伪标签能够在梯度下降优化中发挥更大的作用。我们在两个ImageNet基准测试上评估了LST方法，取得了比现有最先进方法更大的改进。代码请访问：github.com/xinzheli1217/learning-to-self-train。

1. Introduction

今天的深度神经网络需要大量的标注数据来进行监督训练和获得最佳性能 ¹ ² ³。因此，它们在小数据领域的潜在应用是有限的。为了减少所需的数据量（例如，仅使用1-shot数据） ⁴，人们越来越关注这一问题。最强大的方法之一是元学习，通过将从相似任务中学到的经验转移到目标任务中 ⁵。在不同的元学习策略中，基于梯度下降的方法特别适合今天的神经网络 ⁵ ⁶ ⁷。另一个有趣的想法是额外使用未标注数据。使用未标注数据和相对较小的标注数据集的半监督学习方法，在标准数据集上已经取得了良好的性能 ⁸ ⁹。一种经典、直观且简单的方法是自我训练。例如，首先使用标注数据训练一个监督模型，然后基于对未标注数据的最有信心的预测（称为伪标签）扩大标注数据集 ¹⁰ ¹¹ ⁹。在标注数据稀缺时，它可以优于基于正则化的方法 ¹² ¹³ ¹⁴。

因此，本文的重点是半监督小样本分类（SSFSC）任务。具体来说，标注数据很少，而训练分类器的未标注数据要多得多。为了解决这个问题，我们提出了一种新的SSFSC方法，称为“学习自我训练”（LST），该方法成功地将一个表现良好的半监督方法（即自我训练）嵌入到元梯度下降范式中。然而，这并非易事，因为直接递归应用自我训练可能会导致逐渐漂移，从而添加噪声伪标签 ¹⁵。为了解决这个问题，我们提出了元学习一个软权重网络（SWN），自动减少噪声标签的影响，并在每次自我训练步骤后，仅使用标注数据对模型进行微调。

具体来说，我们的LST方法包括内循环自我训练（针对一个任务）和外循环元学习（针对所有任务）。LST元学习同时学习如何初始化自我训练模型，并为每个任务从噪声标签中挑选伪标签。内循环从元学习的初始化开始，这样任务特定的模型可以快速适应少量标注数据。然后，使用该模型预测伪标签，并通过元学习的软权重网络（SWN）加权标签。自我训练包括使用加权的伪标签数据重新训练，并在少量标注数据上进行微调。在外循环中，这些元学习器的性能通过独立的验证集进行评估，并使用相应的验证损失优化参数。

总结而言，我们的LST方法学习如何从SSFSC任务中积累自我监督经验，以便快速适应新的少样本任务。我们的贡献有三方面：（i）一种新颖的自我训练策略，防止模型因标签噪声而漂移，并实现稳健的递归训练。（ii）一种新颖的元学习挑选方法，优化伪标签的权重，特别是针对快速高效的自我训练。（iii）在两个版本的ImageNet基准测试（miniImageNet ¹⁶ 和 tieredImageNet ¹⁷）上进行了广泛的实验，其中我们的方法达到了顶级性能。

2. Related works

2.1 小样本分类（FSC）

大多数小样本分类（FSC）工作基于监督学习。它们大致可以分为四类：（1）基于数据增强的方法 ¹⁸ ¹⁹ ²⁰ ²¹，通过条件生成小样本类别的数据或特征；（2）度量学习方法 ¹⁶ ²² ²³，学习图像特征的相似性空间，在该空间中，分类应该在少量样本下高效进行；（3）记忆网络 ²⁴ ²⁵ ²⁶ ²⁷，设计特殊的网络来记录从已见任务中学习的“经验”，旨在将其推广到未见任务的学习中；（4）基于梯度下降的方法 ⁵ ²⁸ ²⁹ ³⁰ ³¹ ³² ³³ ⁶ ³⁴，在外循环中学习一个元学习器，用于初始化一个基础学习器，然后在新的少样本任务上进行训练。在我们的LST方法中，外循环和内循环的优化基于梯度下降方法。与以往的工作不同，我们提出了一种新颖的元学习器，为伪标签数据分配权重，特别适用于半监督小样本学习。

2.2 半监督学习（SSL）

半监督学习（SSL）方法旨在利用未标注数据获得更符合潜在数据结构的决策边界 ⁹。Π-Model应用简单的一致性正则化方法 ¹⁴，例如使用dropout、添加噪声和数据增强，其中数据会自动“标注”。Mean Teacher是Π-Model的一个更稳定版本，通过使用移动平均技术 ³⁵。Visual Adversarial Training（VAT）通过对抗扰动来正则化网络，已被证明是一种有效的正则化方法 ¹²。另一种流行的方法是熵最小化，它使用一个损失项来鼓励对未标注数据进行低熵（更有信心的）预测，无论它们的真实类别是什么 ¹³。伪标签是依赖于未标注数据预测的自监督学习方法，即伪标签 ³⁶。它可以优于基于正则化的方法，尤其是在标注数据稀缺的情况下 ⁹，这正是我们设想的情境。因此，我们在内循环训练中使用该方法。

2.3 半监督小样本分类（SSFSC）

在FSC任务中的半监督学习旨在通过在训练中加入大量未标注数据来提高分类准确性。Ren等人提出了ProtoNets的三种半监督变体 ²²，基本上使用Soft k-Means方法通过未标注数据来调节聚类中心。最近的研究使用传导传播网络（TPN） ³⁷，将标签从标注数据传播到未标注数据，并通过元学习调整TPN的关键超参数。与此不同，我们的方法基于简单的经典自我训练方法 ¹⁰ 和元梯度下降方法 ⁵ ⁶，而不需要设计新的半监督网络。Rohrbach等人 ³⁸ 提出了进一步利用外部知识（例如类别的语义属性）来解决小样本问题和零样本问题。类似地，我们希望在未来的工作中通过使用类似的外部知识来进一步提升我们方法的效果。

3. Problem definition and denotation

在传统的小样本分类（FSC）中，每个任务有一小组标注的训练数据，称为支持集 $S$ ，以及另一组未见数据用于测试，称为查询集 $Q$ 。根据[24]，我们表示另一组未标注的数据为 $R$ ，用于半监督学习（SSL）。 $R$ 可能包含或不包含干扰类的数据（不包括在 $S$ 中）。

我们的方法遵循元学习的统一情节形式 ²⁹，这与传统分类有三个方面的不同：（1）主要阶段是元训练和元测试（而不是训练和测试），每个阶段包括训练（在我们的情况下是自我训练）和测试；（2）元训练和元测试中的样本不是数据点，而是情节（在我们的情况下是SSFSC任务）；（3）元目标不是分类未见的数据点，而是快速适应新任务的分类器。让我们详细说明这些符号。给定一个用于元训练的数据集 $D$ ，我们首先从分布 $p (T)$ 中抽取SSFSC任务 ${T\}$ ，使得每个 $T$ 包含来自少数类别的少量样本，例如5个类别，每个类别1个样本。 $T$ 有一个支持集 $S$ 和一个未标注集 $R$ （具有更多样本）来训练任务特定的SSFSC模型，并且有一个查询集 $Q$ 来计算用于优化元学习器的验证损失。对于元测试，给定一个未见的新数据集 $D_{un}$ ，我们抽取一个新的SSFSC任务 $T_{un}$ 。“未见”意味着元测试任务和元训练任务之间没有图像类别（包括干扰类）重叠。我们首先初始化一个模型并为这个未见任务加权伪标签，然后在 $S_{un}$ 和 $R_{un}$ 上自我训练模型。我们在查询集 $Q_{un}$ 上评估自我训练的性能。如果有多个未见任务，我们将报告平均准确率作为最终评估。

4 Learning to self-train (LST)

应用LST到单个任务的计算流程如图1所示。它包括通过在支持集上预训练的少样本模型对未标注样本进行伪标签化；通过硬选择和软加权挑选伪标签样本；对挑选的“樱桃”进行重新训练，然后进行微调步骤；最后在查询集上进行测试。在元训练任务中，最终测试作为验证，输出用于优化LST的元学习参数的损失，如图2所示。
在这里插入图片描述图1：所提出的LST方法在单个（2类，3-shot）任务上的流程。类别的原型是该类别中样本特征的平均值，SWN为软加权网络，其优化过程在图2和第4.2节中给出。

4.1 Pseudo-labeling & cherry-picking unlabeled data

4.1.1 伪标签化

这一过程通过一个监督的小样本方法在支持集 $S$ 上训练一个任务特定的分类器 $\theta$ 。然后， $\theta$ 用来预测未标注集 $R$ 的伪标签。基本上，我们可以使用不同的方法来学习 $\theta$ 。我们选择了一种表现最佳的方法——元迁移学习（MTL） ⁶（为了公平比较，我们还将此方法作为其他半监督方法 ¹⁷ ³⁷ 的组成部分进行评估），它基于简单而优雅的梯度下降优化 ⁵。在外循环元学习中，MTL学习缩放和平移参数 $\Phi_{ss}$ ，以便快速适应一个大规模的预训练网络 $\Theta$ （例如，在miniImageNet ¹⁶ 上，64个类别，每个类别600个图像）到一个新的学习任务。在内循环基础学习中，MTL将最后的全连接层作为分类器 $\theta$ ，并用 $S$ 训练它。

接下来，我们详细介绍任务 $T$ 上的伪标签化过程。给定支持集 $S$ ，其损失用来通过梯度下降优化任务特定的基础学习器（分类器） $\theta$ ：

$\theta_t \leftarrow \theta_{t-1} - \alpha \nabla_{\theta_{t-1}} L(S; [\Phi_{ss}, \theta_{t-1}]), \quad (1)$

其中 $t$ 是迭代索引， $\in \{1, ..., T\}$ 。初始化 $\theta_0$ 由元学习得到（见第4.2节）。一旦训练完成，我们将 $\theta_T$ 与未标注样本 $R$ 一起使用，以获得伪标签 $Y_R$ ，如下所示：

$Y_R = f[\Phi_{ss}, \theta_T](R), \quad (2)$

其中 $f$ 表示具有参数 $\theta_T$ 的分类器函数和具有参数 $\Phi_{ss}$ 的特征提取器（为了简便，省略了冻结的 $\Theta$ ）。

4.1.2 挑选伪标签

由于直接在伪标签 $Y_R$ 上应用自我训练可能会导致由于标签噪声而出现逐渐漂移，我们在LST方法中提出了两种对策。第一个对策是元学习SWN，自动重新加权数据点，提升更有希望的样本的权重，并降低不太有希望的样本的权重，即学习如何挑选伪标签。在这一步之前，我们还执行硬选择，仅使用最有信心的预测 ¹¹。第二个对策是每次自我训练步骤后，仅使用标注数据（在 $S$ 中）对模型进行微调（见第4.2节）。

具体来说，我们参考 $Y_R$ 的置信度分数来挑选每个类别的前 $Z$ 个样本。因此，在这个伪标签数据集中，我们有 $ZC$ 个来自 $C$ 个类别的样本，即 $R_p$ 。在将 $R_p$ 输入到重新训练之前，我们通过元学习的软权重网络（SWN）计算它们的软权重，以减少噪声标签的影响。这些权重应该反映伪标签样本与 $C$ 个类别的表示之间的关系或距离。我们参考了一种监督学习方法RelationNets ²³，它利用支持集和查询样本之间的关系进行传统的小样本分类。

首先，我们通过平均所有样本的特征来计算每个类别的原型特征。在1-shot的情况下，我们使用唯一的样本特征作为原型。然后，给定一个伪标记样本 $(x_i, y_i) \in R_p$ ，我们将其特征与 $C$ 个原型特征连接，并将它们输入SWN。对 $c$ 类别的权重如下所示：

$w_{i,c} = f_{\Phi_{swn}} \left( [f_{\Phi_{ss}} (x_i); \sum_k f_{\Phi_{ss}} (x_{c,k})_K] \right), \quad (3)$

其中 $c$ 是类别索引， $\in [1, ..., C]$ ， $k$ 是同一类别中的样本索引， $\in [1, ..., K]$ ， $x_{c,k} \in S$ ， $\Phi_{swn}$ 表示SWN的参数，其优化过程在第4.2节中给出。注意，{w_{i,c}}已经通过SWN中的softmax层在 $C$ 个类别上进行了归一化。

4.2 Self-training on cherry-picked data

如图2（内循环）所示，我们的自我训练包含两个主要阶段。第一阶段包含在伪标签数据 $R_p$ 和支持集 $S$ 上进行几次重新训练，第二阶段则是仅使用 $S$ 的微调步骤。

在这里插入图片描述
图2：我们LST方法中的外循环和内循环训练过程。红框中的内循环包含 $m$ 步的重新训练（使用 $S$ 和 $R_p$ ）和 $T - m$ 步的微调（仅使用 $S$ ）。在递归训练中，微调后的 $\theta_T$ 替代初始的元学习得到的 $\theta_T$ （见第4.1节），用于下一阶段的伪标签化。

我们首先将分类器参数初始化为 $\theta_0 \leftarrow \theta'$ ，其中 $\theta'$ 由外循环中的先前任务元优化得到。然后，我们通过梯度下降在 $R_p$ 和 $S$ 上更新 $\theta_0$ 。假设有 $T$ 次迭代，重新训练占前 $\sim m$ 次迭代，微调占剩下的 $\sim T$ 次迭代。对于 $\in \{1, ..., m\}$ ，我们有：

$\theta_t \leftarrow \theta_{t-1} - \alpha \nabla \theta_{t-1} L(S \cup R_p; [\Phi_{swn}, \Phi_{ss}, \theta_{t-1}]), \quad (4)$

其中 $\alpha$ 是基础学习率。 $L$ 表示分类损失，对于来自不同集合的样本，其损失是不同的，如下所示：

$\cup R_p; [\Phi_{swn}, \Phi_{ss}, \theta_t]) = \begin{cases} L_{ce}(f[\Phi_{swn}, \Phi_{ss}, \theta_t](x_i), y_i), & \text{if } (x_i, y_i) \in S \\ L_{ce}(w_i f[\Phi_{swn}, \Phi_{ss}, \theta_t](x_i), y_i), & \text{if } (x_i, y_i) \in R_p \end{cases} \quad (5)$

其中 $L_{ce}$ 是交叉熵损失。对于 $S$ 中的样本，按照标准方式计算其损失。对于 $R_p$ 中的伪标签样本，在进入softmax层之前，它们的预测会通过 $w_i = \{w_{i,c}\}_{c=1}^{C}$ 进行加权。

对于 $\in \{m + 1, ..., T\}$ ， $\theta_t$ 仅在 $S$ 上进行微调：

$\theta_t \leftarrow \theta_{t-1} - \alpha \nabla \theta_{t-1} L(S; [\Phi_{swn}, \Phi_{ss}, \theta_{t-1}]), \quad (6)$

4.2.1 使用微调模型迭代自我训练

传统的自我训练通常遵循迭代过程，旨在逐渐扩展标注集 ¹⁰ ¹¹。类似地，我们的方法可以在获得微调后的模型 $\theta_T$ 后进行迭代，即使用 $\theta_T$ 在 $R$ 上预测更好的伪标签，并重新训练 $\theta$ 。有两种情景：（1） $R$ 的大小较小，例如每个类别10个样本，这样自我训练只能在相同数据上重复；（2） $R$ 的大小是无限的（至少足够大，例如每个类别100个样本），我们可以将其分成多个子集（例如10个子集，每个子集有10个样本），并每次在新的子集上进行递归学习。在本文中，我们考虑第二种情况。我们还在实验中验证了，首先划分子集，然后进行递归训练，比使用整个数据集进行一次重新训练要更好。

4.2.2 元优化Φswn, Φss 和 θ′

梯度下降基础方法通常使用 $\theta_T$ 来计算在查询集 $Q$ 上的验证损失，用于优化元学习器 ⁶ ⁵。在本文中，我们有多个元学习器，参数为 $\Phi_{swn}$ , $\Phi_{ss}$ 和 $\theta'$ 。我们提出通过在不同的自我训练阶段计算的验证损失来更新这些参数，旨在特别针对特定目的优化它们。 $\Phi_{ss}$ 和 $\theta'$ 用于特征提取和最终分类，影响整个自我训练过程。我们通过最终模型 $\theta_T$ 的损失来优化它们。而 $\Phi_{swn}$ 则产生软权重来优化重新训练步骤，它的质量应通过重新训练的分类器 $\theta_m$ 来评估。因此，我们使用 $\theta_m$ 的损失来优化它。两个优化函数如下：

$\Phi_{swn} \leftarrow \Phi_{swn} - \beta_1 \nabla \Phi_{swn} L(Q; [\Phi_{swn}, \Phi_{ss}, \theta_m]), \quad (7)$

$[\Phi_{ss}, \theta'] \leftarrow [\Phi_{ss}, \theta'] - \beta_2 \nabla [\Phi_{ss}, \theta'] L(Q; [\Phi_{swn}, \Phi_{ss}, \theta_T]), \quad (8)$

其中 $\beta_1$ 和 $\beta_2$ 是实验中手动设置的元学习率。

5. Experiments

我们在半监督设置中通过小样本图像分类准确度评估了所提的LST方法。以下我们描述了我们评估的两个基准，设置的详细信息，与最先进方法的比较，以及一项消融研究。

5.1 Datasets and implementation details

5.1.1 数据集

我们在ImageNet的两个子集上进行实验 ³⁹。miniImageNet最初由Vinyals等人提出 ¹⁶，并已广泛应用于监督小样本分类（FSC）工作 ⁵ ³⁰ ⁶ ⁷ ³² ⁴⁰，以及半监督工作 ³⁷ ¹⁷。总共有100个类别，每个类别600个84×84的彩色图像。在统一设置下，这些类别分别被划分为64、16和20个类别用于元训练、元验证和元测试。tieredImageNet由Ren等人提出 ¹⁷，包含比miniImageNet更多的类别，共608个类别，这些类别来自34个超级类别，划分为20个类别用于元训练（351个类别），6个类别用于元验证（97个类别），8个类别用于元测试（160个类别）。每个类别的平均图像数量为1281，比miniImageNet上的要大得多。所有图像被调整为84×84。在这两个数据集上，我们遵循以前工作中使用的半监督任务划分方法 ¹⁷ ³⁷。我们考虑5-way分类，样本为5-way, 1-shot（5-shot）任务，包含1（5）个样本作为支持集 $S$ ，并且有15个样本（统一数量）作为查询集 $Q$ 。然后，在1-shot（5-shot）任务中，我们有每个类别30（50）个未标注图像作为未标注集 $R$ 。经过硬选择后，我们筛选出10（20）个样本，并仅使用其余20（30）个有信心的样本进行软加权，然后进行重新训练。在递归训练中，我们使用一个更大的未标注数据池，其中包含100个样本，每次迭代时，我们可以从中采样一定数量的样本，即1-shot（5-shot）任务为30（50）个样本。

5.1.2 网络架构

Θ和Φss的网络架构基于ResNet-12（详见MTL ⁶），它由4个残差块组成，每个块包含3个3×3卷积层。在每个块的末尾应用一个2×2的最大池化层。滤波器的数量从64开始，并在下一个块中翻倍。在残差块后，应用均值池化层将特征图压缩为512维的嵌入。SWN的架构由2个3×3卷积层组成，每个卷积层有64个滤波器，之后是2个全连接层，维度分别为8和1。

5.1.3 超参数

我们遵循MTL ⁶中使用的设置。基础学习率 $\alpha$ （在公式1、4和6中）设置为0.01。元学习率 $\beta_1$ 和 $\beta_2$ （在公式7和8中）初始设置为0.001，并且每1000次元迭代衰减为原来的一半，直到最小值0.0001为止。我们使用2的元批次大小，运行15000次元迭代。在递归训练中，我们对1-shot（5-shot）任务使用6（3）个递归阶段。每个递归阶段包含10次重新训练和30次微调步骤。

5.1.4 比较方法

在SSFSC方面，我们有两种方法进行比较，即Soft Masked k-Means ¹⁷和TPN ³⁷。它们的原始模型使用浅层的4CONV ⁵从头开始训练，用于特征提取。为了公平比较，我们将MTL作为它们模型的一个组件，以使用更深的网络和预训练模型，这些模型已被证明更有效。此外，我们在实验中使用最大未标注数据预算，即每个类别100个样本。我们还将与最先进的监督FSC模型进行比较，这些模型与我们的方法密切相关。它们基于数据增强 ¹⁸ ¹⁹ 或梯度下降 ⁵ ³⁰ ³² ⁴⁰ ³³ ⁴¹ ⁷ ⁶ ⁴²。

5.1.5 消融设置

为了展示我们LST方法的有效性，我们设计了以下两组设置：有和没有元训练。以下是详细的消融设置。no selection表示一次自我训练的基准，不选择伪标签。hard表示伪标签的硬选择。hard with meta-training表示仅对[Φss, θT]进行元学习。soft表示通过元学习的SWN对选定的伪标签进行软加权。recursive表示基于微调模型的多次自我训练，见第4.2节。请注意，这个recursive只适用于元测试任务，因为元学习的SWN可以被重复使用。我们还有一个与recursive类似的设置，称为mixing，其中我们混合在recursive中使用的所有未标注子集，并且只进行一次重新训练（见第4.2节倒数第二段）。

5.2 Results and analyses

我们在半监督小样本分类（SSFSC）任务上进行了广泛的实验。在表1中，我们分别展示了与最先进的小样本分类（FSC）方法在miniImageNet和tieredImageNet上的比较结果。在表2中，我们提供了消融设置的实验结果以及与最先进的SSFSC方法的比较。在图3中，我们展示了使用不同数量的重新训练步骤（即图2中的 $m$ 变化）的效果。

表1：在miniImageNet和tieredImageNet数据集上的5-way, 1-shot和5-shot分类准确率（%）。 “pre” 表示使用所有训练数据点为单一分类任务预训练的模型。请注意，这是一个参考表，用于展示通过考虑未标注数据所获得的性能提升。
在这里插入图片描述

5.2.1 两个数据集的FSC方法概览

在表1的上半部分，我们展示了miniImageNet上的SSFSC结果。可以看出，LST在1-shot（70.1%）设置中相比于所有其他FSC方法取得了最佳性能。此外，它在5-shot任务中达到78.7%的准确率，这一结果略好于使用各种正则化技术（如数据增强和标签平滑）的方法 ⁴² 报告的78.6%。与基线方法MTL ⁶相比，LST在1-shot和5-shot设置下分别提高了8.9%和3.2%的准确率，这证明了LST在利用未标注数据时的效率。

在表1的下半部分，我们展示了tieredImageNet上的结果。我们的LST在1-shot（77.7%）和5-shot（85.2%）设置中均表现最佳，并且分别比最先进的方法 ⁴² 提高了11.7%和3.6%。与MTL ⁶相比，LST在1-shot和5-shot设置下分别提高了12.1%和6.6%的准确率。

5.2.2 硬选择

从表2中可以看出，硬选择策略通常会带来改进。例如，与无选择相比，硬选择在miniImageNet上的1-shot和5-shot准确率分别提升了3.3%和1.1%，在tieredImageNet上分别提升了2.4%和0.4%。这是因为选择更可靠的样本可以缓解由噪声标签带来的干扰。此外，简单重复这一策略（recursive, hard）平均带来了1%的增益。

表2：在miniImageNet（“mini”）和tieredImageNet（“tiered”）上的消融设置（中间部分）和相关SSFSC工作的分类准确率（%）（底部部分）。 “fully supervised” 表示使用了未标注数据的标签。 "w/D"表示使用了来自支持集中排除的3个干扰类的未标注数据 ³⁷ ¹⁷。使用每类5个样本的小型未标注集的结果 ¹⁷ 提供在补充材料中。
在这里插入图片描述

5.2.3 SWN

元学习的SWN能够以软方式减少噪声预测的影响，从而带来更好的性能。当单独使用SWN时，soft在性能上与两个以前的SSFSC方法¹⁷ ³⁷相当。当SWN与硬选择结合使用（hard, soft）时，相比于hard(Φss, θ′)，在miniImageNet的1-shot和5-shot上均提升了0.9%，这表明SWN和硬选择策略是互补的。

5.2.4 递归自我训练

将recursive, hard与hard相比，可以看出，通过递归自我训练更新 $\theta$ 时，无论是在"meta"还是"no meta"场景中，性能都有所提高。例如，在miniImageNet的1-shot任务中，应用递归训练到hard, soft提升了5.1%。然而，当使用mixing, hard, soft（在没有递归的情况下学习所有未标注数据）时，提升减少了3.9%。这些观察表明，递归自我训练能够成功利用未标注样本。但在包含干扰类的情况下，该方法有时会带来不良结果。例如，与hard相比，recursive, hard在miniImageNet和tieredImageNet的1-shot任务中分别减少了0.4%和0.5%，这可能是由于早期递归阶段的干扰传播到后期阶段所致。

5.2.5 与最先进的SSFSC方法的比较

可以看出，Masked Soft k-Means¹⁷和TPN³⁷在使用MTL并加入更多未标注样本（每类100个）后，其性能有了大幅提升（1-shot超过10%，5-shot超过7%）。与这些方法相比，我们的方法（recursive, hard, soft）在miniImageNet上分别在1-shot和5-shot任务中取得了7.4%和4.5%的提升。在tieredImageNet上，我们的方法也分别比TPN高出5.6%和1.9%。尽管在将干扰类加入未标注数据集时，我们的方法受到的影响略大，但相比于其他方法，我们仍然取得了最佳结果。

5.2.6 递归训练步骤的数量

在图3中，我们展示了不同递归训练步骤的结果。图3(a)、(b)和©分别显示了三种设置：LST；使用现成MTL方法的recursive, hard；以及将MTL替换为预训练ResNet-12模型的recursive, hard。所有三种情况均表明，重新训练确实带来了更好的结果，但过多的重新训练步骤可能导致漂移问题并对性能产生副作用。前两种设置在10次重新训练时达到最佳性能，而第三种设置需要20次。这表明基于MTL的方法（LST和recursive, hard）相比直接使用预训练ResNet-12模型的方法收敛更快。
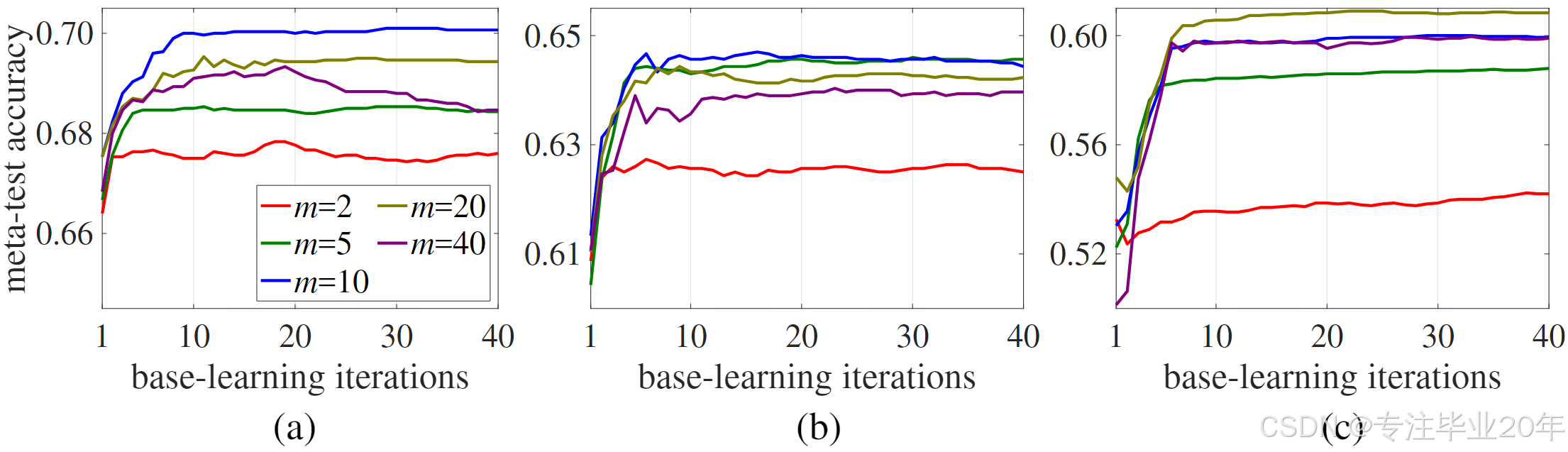
在这里插入图片描述
图3：在1-shot miniImageNet上使用不同重新训练步骤的分类准确率。例如， $m = 2$ 表示每个递归阶段使用2步重新训练和38步（总共40步）微调。每条曲线显示在最终阶段获得的结果。方法包括： (a) 我们的LST方法； (b) recursive, hard（无元学习）与MTL ⁶； © recursive, hard（无元学习），仅通过预训练ResNet-12模型初始化 ⁶。 tieredImageNet上的结果提供在补充材料中。

5.2.7 干扰类数量的定量分析

在图4中，我们展示了干扰类对我们的LST和相关方法（使用MTL改进版）¹⁷ ³⁵的影响。更多的干扰类会导致所有方法的性能下降。在最困难的7个干扰类场景中，我们的LST表现最佳，比TPN³⁷高出超过2%。在我们的不同设置中，可以看出，使用较少递归训练步骤（即较小的 $m$ ）的LST在减少更多干扰类的影响时效果更好。

在这里插入图片描述
图4：在miniImageNet 1-shot (a) 和 tieredImageNet 1-shot (b) 上，使用不同数量干扰类的分类准确率。

5.2.8 伪标签的性能

以miniImageNet 1-shot任务为例，我们记录了在meta-training和meta-test阶段伪标签的准确率（基于我们最好的方法recursive, hard, soft），分别在表3和表4中给出。在meta-training中，可以看到准确率从47.0%（iter=0）增长到71.5%（iter=15k），并在2k次迭代后趋于饱和。在meta-test中，有6个递归阶段。从阶段2到阶段6，使用我们最佳方法的600个meta-test任务的平均准确率从59.8%提高到68.8%。

表3： 在miniImageNet 1-shot任务上，元训练过程中的伪标签准确率（%）。
在这里插入图片描述
表4： 在miniImageNet 1-shot任务上，元测试的六个递归阶段中的伪标签准确率（%）。Stage-1为初始化阶段。

5.2.9 泛化能力

我们的LST方法原则上能够泛化到其他基于优化的FSC方法。为了验证这一点，我们用一种经典方法MAML⁵替换了MTL。我们进行了基于MAML的LST实验（使用recursive, hard, soft）并与相同4CONV架构模型的TPN³⁷进行比较。在miniImageNet的1-shot任务中，我们的方法的准确率为54.8%（带干扰类为52.0%），分别比TPN高出2.0%（带干扰类高1.6%）。在更具挑战性的tieredImageNet（1-shot）数据集上，我们的方法表现出更高的优势，即2.9%（带干扰类高2.0%）。

6. Conclusions

我们提出了一种新颖的LST方法，用于半监督小样本分类。提出了一种基于递归学习的自我训练策略，以实现内循环的稳健收敛；同时，通过元学习一个挑选网络来选择并标记外循环中优化的未标注数据。我们的方法具有通用性，因为可以在不同基础学习器架构下，结合任何基于优化的小样本方法。在两个流行的小样本基准上，我们的方法在最先进的FSC和SSFSC方法上都实现了稳定的性能提升。

LeCun Yann, Bengio Yoshua, and Hinton Geoffrey. Deep learning. Nature, 521(7553):436, 2015. ↩︎
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016. ↩︎
Evan Shelhamer, Jonathan Long, and Trevor Darrell. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell., 39(4):640–651, 2017. ↩︎
Fei-Fei Li, Robert Fergus, and Pietro Perona. One-shot learning of object categories. IEEE Trans. Pattern Anal. Mach. Intell., 28(4):594–611, 2006. ↩︎
Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation of deep networks. In ICML, 2017. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Qianru Sun, Yaoyao Liu, Tat-Seng Chua, and Bernt Schiele. Meta-transfer learning for few-shot learning. In CVPR, 2019. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Andrei A. Rusu, Dushyant Rao, Jakub Sygnowski, Oriol Vinyals, Razvan Pascanu, Simon Osindero, and Raia Hadsell. Meta-learning with latent embedding optimization. In ICLR, 2019. ↩︎ ↩︎ ↩︎
Chapelle Olivier, Schölkopf Bernhard, and Zien Alexander. Semi-supervised learning, volume ISBN 978-0-262-03358-9. Cambridge, Mass.: MIT Press, 2006. ↩︎
Avital Oliver, Augustus Odena, Colin A. Raffel, Ekin Dogus Cubuk, and Ian J. Goodfellow. Realistic evaluation of deep semi-supervised learning algorithms. In NeurIPS, 2018. ↩︎ ↩︎ ↩︎ ↩︎
David Yarowsky. Unsupervised word sense disambiguation rivaling supervised methods. In ACL, 1995. ↩︎ ↩︎ ↩︎
Isaac Triguero, Salvador García, and Francisco Herrera. Self-labeled techniques for semi-supervised learning: taxonomy, software and empirical study. Knowl. Inf. Syst., 42(2):245–284, 2015. ↩︎ ↩︎ ↩︎
Takeru Miyato, Andrew M. Dai, and Ian J. Goodfellow. Virtual adversarial training for semi-supervised text classification. arXiv, 1605.07725, 2016. ↩︎ ↩︎
Yves Grandvalet and Yoshua Bengio. Semi-supervised learning by entropy minimization. In NIPS, 2004. ↩︎ ↩︎
Samuli Laine and Timo Aila. Temporal ensembling for semi-supervised learning. In ICLR, 2017. ↩︎ ↩︎
Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. In ICLR, 2017. ↩︎
Oriol Vinyals, Charles Blundell, Tim Lillicrap, Koray Kavukcuoglu, and Daan Wierstra. Matching networks for one shot learning. In NIPS, 2016. ↩︎ ↩︎ ↩︎ ↩︎
Mengye Ren, Eleni Triantafillou, Sachin Ravi, Jake Snell, Kevin Swersky, Joshua B. Tenenbaum, Hugo Larochelle, and Richard S. Zemel. Meta-learning for semi-supervised few-shot classification. In ICLR, 2018. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Akshay Mehrotra and Ambedkar Dukkipati. Generative adversarial residual pairwise networks for one shot learning. arXiv, 1703.08033, 2017. ↩︎ ↩︎
Eli Schwartz, Leonid Karlinsky, Joseph Shtok, Sivan Harary, Mattias Marder, Rogério Schmidt Feris, Abhishek Kumar, Raja Giryes, and Alexander M. Bronstein. Delta-encoder: an effective sample synthesis method for few-shot object recognition. In NeurIPS, 2018. ↩︎ ↩︎
Yu-Xiong Wang, Ross B. Girshick, Martial Hebert, and Bharath Hariharan. Low-shot learning from imaginary data. In CVPR, 2018. ↩︎
Yongqin Xian, Saurabh Sharma, Bernt Schiele, and Zeynep Akata. f-VAEGAN-D2: A feature generating framework for any-shot learning. In CVPR, 2019. ↩︎
Jake Snell, Kevin Swersky, and Richard S. Zemel. Prototypical networks for few-shot learning. In NIPS, 2017. ↩︎ ↩︎
Flood Sung, Yongxin Yang, Li Zhang, Tao Xiang, Philip H. S. Torr, and Timothy M. Hospedales. Learning to compare: Relation network for few-shot learning. In CVPR, 2018. ↩︎ ↩︎
Tsendsuren Munkhdalai and Hong Yu. Meta networks. In ICML, 2017. ↩︎
Adam Santoro, Sergey Bartunov, Matthew Botvinick, Daan Wierstra, and Timothy P. Lillicrap. Meta-learning with memory-augmented neural networks. In ICML, 2016. ↩︎
Boris N. Oreshkin, Pau Rodríguez, and Alexandre Lacoste. TADAM: task dependent adaptive metric for improved few-shot learning. In NeurIPS, 2018. ↩︎
Nikhil Mishra, Mostafa Rohaninejad, Xi Chen, and Pieter Abbeel. Snail: A simple neural attentive meta-learner. In ICLR, 2018. ↩︎
Chelsea Finn, Kelvin Xu, and Sergey Levine. Probabilistic model-agnostic meta-learning. In NeurIPS, 2018. ↩︎
Antreas Antoniou, Harrison Edwards, and Amos Storkey. How to train your maml. In ICLR, 2019. ↩︎ ↩︎
Sachin Ravi and Hugo Larochelle. Optimization as a model for few-shot learning. In ICLR, 2017. ↩︎ ↩︎ ↩︎
Yoonho Lee and Seungjin Choi. Gradient-based meta-learning with learned layerwise metric and subspace. In ICML, 2018. ↩︎
Erin Grant, Chelsea Finn, Sergey Levine, Trevor Darrell, and Thomas L. Griffiths. Recasting gradient-based meta-learning as hierarchical bayes. In ICLR, 2018. ↩︎ ↩︎ ↩︎
Ruixiang Zhang, Tong Che, Zoubin Ghahramani, Yoshua Bengio, and Yangqiu Song. Metagan: An adversarial approach to few-shot learning. In NeurIPS, 2018. ↩︎ ↩︎
Yaoyao Liu, Yuting Su, An-An Liu, Tat-Seng Chua, Bernt Schiele, and Qianru Sun. Lcc: Learning to customize and combine neural networks for few-shot learning. arXiv, 1904.08479, 2019. ↩︎
Antti Tarvainen and Harri Valpola. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In NIPS, 2017. ↩︎ ↩︎
Lee Dong-Hyun. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In ICML Workshops, 2013. ↩︎
Yanbin Liu, Juho Lee, Minseop Park, Saehoon Kim, and Yi Yang. Transductive propagation network for few-shot learning. In ICLR, 2019. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Marcus Rohrbach, Sandra Ebert, and Bernt Schiele. Transfer learning in a transductive setting. In NIPS, 2013. ↩︎
Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision, 115(3):211–252, 2015. ↩︎
Luca Franceschi, Paolo Frasconi, Saverio Salzo, Riccardo Grazzi, and Massimiliano Pontil. Bilevel programming for hyperparameter optimization and meta-learning. In ICML, 2018. ↩︎ ↩︎
Tsendsuren Munkhdalai, Xingdi Yuan, Soroush Mehri, and Adam Trischler. Rapid adaptation with conditionally shifted neurons. In ICML, 2018. ↩︎
Kwonjoon Lee, Subhransu Maji, Avinash Ravichandran, and Stefano Soatto. Meta-learning with differentiable convex optimization. In CVPR, 2019. ↩︎ ↩︎ ↩︎