三、归纳法
当我们要解决一个问题的时候,可以先分析这个问题的几种简单的、特殊的情况,从中发现并归纳出一般规律或作出某种猜想,从而找到解决问题的途径。这种从特殊到一般的思维方法称为归纳法。
例10 将100以内的质数从小到大排成一个数字串,依次完成以下5项工作叫做一次操作:
(1)将左边第一个数码移到数字串的最右边;
(2)从左到右两位一节组成若干个两位数;
(3)划去这些两位数中的合数;
(4)所剩的两位质数中有相同者,保留左边的一个,其余划去;
(5)所余的两位质数保持数码次序又组成一个新的数字串。
问:经过1999次操作,所得的数字串是什么?
解:第1次操作得数字串711131131737;
第2次操作得数字串11133173;
第3次操作得数字串111731;
第4次操作得数字串1173;
第5次操作得数字串1731;
第6次操作得数字串7311;
第7次操作得数字串3117;
第8次操作得数字串1173。
不难看出,后面以4次为周期循环,1999=4×499+3,所以第1999次操作所得数字串与第7次相同,是3117。
例11 有100张的一摞卡片,玲玲拿着它们,从最上面的一张开始按如下的顺序进行操作:把最上面的第一张卡片舍去,把下一张卡片放在这一摞卡片的最下面。再把原来的第三张卡片舍去,把下一张卡片放在最下面。反复这样做,直到手中只剩下一张卡片,那么剩下的这张卡片是原来那一摞卡片的第几张?
分析与解:可以从简单的不失题目性质的问题入手,寻找规律。列表如下:
设这一摞卡片的张数为N,观察上表可知:
(1)当N=2a(a=0,1,2,3,…)时,剩下的这张卡片是原来那一摞卡片的最后一张,即第2a张;
(2)当N=2a+m(m<2a)时,剩下的这张卡片是原来那一摞卡片的第2m张。
取N=100,因为100=26+36,2×36=72,所以剩下这张卡片是原来那一摞卡片的第72张。
说明:此题实质上是著名的约瑟夫斯问题:
传说古代有一批人被蛮族俘虏了,敌人命令他们排成圆圈,编上号码1,2,3,…然后把1号杀了,把3号杀了,总之每隔一个人杀一个人,最后剩下一个人,这个人就是约瑟夫斯。如果这批俘虏有111人,那么约瑟夫斯的号码是多少?
四、反证法
反证法即首先对命题的结论作出相反的假设,并从此假设出发,经过正确的推理,导出矛盾的结果,这就否定了作为推理出发点的假设,从而肯定了原结论是正确的。
反证法的过程可简述为以下三个步骤:
1.反设:假设所要证明的结论不成立,而其反面成立;
2.归谬:由“反设”出发,通过正确的推理,导出矛盾――与已知条件、公理、定义、定理、反设及明显的事实矛盾或自相矛盾;
3.结论:因为推理正确,产生矛盾的原因在于“反设”的谬误,既然结论的反面不成立,从而肯定了结论成立。
运用反证法的关键在于导致矛盾。在数论中,不少问题是通过奇偶分析或同余等方法引出矛盾的。
解:如果存在这样的三位数,那么就有
100a+10b+c=(10a+b)+(10b+c)+(10a+c)。上式可化简为 80a=b+c,而这显然是不可能的,因为a≥1,b≤9,c≤9。这表明所找的数是不存在的。
说明:在证明不存在性的问题时,常用反证法:先假设存在,即至少有一个元素,它符合命题中所述的一切要求,然后从这个存在的元素出发,进行推理,直到产生矛盾。
例2 将某个17位数的数字的排列顺序颠倒,再将得到的数与原来的数相加。试说明,得到的和中至少有一个数字是偶数。
解:假设得到的和中没有一个数字是偶数,即全是奇数。在如下式所示的加法算式中,末一列数字的和d+a为奇数,从而第一列也是如此,因此第二列数字的和b+c≤9。将已知数的前两位数字a,b与末两位数字c,d去掉,所得的13位数仍具有“将它的数字颠倒,得到的数与它相加,和的数字都是奇数”这一性质。照此进行,每次去掉首末各两位数字,最后得到一位数,它与自身相加是偶数,矛盾。故和的数字中必有偶数。
说明:显然结论对(4k+1)位数也成立。但对其他位数的数不一定成立。如12+21,506+605等。
例3 有一个魔术钱币机,当塞入1枚1分硬币时,退出1枚1角和1枚5分的硬币;当塞入1枚5分硬币时,退出4枚1角硬币;当塞入1枚1角硬币时,退出3枚1分硬币。小红由1枚1分硬币和1枚5分硬币开始,反复将硬币塞入机器,能否在某一时刻,小红手中1分的硬币刚好比1角的硬币少10枚?
解:开始只有1枚1分硬币,没有1角的,所以开始时1角的和1分的总枚数为 0+1=1,这是奇数。每使用一次该机器,1分与1角的总枚数记为Q。下面考查Q的奇偶性。
如果塞入1枚1分的硬币,那么Q暂时减少1,但我们取回了1枚1角的硬币(和1枚5分的硬币),所以总数Q没有变化;如果再塞入1枚5分的硬币(得到4枚1角硬币),那么Q增加4,而其奇偶性不变;如果塞入1枚1角硬币,那么Q增加2,其奇偶性也不变。所以每使用一次机器,Q的奇偶性不变,因为开始时Q为奇数,它将一直保持为奇数。
这样,我们就不可能得到1分硬币的枚数刚好比1角硬币数少 10的情况,因为如果我们有P枚1分硬币和(P+10)枚1角硬币,那么1分和1角硬币的总枚数为(2P+10),这是一个偶数。矛盾。
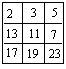
例 4在3×3的方格表中已如右图填入了9个质数。将表中同一行或同一列的3个数加上相同的自然数称为一次操作。问:你能通过若干次操作使得表中9个数都变为相同的数吗?为什么?
解:因为表中9个质数之和恰为100,被3除余1,经过每一次操作,总和增加3的倍数,所以表中9个数之和除以3总是余1。如果表中9个数变为相等,那么9个数的总和应能被3整除,这就得出矛盾!
所以,无论经过多少次操作,表中的数都不会变为9个相同的数。
五、构造法
构造法是一种重要的数学方法,它灵活多样,数论中的许多问题都可以通过构造某些特殊结构、特殊性质的整数或整数的组合来解决。
例5 9999和99!能否表示成为99个连续的奇自然数之和?
解:9999能。因为9999等于99个9998之和,所以可以直接构造如下:
9999=(9998-98)+(9998-96)+…+
=(9998-2)+9998+(9998+2)+…+
=(9998+96)+(9998+98)。
99!不能。因为99!为偶数,而99个奇数之和为奇数,所以99!不能表示为99个连续奇数之和。
说明:利用构造法证明存在性问题,只要把满足题设要求的数学对象构造出来就行。
例6 从1,2,3,…,999这999个数中,要求划去尽量少的数,使得余下的数中每一个数都不等于另外两个数的乘积。应划去哪些数?
解:我们可划去2,3,…,30,31这30个数,因为划去了上述这30个数之后,余下的数中,除1以外的任何两个数之积将大于322=1024>999。
另一方面,可以通过构造三元数组来证明30是最少的个数。
(2,61,2×61),(3,60,3×60),(4,59,4×59),…,
(30,33,30×33),(31,32,31×32)。
上面写出的这些数都是互不相同的,并且这些数中的最大数为 31×32=992。如果划去的数少于30个,那么上述三元数组至少剩下一个,这样就不满足题设条件。所以,30是最少的个数。
六、配对法
配对的形式是多样的,有数字的凑整配对,也有集合间元素与元素的配对(可用于计数)。传说高斯8岁时求和(1+2+…+100)首创了配对。像高斯那样,善于使用配对技巧,常常能使一些表面上看来很麻烦,甚至很棘手的问题迎刃而解。
例7 求1,2,3,…,9999998,9999999这9999999个数中所有数码的和。
解:在这些数前面添一个数0,并不影响所有数码的和。将这1000万个数两两配对,因为0与9999999,1与9999998,…,4999999与5000000各对的数码和都是9×7=63。这里共有5000000对,故所有数码的和是63×5000000=315000000。
例8 某商场向顾客发放9999张购物券,每张购物券上印有一个四位数的号码,从0001到9999号。若号码的前两位数字之和等于后两位数字之和,则称这张购物券为“幸运券”。例如号码 0734,因 0+7=3+4,所以这个号码的购物券是幸运券。试说明,这个商场所发的购物券中,所有幸运券的号码之和能被101整除。
解:显然,号码为9999的是幸运券,除这张幸运券外,如果某个号码n是幸运券,那么号码为m=9999-n的购物券也是幸运券。由于9999是奇数,所以m≠n。
由于m+n=9999,相加时不出现进位,所以除去号码是9999这张幸运券之外,其余所有幸运券可全部两两配对,而每一对两个号码之和均为9999,即所有幸运券号码之和是9999的倍数。
因为9999=99×101,所以所有幸运券号码之和能被101整除。
试说明分子m是质数89的倍数。
解法一:仿照高斯求和(1+2+3+…+n)的办法,将和
①②两式相加,得
从而
2m×88!=89×k(k是正整数)。
因为89为奇质数,所以89不能整除 88!,从而89|m。
解法二:作配对处理
将括号内的分数进行通分,其公分母为
1×88×2×87×3×86×…×44×45=88!,
从而
m×88!=89×k(k=n×q)。
因为89为奇质数,所以89不能整除88!,从而89|m。
七、估计法
估计法是用不等式放大或缩小的方法来确定某个数或整个算式的取值范围,以获取有关量的本质特征,达到解题的目的。
在数论问题中,一个有限范围内的整数至多有有限个,过渡到整数,就能够对可能的情况逐一检验,以确定问题的解。

解:因每一真分数满足
而所求的数整S是四个不同的真分数之和,因此2<S<4,推知S=3。于是可得如下5组不同的真分数:
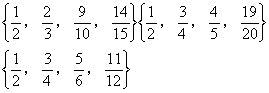
例11 已知在乘积1×2×3×…×n的尾部恰好有106个连续的零,求自然数n的最大值。
分析:若已知n的具体数值,求1×2×…×n的尾部零的个数,则比较容易解决,现在反过来知道尾部零的个数,求n的值,不大好处理,我们可以先估计n大约是多少,然后再仔细确定n的值。
因此,乘积1×2×3×…×400中含质因数5的个数为80+16+3=99(个)。又乘积中质因数2的个数多于5的个数,故n=400时,1×2×…×n的尾部有99个零,还需 7个零,注意到425中含有2个质因数5,所以
当n=430时,1×2×…×n的尾部有106个零;
当n=435时,1×2×…×n的尾部有107个零。
因此,n的最大值为434。









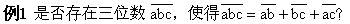
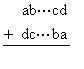
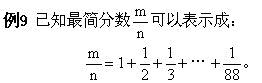
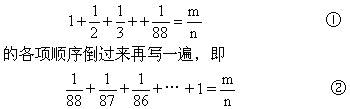
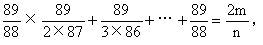
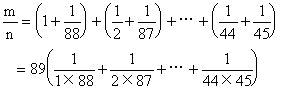
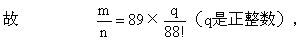
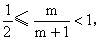
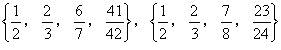

















 845
845

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








