数论是研究整数性质的一个数学分支,它历史悠久,而且有着强大的生命力。数论问题叙述简明,“很多数论问题可以从经验中归纳出来,并且仅用三言两语就能向一个行外人解释清楚,但要证明它却远非易事”。因而有人说:“用以发现天才,在初等数学中再也没有比数论更好的课程了。任何学生,如能把当今任何一本数论教材中的习题做出,就应当受到鼓励,并劝他将来从事数学方面的工作。”所以在国内外各级各类的数学竞赛中,数论问题总是占有相当大的比重。
数学竞赛中的数论问题,常常涉及整数的整除性、带余除法、奇数与偶数、质数与合数、约数与倍数、整数的分解与分拆。主要的结论有:
1.带余除法:若a,b是两个整数,b>0,则存在两个整数q,r,使得
a=bq+r(0≤r<b),
且q,r是唯一的。
特别地,如果r=0,那么a=bq。这时,a被b整除,记作b|a,也称b是a的约数,a是b的倍数。
2.若a|c,b|c,且a,b互质,则ab|c。
3.唯一分解定理:每一个大于1的自然数n都可以写成质数的连乘积,即
其中p1<p2<…<pk为质数,a1,a2,…,ak为自然数,并且这种表示是唯一的。(1)式称为n的质因数分解或标准分解。
4.约数个数定理:设n的标准分解式为(1),则它的正约数个数为:
d(n)=(a1+1)(a2+1)…(ak+1)。
5.整数集的离散性:n与n+1之间不再有其他整数。因此,不等式x<y与x≤y-1是等价的。
下面,我们将按解数论题的方法技巧来分类讲解。
一、利用整数的各种表示法
对于某些研究整数本身的特性的问题,若能合理地选择整数的表示形式,则常常有助于问题的解决。这些常用的形式有:
1.十进制表示形式:n=an10n+an-110n-1+…+a0;
2.带余形式:a=bq+r;
4.2的乘方与奇数之积式:n=2mt,其中t为奇数。
例1 红、黄、白和蓝色卡片各1张,每张上写有1个数字,小明将这4张卡片如下图放置,使它们构成1个四位数,并计算这个四位数与它的各位数字之和的10倍的差。结果小明发现,无论白色卡片上是什么数字,计算结果都是1998。问:红、黄、蓝3张卡片上各是什么数字?
解:设红、黄、白、蓝色卡片上的数字分别是a3,a2,a1,a0,则这个四位数可以写成
1000a3+100a2+10a1+a0,
它的各位数字之和的10倍是
10(a3+a2+a1+a0)=10a3+10a2+10a1+10a0,
这个四位数与它的各位数字之和的10倍的差是
990a3+90a2-9a0=1998,
110a3+10a2-a0=222。
比较上式等号两边个位、十位和百位,可得
a0=8,a2=1,a3=2。
所以红色卡片上是2,黄色卡片上是1,蓝色卡片上是8。
解:依题意,得
a+b+c>14,
说明:求解本题所用的基本知识是,正整数的十进制表示法和最简单的不定方程。
例3 从自然数1,2,3,…,1000中,最多可取出多少个数使得所取出的数中任意三个数之和能被18整除?
解:设a,b,c,d是所取出的数中的任意4个数,那么
a+b+c=18m,a+b+d=18n,
其中m,n是自然数。于是
c-d=18(m-n)。
上式说明所取出的数中任意2个数之差是18的倍数,即所取出的每个数除以18所得的余数均相同。设这个余数为r,那么
a=18a1+r,b=18b1+r,c=18c1+r,
其中a1,b1,c1是整数。于是
a+b+c=18(a1+b1+c1)+3r。
因为18|(a+b+c),所以18|3r,即6|r,推知r=0,6,12。因为1000=55×18+10,所以,从1,2,…,1000中可取6,24,42,…,996共56个数,它们中的任意3个数之和能被18整除。
例4 求自然数N,使得它能被5和49整除,并且包括1和N在内,它共有10个约数。
解:把数N写成质因数乘积的形式
由于N能被5和72=49整除,故a3≥1,a4≥2,其余的指数ak为自然数或零。依题意,有
(a1+1)(a2+1)…(an+1)=10。
由于a3+1≥2,a4+1≥3,且10=2×5,故
a1+1=a2+1=a5+1=…=an+1=1,
即a1=a2=a5=…an=0,N只能有2个不同的质因数5和7,因为a4+1≥3>2,故由
(a3+1)(a4+1)=10
知,a3+1=5,a4+1=2是不可能的。因而a3+1=2,a4+1=5,即N=52-1×75-1=5×74=12005。
例5 如果N是1,2,3,…,1998,1999,2000的最小公倍数,那么N等于多少个2与1个奇数的积?
解:因为210=1024,211=2048>2000,每一个不大于2000的自然数表示为质因数相乘,其中2的个数不多于10个,而1024=210,所以,N等于10个2与某个奇数的积。
说明:上述5例都是根据题目的自身特点,从选择恰当的整数表示形式入手,使问题迎刃而解。
二、枚举法
枚举法(也称为穷举法)是把讨论的对象分成若干种情况(分类),然后对各种情况逐一讨论,最终解决整个问题。
运用枚举法有时要进行恰当的分类,分类的原则是不重不漏。正确的分类有助于暴露问题的本质,降低问题的难度。数论中最常用的分类方法有按模的余数分类,按奇偶性分类及按数值的大小分类等。
例6 求这样的三位数,它除以11所得的余数等于它的三个数字的平方和。
分析与解:三位数只有900个,可用枚举法解决,枚举时可先估计有关量的范围,以缩小讨论范围,减少计算量。
设这个三位数的百位、十位、个位的数字分别为x,y,z。由于任何数除以11所得余数都不大于10,所以
x2+y2+z2≤10,
从而1≤x≤3,0≤y≤3,0≤z≤3。所求三位数必在以下数中:
100,101,102,103,110,111,112,
120,121,122,130,200,201,202,
211,212,220,221,300,301,310。
不难验证只有100,101两个数符合要求。
例7 将自然数N接写在任意一个自然数的右面(例如,将2接写在35的右面得352),如果得到的新数都能被N整除,那么N称为魔术数。问:小于2000的自然数中有多少个魔术数?
对N为一位数、两位数、三位数、四位数分别讨论。
N|100,所以N=10,20,25,50;
N|1000,所以N=100,125,200,250,500;
(4)当N为四位数时,同理可得N=1000,1250,2000,2500,5000。符合条件的有1000,1250。
综上所述,魔术数的个数为14个。
说明:(1)我们可以证明:k位魔术数一定是10k的约数,反之亦然。
(2)这里将问题分成几种情况去讨论,对每一种情况都增加了一个前提条件,从而降低了问题的难度,使问题容易解决。
例8 有3张扑克牌,牌面数字都在10以内。把这3张牌洗好后,分别发给小明、小亮、小光3人。每个人把自己牌的数字记下后,再重新洗牌、发牌、记数,这样反复几次后,3人各自记录的数字的和顺次为13,15,23。问:这3张牌的数字分别是多少?
解:13+15+23=51,51=3×17。
因为17>13,摸17次是不可能的,所以摸了3次, 3张扑克牌数字之和是17,可能的情况有下面15种:
①1,6,10 ②1,7,9 ③1,8,8
④2,5,10 ⑤2,6,9 ⑥2,7,8
⑦3,4,10 ⑧3,5,9 ⑨3,6,8
⑩3,7,7 (11)4,4,9 (12)4,5,8
(13)4,6,7 (14)5,5,7 (15)5,6,6
只有第⑧种情况可以满足题目要求,即
3+5+5=13;3+3+9=15;5+9+9=23。
这3张牌的数字分别是3,5和9。
例9 写出12个都是合数的连续自然数。
分析一:在寻找质数的过程中,我们可以看出100以内最多可以写出7个连续的合数:90,91,92,93,94,95,96。我们把筛选法继续运用下去,把考查的范围扩大一些就行了。
解法1:用筛选法可以求得在113与127之间共有12个都是合数的连续自然数:
114,115,116,117,118,119,120,
121,122,123,124,125,126。
分析二:如果12个连续自然数中,第1个是2的倍数,第2个是3的倍数,第3个是4的倍数……第12个是13的倍数,那么这12个数就都是合数。
又m+2,m+3,…,m+13是12个连续整数,故只要m是2,3,…,13的公倍数,这12个连续整数就一定都是合数。
解法2:设m为2,3,4,…,13这12个数的最小公倍数。m+2,m+3,m+4,…,m+13分别是2的倍数,3的倍数,4的倍数……13的倍数,因此12个数都是合数。
说明:我们还可以写出
13!+2,13!+3,…,13!+13
(其中n!=1×2×3×…×n)这12个连续合数来。
同样,
(m+1)!+2,(m+1)!+3,…,(m+1)!+m+1是m个连续的合数。








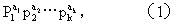
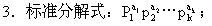


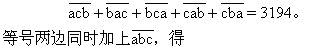
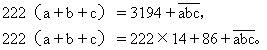

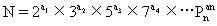
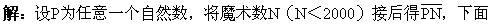
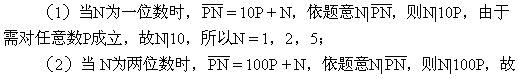
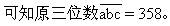














 701
701

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








