高维数值积分数论方法研究开始于20世纪50年代末,其理论基础是数论中的一致分布论。命Us表示 s维单位立方体。假定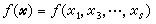
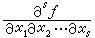

作为Us上定积分
 本文介绍了数论方法在高维数值积分中的应用,特别是科罗博夫-劳卡方法和分圆域方法。这些方法通过选择特定点集来近似积分,并具有与维数无关的误差主阶,适用于高维度问题的计算。科罗博夫-劳卡方法的点集构造存在挑战,而分圆域方法虽然计算量较小但误差稍大。已有相关表提供参考数据。
本文介绍了数论方法在高维数值积分中的应用,特别是科罗博夫-劳卡方法和分圆域方法。这些方法通过选择特定点集来近似积分,并具有与维数无关的误差主阶,适用于高维度问题的计算。科罗博夫-劳卡方法的点集构造存在挑战,而分圆域方法虽然计算量较小但误差稍大。已有相关表提供参考数据。
高维数值积分数论方法研究开始于20世纪50年代末,其理论基础是数论中的一致分布论。命Us表示 s维单位立方体。假定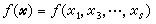
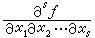

作为Us上定积分
 432
432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


