引用请标明出处:http://blog.csdn.net/callon_h/article/details/51340976
FFT意为快速傅立叶变换,想要捡起FFT自然免不了了解傅立叶变换:
从理解上,请参考
http://daily.zhihu.com/story/3935067
从公式上,由于三角函数集1, coswt, cos2wt, …, cosnwt, …, sinwt, sin2wt, …, sinnwt, …,在区间(t0, t0+T)内是正交函数集,所以任何一个周期函数f(t)都可以由它们的线性组合来表示,即
f(t) = a0/2 + a1*coswt + a2*cos2wt + … + b1*sinwt +b2*sin2wt + …
如果你知道f(t),怎么求a0,a1…b1,b2…这些系数?
例:如果你要求a2,上述等式两边乘以cos2wt:
f(t)cos2wt = a2(cos2wt)^2+a0*cos2wt
两边取(t0, t0+T)的积分,即可得到a2的值,点到为止吧,思想有了就好。
同理,由于e^(jwt)也是正交函数集,所以也能得到类似的结论,和之前也类似地,两边同乘一个e^(-jnwt)就可得到结果,其中n就看你要求哪一项的系数来定了。
了解完傅立叶变换,还需要知道离散傅立叶变换,因为FFT正是为了解决离散傅立叶变换的运算量而产生的:
其实本质只是傅立叶变换的变形,看看公式对比就明白了,
X(k) = x(0)*W^(0*k) + x(1)*W^(1*k) + x(2)*W(2*k)+…
其中,X(k)是变换结果,也是之前的那些系数,x(n)是原始离散采集样本,W=e^(-j*2*PI/N),N=采集到的总点数,PI=3.1415926…
总而言之,只是把积分换成求和罢了。
终于到了正题,快速傅立叶变换到底是什么?
上部分说了,是为了解决离散傅立叶变换的大运算量引进的一种方法,之前的运算量有多大呢?
为了求得一个X(k),需要做N次乘法和N-1次加法,为了求得所有的X(k)就需要做N^2次乘法和N*(N-1)次加法。但是为什么能够减少运算量,原因在于W^nk有周期性和对称性:
W^n(k+N) = W^nk
W^k(n+N) = W^nk
W^(nk+N/2) = -W^nk
通过这些性质,可以避免很多重复运算。把x(n)序列按奇偶分组的蝶形运算,可以降低到(N/2)*log2(N)次乘法和N*log2(N)次加法。
蝶形运算:
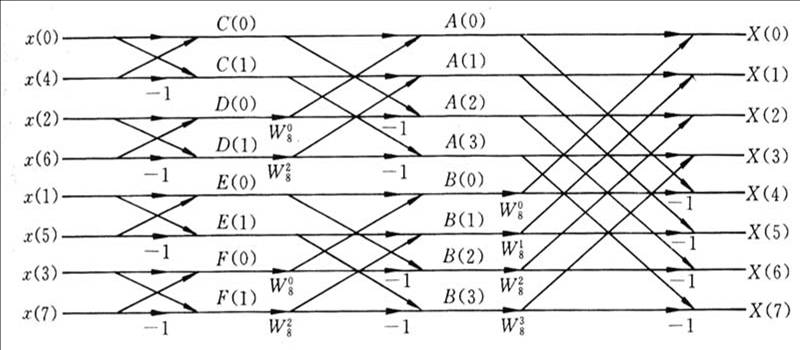
上图为N=8时的蝶形运算流程图,可以发现,只是把W^nk减少了一半(所以这里不用W^nk,而只是W以N为底k为序数,因为之前性质啦),并且对x(n)进行在倒位排序交叉运算而已。
倒位排序的含义(个人理解):
如果N=8,那么第1位倒位序就从001变成了100(4),x(1)和x(4)交换,第2位不变,第3位从011变成了110(6),x(3)和x(6)交换…
如果N=16,那么第1位倒位序从0001变成了1000(8),x(1)和x(8)交换,第2位倒位序从0010变成了0100(4),x(2)和x(4)交换,第3位从0011变成了1100(12),x(3)和x(12)交换…
理解了整个过程,移植为任何语言都不是问题。最后用C语言,一步步来完成fft运算吧,需要注意的是,C语言编写位运算替代除法效率会更高更准确:
参考了
http://www.tuicool.com/articles/FzAJza
因为FFT涉及到了复数运算,C语言中需要定义“复数“这样一个结构体/PI/复数的加法/减法/乘法/除法/取模:
#ifndef __FFT_H__
#define __FFT_H__
typedef struct complex
{
float real;
float imag;
}complex;
#define PI 3.1415926
void conjugate_complex(int n, complex in[], complex out[]);
void c_plus(complex a, complex b, complex *c);
void c_mul(complex a, complex b, complex *c) ;
void c_sub(complex a, complex b, complex *c);
void c_div(complex a, complex b, complex *c);
void c_abs(complex f[], float out[], int n);
#endif简单的函数直接附上代码,最后详细看看FFT的实现就好:
#include "math.h"
#include "fft.h"
///////////////////////////////////////
void conjugate_complex(int n,complex in[],complex out[])
{
int i = 0;
for(i=0;i<n;i++)
{
out[i].imag = -in[i].imag;
out[i].real = in[i].real;
}
}
///////////////////////////////////////
void c_abs(complex f[],float out[],int n)
{
int i = 0;
float t;
for(i=0;i<n;i++)
{
t = f[i].real * f[i].real + f[i].imag * f[i].imag;
out[i] = sqrt(t);
}
}
///////////////////////////////////////
void c_plus(complex a,complex b,complex *c)
{
c->real = a.real + b.real;
c->imag = a.imag + b.imag;
}
///////////////////////////////////////
void c_sub(complex a,complex b,complex *c)
{
c->real = a.real - b.real;
c->imag = a.imag - b.imag;
}
////////////////////////////////////////
void c_mul(complex a,complex b,complex *c)
{
c->real = a.real * b.real - a.imag * b.imag;
c->imag = a.real * b.imag + a.imag * b.real;
}
////////////////////////////////////////
void c_div(complex a,complex b,complex *c)
{
c->real = (a.real * b.real + a.imag * b.imag)/(b.real * b.real +b.imag * b.imag);
c->imag = (a.imag * b.real - a.real * b.imag)/(b.real * b.real +b.imag * b.imag);
}
/////////////////////////////////////////
#define SWAP(a,b) tempr=(a);(a)=(b);(b)=tempr
void Wn_i(int n,int i,complex *Wn)
{
Wn->real = cos(2*PI*i/n);
Wn->imag = -sin(2*PI*i/n);
}void Wn_i(int n,int i,complex *Wn,char flag)这个函数稍微多说一嘴吧,因为蝶形运算图中有W以N(图中为8)为底,k为序数的值,W是e^(-j*2*PI/N),所以这个值是e^(-j*2*PI*k/N),根据欧拉公式写成三角函数式便是cos(2*PI*i/n)-j*sin(2*PI*i/n)。
然后分析蝶形运算过程:
void fft(int N,complex f[])
首先,输入的点数最好是2^M这种形式,需要求得M,再将x(n)进行重新倒位排序,排序成蝶形运算的顺序:
//计算分解的级数M=log2(N)
for(i=N,M=1;(i>>=1)!=1;M++);
//重新排列原信号
for(i=1,j=N>>1;i<=N-2;i++)
{
if(i<j)
{
t=x[j];
x[j]=x[i];
x[i]=t;
}
k=N>>1;
while(k<=j)
{
j=j-k;
k>>=1;
}
j=j+k;
}由之前的图,得到实现的流程和该有的参数:
1.交叉运算的列一共是3列,这个3正好是由8=2^3来决定的,所以蝶形运算最大的循环应该是上面代码求得的M。
2.同一个序数的W,比如W以8为底0为序数的计算相隔,当m=1时,相隔2,m=2时,相隔4,m=3时只出现了一次,可以理解为相隔8,所以规律为2^m,其中m是从1逼向M。
3.x(n)的交叉运算,“叉“的宽度越来越大,分别是1/2/4,2^(m-1)刚好就是1/2/4。
4.W的序数k的规律,m=1全是0,m=2是0和2,m=3是0/1/2/3,规律可以由:(自然数[从1到m]-1)*2^(M-m) 来描述。
从而可以得到蝶形运算的代码(希望读者可以根据上述总结自行编写,以下为个人参考并总结后编写)
for(m=1;m<=M;m++)
{
la=1<<m;
lb=la>>1;
for(l=1;l<=lb;l++)
{
r=(l-1)*(1<<(M-m));
for(n=l-1;n<N;n=n+la)
{
lc=n+lb;
Wn_i(N,r,&wn);
c_mul(x[lc],wn,&t);
c_sub(x[n],t,&(x[lc]));
c_plus(x[n],t,&(x[n]));
}
}
}完整的FFT函数程序:
void callon_fft(int N,complex x[])
{
complex t,wn;
int i,j,k,m,n,l,r,M;
int la,lb,lc;
for(i=N,M=1;(i>>=1)!=1;M++);
for(i=1,j=N>>1;i<=N-2;i++)
{
if(i<j)
{
t=x[j];
x[j]=x[i];
x[i]=t;
}
k=N>>1;
while(k<=j)
{
j=j-k;
k>>=1;
}
j=j+k;
}
for(m=1;m<=M;m++)
{
la=1<<m;
lb=la>>1;
for(l=1;l<=lb;l++)
{
r=(l-1)*(1<<(M-m));
for(n=l-1;n<N;n=n+la)
{
lc=n+lb;
Wn_i(N,r,&wn);
c_mul(x[lc],wn,&t);
c_sub(x[n],t,&(x[lc]));
c_plus(x[n],t,&(x[n]));
}
}
}
}
在MSP430F4250上测试FFT:
#include <msp430x42x0.h>
#include "FFT.h"
#define FFT_NUMBER 8 //16
complex f1[FFT_NUMBER];
void main(void)
{
volatile unsigned int i; // Use volatile to prevent removal
// by compiler optimization
WDTCTL = WDTPW + WDTHOLD; // Stop WDT
FLL_CTL0 |= XCAP14PF+DCOPLUS; // Configure load caps
// SCFQCTL = SCFQ_4M;
SCFI0 |= FN_2;
for (i = 0; i < 10000; i++); // Delay for 32 kHz crystal to
// stabilize
for(i=0;i<FFT_NUMBER;i++)
{
f1[i].real=i;
}
callon_fft(FFT_NUMBER,f1);
while(1);
}
调试打断点得到送进FFT的初始值:

做完FFT之后的结果:
和matlab结果进行对比:
同理获得16点的对比:
但是MSP430F4250只能测试到16,没办法测试更多数据,不过该程序也非常容易放到PC机上运行,如下是Xcode下运行结果:
经PC机测试多次,和matlab下运行无差别,读者可自行测试。
所有知识点为个人理解和总结,所有程序代码为自己参考和理解并完善,仅供参考,如有问题欢迎反馈,共同进步,有帮助欢迎评论点赞。

























 4127
4127











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








