1、信息增益
在学习决策树时接触到到了信息增益(Information Gain),由此了解到熵。不解顺序查之。
在划分数据集之前之后信息发生的变化成为信息增益。因此,在决策树的根节点,选用的判定划分的属性,在划分数据前后信息的变化越大,那该属性对数据集的划分作用越大,分类的效果越好,也就是信息增益越大。所以获得信息增益最高的特征就是选择的最好特征。
举个例子:
我们要建立的决策树的形式类似于“如果天气怎么样,去玩;否则,怎么着怎么着”的树形分叉。那么问题是用哪个属性(即变量,如天气、温度、湿度和风力)最适合充当这颗树的根节点,在它上面没有其他节点,其他的属性都是它的后续节点。借用信息论的概念,我们用一个统计量,“信息增益”(InformationGain)来衡量一个属性区分以上数据样本的能力。信息增益量越大,这个属性作为一棵树的根节点就能使这棵树更简洁,比如说一棵树可以这么读成,如果风力弱,就去玩;风力强,再按天气、温度等分情况讨论,此时用风力作为这棵树的根节点就很有价值。如果说,风力弱,再又天气晴朗,就去玩;如果风力强,再又怎么怎么分情况讨论,这棵树相比就不够简洁了。
所以,信息增益越大,信息对数据的区分能力就越强。
信息增益的公式:
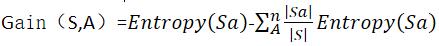
其中,|S|为原集合的数量,|Sa|为分类后子集中元素的个数。Entropy(S)为原集合的熵
所以,G(S,A)是在给定属性A的值知道后,导致期望熵的减少,也就是说,若知道A的值,可以获得最大的信息增益,则属性A对数据集分类数量的降低有很大的积极作用。知道A之后,得到的信息是相对其他属性最多的。
2、熵
计算信息增益需要用到熵,集合信息的度量方式成为香农熵(熵),熵定义为信息的期望值。
符号xi的信息定义:l(xi)=-log2P(xi),其中P(xi)是选择该分类的概率。
熵的计算公式:
吴军在《数学之美系列四–怎样度量信息?》中认为信息熵的大小指的的是了解一件事情所需要付出的信息量是多少,这件事的不确定性越大,要搞清它所需要的信息量也就越大,也就是它的信息熵越大。
Matrix67在《互联网时代的社会语言学:基于SNS的文本数据挖掘》认为信息熵衡量的是在你知道一个事件的结果后平均会给你带来多大的信息量。如果一颗骰子的六个面都是 1 ,投掷它不会给你带来任何新信息,因为你知道它的结果肯定是1,它的信息熵为 - log(1) = 0 。(log是以2为底,lg是以10为底)
两种解释在不同的应用上可以有不同的理解。例如在《文本分类入门(十一)特征选择方法之信息增益》可以看出在文本分类中对信息熵的理解是第二种。不过,两种理解其实都指出了信息熵的另一个作用,就是信息熵可以衡量事物的不确定性,这个事物不确定性越大,信息熵也越大,也可以说事件的无序程度越高。
Q:可不可以理解成一件事情越复杂,信息熵越大。那么从公式上怎么看出,信息熵代表一件事的复杂程度???
A:一个事件的不确定性越大,那么一个事件可能的发生的情况越多,公式中的n越大,结果越大。
PS:关于比特
信息论中,确定了要编码集合S中任意成员的分类所需要的最少二进制位数。
为何信息熵会有这样的作用?为何它的公式这样表示?所以还需要理解信息量这一的概念。香农用“比特”这个概念来度量信息量。也即信息量的多少就是比特的多少。
32只球队共有32种夺冠的可能性,用多少信息量才能包括这32个结果?按照计算机的二进制(只有1和0)表示法,我们知道2^5=32 ,也就是需要5符号的组合结果就可以完全表示这32个变化,而这里的符号通常称之为比特。既然是这样,那么当一件事的结果越不确定时,也就是变化情况越多时,那么你若想涵盖所有结果,所需要的比特就要越多,也就是,你要付出的信息量越大,也即信息熵越大。当然,每个变化出现的概率不同,因而在香农的公式中才会用概率,所以信息熵算的是了解这件事所付出的平均信息量。比如这个例子里假设32只球队夺冠可能性相同,即Pi=1/32 ,那么按照香农公式计算:
entropy(P1,P2,…,P32)=-(1/32)log(1/32)-(1/32)log(1/32)……-(1/32)log(1/32)
=5/32+5/32…+5/32
=(5*32)/32
=5








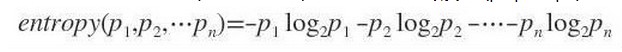

















 3770
3770

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








