平衡二叉搜索树的插入与删除

最新推荐文章于 2024-05-25 20:17:22 发布
最新推荐文章于 2024-05-25 20:17:22 发布
阅读量753 收藏 2
点赞数
分类专栏： 数据结构（严蔚敏版复习）
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/caoleiwe/article/details/106332686
版权

     以下内容主要参考了严蔚敏版的《数据结构》教材，但是教材里面只介绍了插入操作没有介绍删除操作，刚好在这篇文章里面有介绍删除操作且他好像也是参考严蔚敏版的《数据结构》教材里面的内容，因此我的删除操作主要参考于他这篇文章。
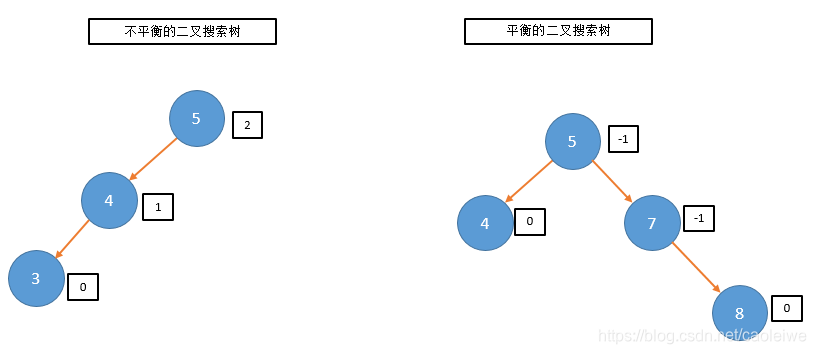
     二叉树中的一个节点的平衡因子为其左子树的高度减去其右子树的高度的值。如果一颗二叉树中所有节点的平衡因子的绝对值都小于2则这颗二叉树是一颗平衡的二叉树，否则该二叉树是不平衡的。在这里我们同时假定这里的二叉树是二叉搜索树。平衡二叉搜索树和不平衡二叉搜索树的例子见图1。

　
图 1.

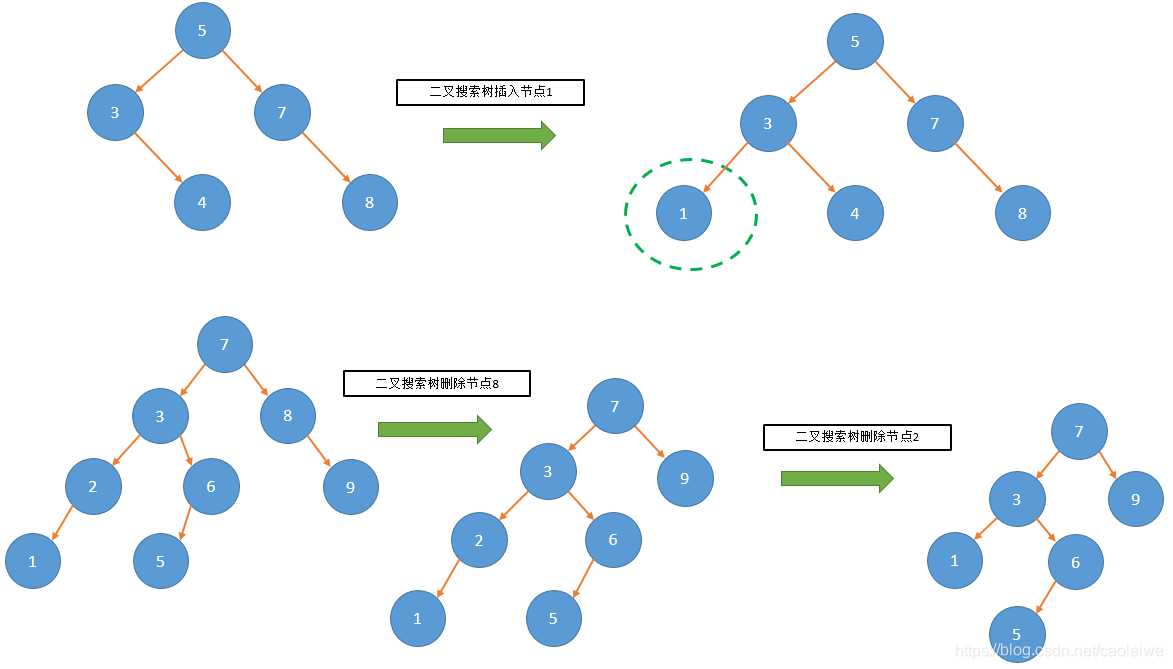
     如果首先不去理会二叉树的平衡性，则插入与删除操作就是二叉搜索树的插入与删除。对于插入操作，首先是在二叉树中查找有没有要插入的元素如果有则返回，不进行任何操作，如果没有则新建一节点并将该节点插入到某个节点（查找待插入元素时遇到的空节点父节点）的左孩子或右孩子。对于删除操作，如果二叉搜索树中不存在待删除的元素，则立即返回不做任何操作。如果待删除的元素在二叉搜索树中只有左子树或只有右子树，则将其左子树或右子树设为待删除的元素父节点的左子树或右子树（这要看待删除元素是其父节点的左孩子还是右孩子）。此种情况的例子见图2。

　
图 2.

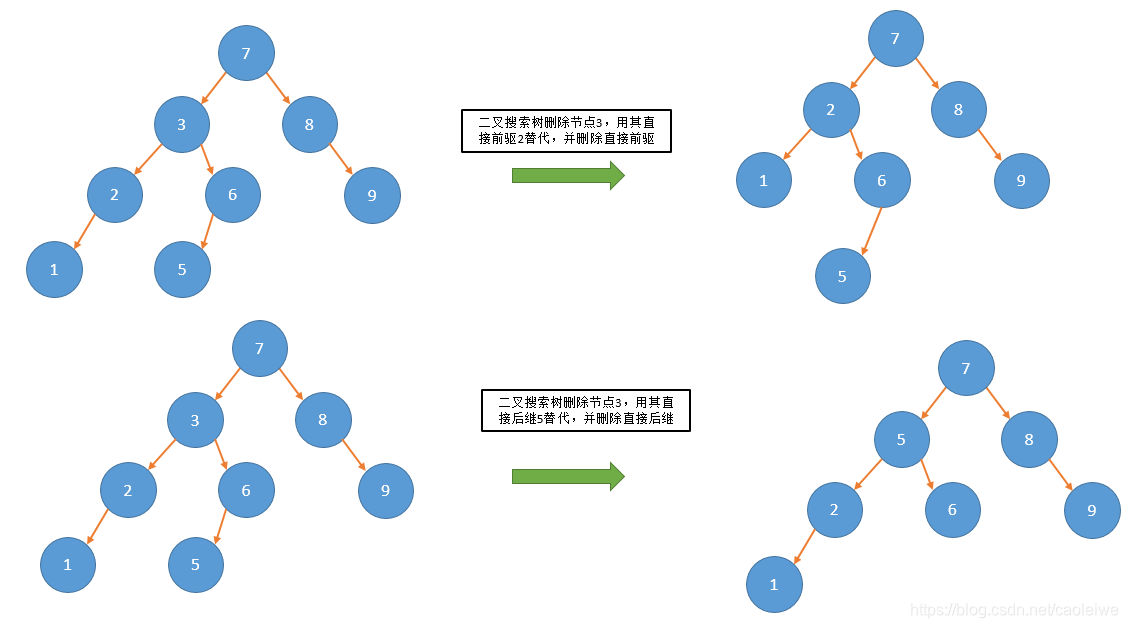
     如果待删除节点既有左孩子又有右孩子，此时可以用在中序遍历中该节点的直接前驱或者直接后继替代该节点。如果是用其直接前驱替代该节点，则该直接前驱必定是该节点左子树中最右的节点，也是其左子树中值最大的节点且其右子树为空。替代完之后删除前驱节点即可，此时转换为删除只有左子树或只有右子树的节点的情况。如果是用其直接后继替代该节点，则该直接后继必定是该节点右子树中最左的节点，也是其左子树中值最小的节点且为叶子节点。替代完之后删除后继节点即可，此时转换为删除叶子节点的情况。此种情况的例子见图3。

　
图 3.

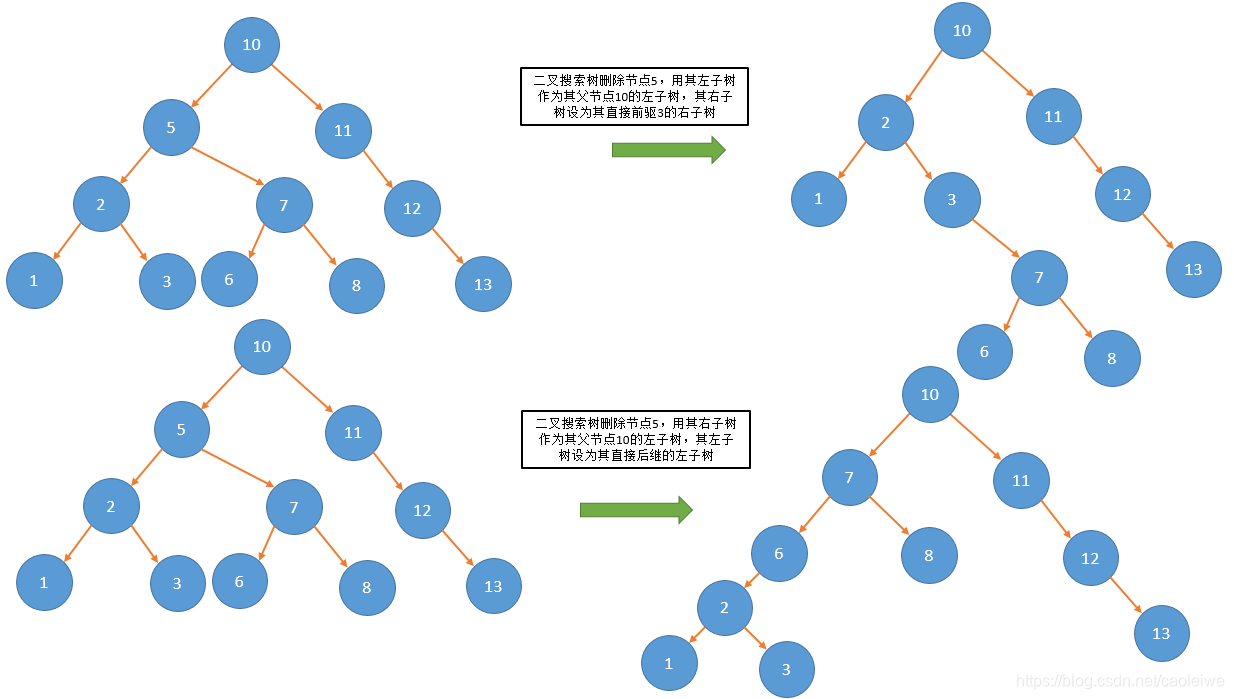
     如果待删除节点既有左孩子又有右孩子。若待删除节点为其父节点的左孩子，节点S为待删除节点在中序遍历序列中的直接前驱（节点S的右孩子为空），则可以将待删除节点的左子树设为其父节点的左子树，将待删除节点的右子树设为节点S的右子树。若待删除节点为其父节点的左孩子，节点S为待删除节点在中序遍历序列中的直接后继（节点S的左孩子为空），则可以将待删除节点的右子树设为其父节点的左子树，将待删除节点的左子树设为节点S的左子树。此种情况的例子见图4。若待删除节点为其父节点的右孩子，节点S为待删除节点在中序遍历序列中的直接后继（节点S的左孩子为空），则可以将待删除节点的右子树设为其父节点的右子树，将待删除节点的左子树设为节点S的左子树。若待删除节点为其父节点的右孩子，节点S为待删除节点在中序遍历序列中的直接前驱（节点S的右孩子为空），则可以将待删除节点的左子树设为其父节点的右子树，将待删除节点的右子树设为节点S的右子树。此种情况的例子见图5。

　
图 4.
　
图 5.

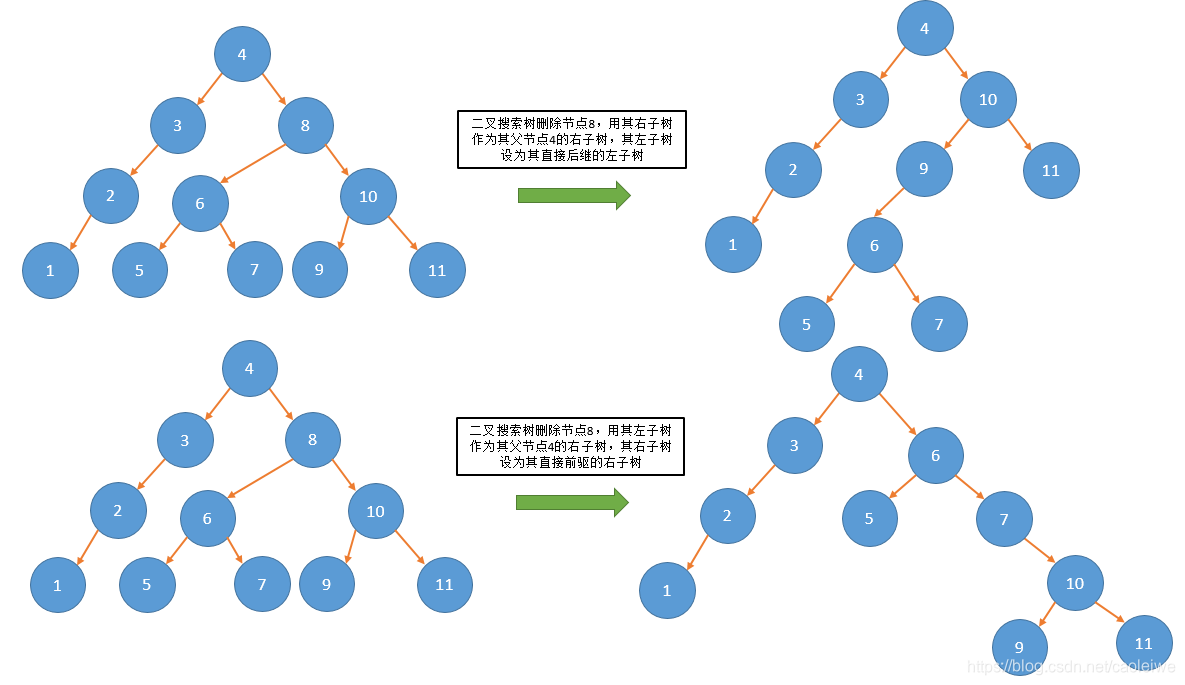
     在以下平衡二叉搜索树删除算法的实现中，如果待删除节点既有左孩子又有右孩子，我们用在中序遍历中该节点的直接前驱替代该节点。
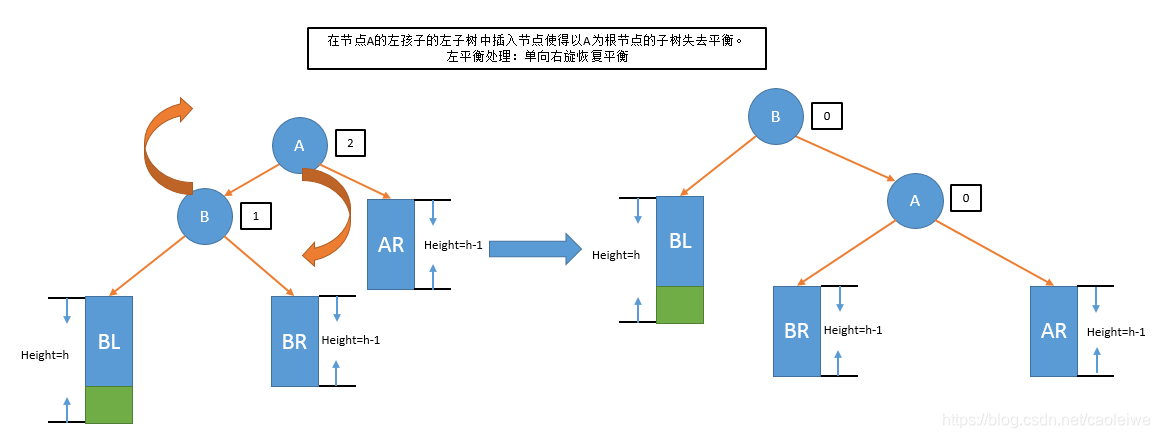
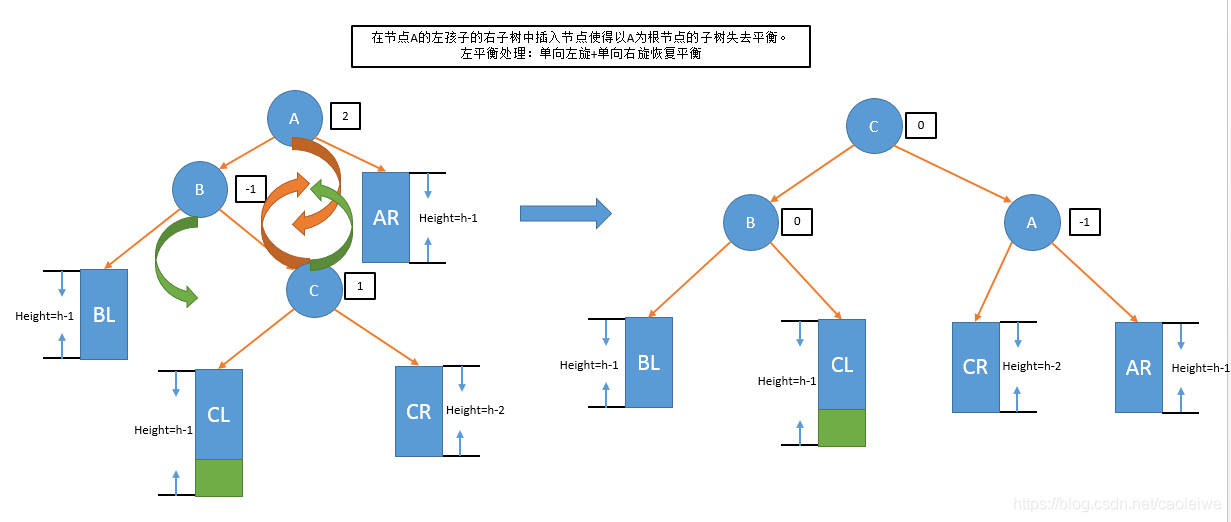
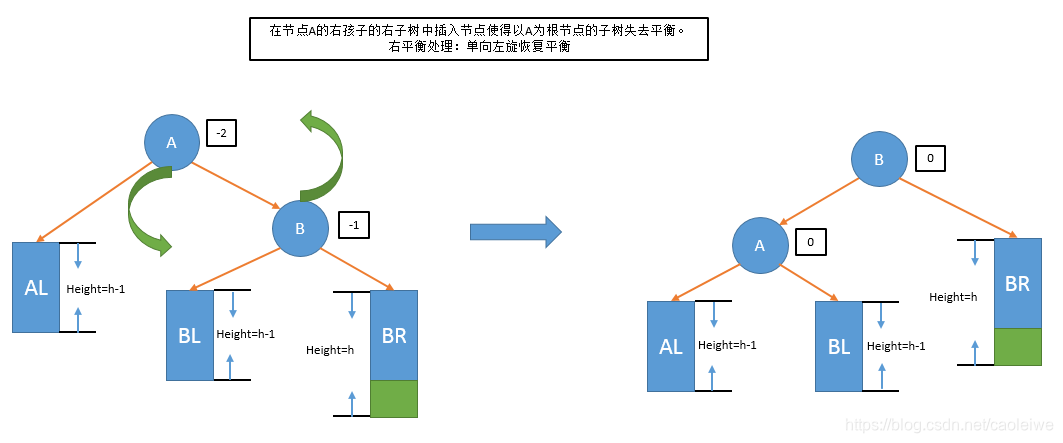
     在平衡二叉搜索树中插入或删除节点后，如果没有改变平衡性则不必理会。如果出现不平衡的情况则必须进行调整使得其恢复平衡特性。假设由于在平衡二叉搜索树中插入节点D而失去平衡的最小子树根节点为A（即离插入节点D最近且平衡因子绝对值超过1的祖先节点），则失去平衡后进行调整的规律可以归纳为以下四种情况，分别如图6、7、8、9所示：

  • 左平衡处理：单向右旋恢复平衡（在节点A的左孩子的左子树中插入节点使得以A为根节点的子树失去平衡）
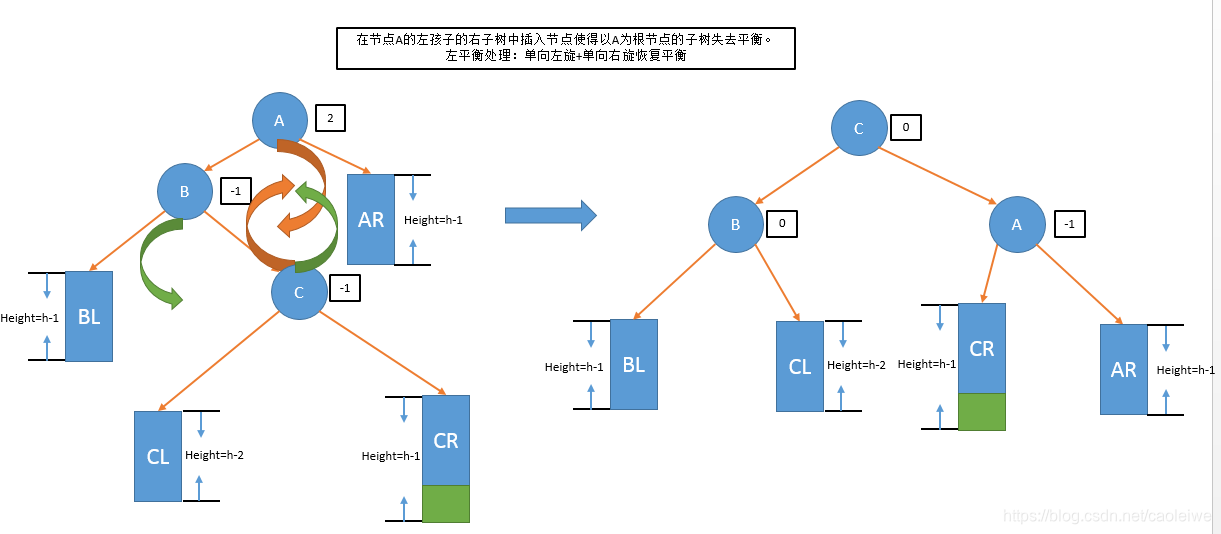
  • 左平衡处理：单向左旋+单向右旋恢复平衡（在节点A的左孩子的右子树中插入节点使得以A为根节点的子树失去平衡）
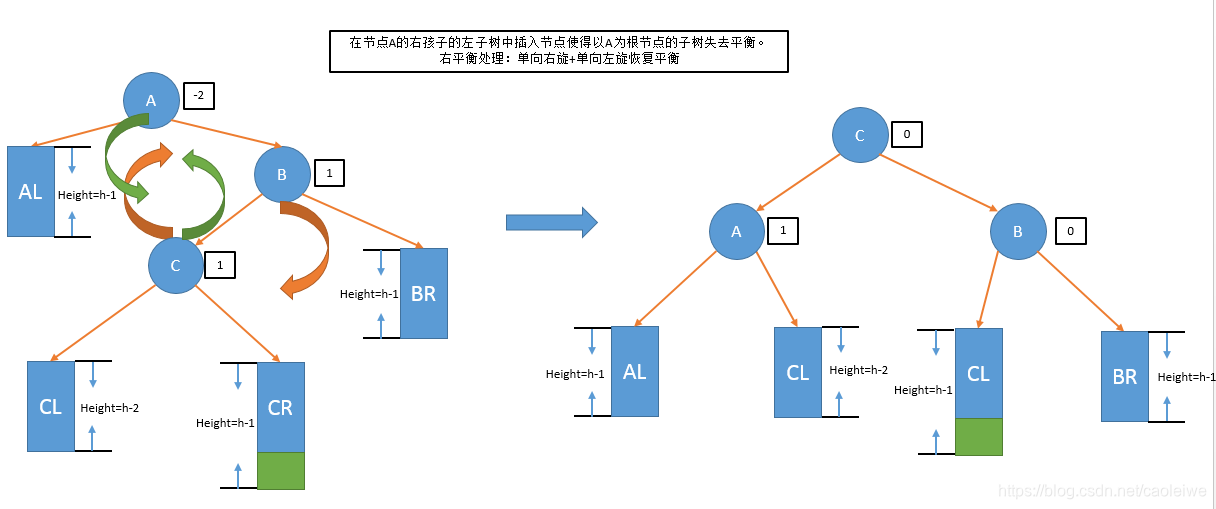
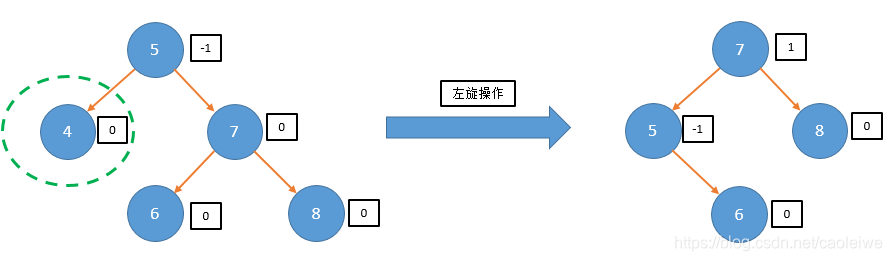
  • 右平衡处理：单向左旋恢复平衡（在节点A的右孩子的右子树中插入节点使得以A为根节点的子树失去平衡）
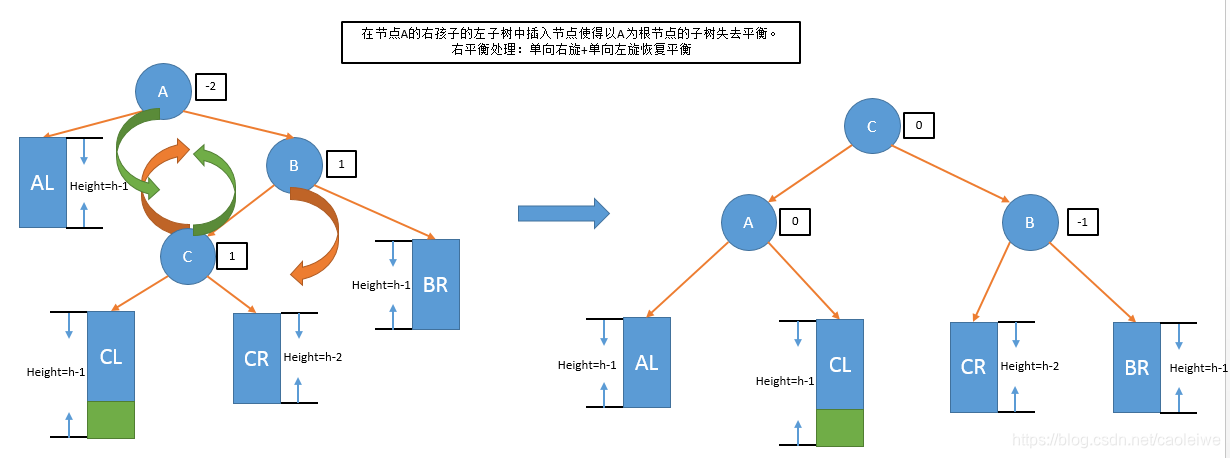
  • 右平衡处理：单向右旋+单向左旋恢复平衡（在节点A的右孩子的左子树中插入节点使得以A为根节点的子树失去平衡）
　
图 6.
　
图 7.
　
图 8.
　
图 9.

     从以上操作可以看出一共有两种平衡处理（左平衡处理：在节点A的左子树中插入节点使得树不在平衡，右平衡处理：在节点A的右子树中插入节点使得树不再平衡，）以及两种旋转操作（左旋以及右旋）。两种平衡处理分别对应函数 B i n a r y S e a r c h N o d e ∗ l e f t B a l a n c e ( B i n a r y S e a r c h N o d e ∗ r o o t , B i n a r y S e a r c h N o d e ∗ f a t h e r ) BinarySearchNode* leftBalance(BinarySearchNode* root, BinarySearchNode* father) BinarySearchNode∗leftBalance(BinarySearchNode∗root,BinarySearchNode∗father)和 B i n a r y S e a r c h N o d e ∗ r i g h t B a l a n c e ( B i n a r y S e a r c h N o d e ∗ r o o t , B i n a r y S e a r c h N o d e ∗ f a t h e r ) BinarySearchNode* rightBalance(BinarySearchNode * root, BinarySearchNode * father) BinarySearchNode∗rightBalance(BinarySearchNode∗root,BinarySearchNode∗father),两种旋转操作分别对应函数 B i n a r y S e a r c h N o d e ∗ R _ R o t a t e ( B i n a r y S e a r c h N o d e ∗ r o o t , B i n a r y S e a r c h N o d e ∗ f a t h e r ) BinarySearchNode* R\_Rotate(BinarySearchNode* root, BinarySearchNode* father) BinarySearchNode∗R_Rotate(BinarySearchNode∗root,BinarySearchNode∗father)和 B i n a r y S e a r c h N o d e ∗ L _ R o t a t e ( B i n a r y S e a r c h N o d e ∗ r o o t , B i n a r y S e a r c h N o d e ∗ f a t h e r ) BinarySearchNode* L\_Rotate(BinarySearchNode* root, BinarySearchNode* father) BinarySearchNode∗L_Rotate(BinarySearchNode∗root,BinarySearchNode∗father)。对于具体的实现请看源码解释。

　
图 10.
　
图 11.
　
图 12.
　
图 13.
　
图 14.
　
图 15. 
class BinarySearchNode
{
private:
	int data;
	int balanceFactor;
	BinarySearchNode* left;
	BinarySearchNode* right;
public:
	BinarySearchNode(int d1 = 0, int d2 = 0)
	{
		data = d1;
		balanceFactor = d2;//平衡因子：左子树的高度减去右子树的高度，如果该值为0、1或-1则以该节点为根的子树是平衡的否则是不平衡的。
		left = nullptr;
		right = nullptr;
	}
	BinarySearchNode* getLeft()
	{
		return left;
	}
	BinarySearchNode* getRight()
	{
		return right;
	}
	void setLeft(BinarySearchNode* value)
	{
		left = value;
	}
	void setRight(BinarySearchNode* value)
	{
		right = value;
	}
	int getData()
	{
		return data;
	}
	void setData(int value)
	{
		data = value;
	}
	int getBalanceFactor()
	{
		return balanceFactor;
	}
	void setBalanceFactor(int value)
	{
		balanceFactor = value;
	}
};

void printBST(BinarySearchNode* root);

//右旋操作
//root可以考虑以上介绍的节点A，father为节点A的父节点
BinarySearchNode* R_Rotate(BinarySearchNode* root, BinarySearchNode* father)
{
	BinarySearchNode* left = root->getLeft();
	root->setLeft(left->getRight());
	left->setRight(root);
	if (father != nullptr)
	{
		if (left->getData() <= father->getData())
		{
			father->setLeft(left);
		}
		else
		{
			father->setRight(left);
		}
		return nullptr;
	}
	else
	{
		return left;
	}
}

//左旋操作
//root可以考虑以上介绍的节点A，father为节点A的父节点
BinarySearchNode* L_Rotate(BinarySearchNode* root, BinarySearchNode* father)
{
	BinarySearchNode* right = root->getRight();
	root->setRight(right->getLeft());
	right->setLeft(root);
	if (father != nullptr)
	{
		if (right->getData() <= father->getData())
		{
			father->setLeft(right);
		}
		else
		{
			father->setRight(right);
		}
		return nullptr;
	}
	else
	{
		return right;
	}
}

void printBST(BinarySearchNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	else
	{
		cout << "data=" << root->getData() << endl;
		cout << "balanceFactor=" << root->getBalanceFactor() << endl;
	}
	printBST(root->getLeft());
	printBST(root->getRight());
}

//左平衡处理
//root可以考虑以上介绍的节点A，father为节点A的父节点
BinarySearchNode* leftBalance(BinarySearchNode* root, BinarySearchNode* father)
{
	BinarySearchNode* left = root->getLeft();
	BinarySearchNode* right = left->getRight();
	BinarySearchNode* newRoot = nullptr;
	switch (left->getBalanceFactor())
	{
	case 1://对应图6的情况
		root->setBalanceFactor(0);
		left->setBalanceFactor(0);
		newRoot = R_Rotate(root, father);
		break;
	case -1:
		switch (right->getBalanceFactor())
		{
		case 1://对应图7的情况
			root->setBalanceFactor(-1);
			left->setBalanceFactor(0);
			break;
		case 0://对应图10的情况
			root->setBalanceFactor(0);
			left->setBalanceFactor(0);
			break;
		case -1://对应图11的情况
			root->setBalanceFactor(0);
			left->setBalanceFactor(1);
			break;
		}
		right->setBalanceFactor(0);
		L_Rotate(root->getLeft(), root);
		newRoot = R_Rotate(root, father);
		break;
	case 0:	  //这种情况只在删除平衡二叉搜索树中的节点的情况下出现，不会在往平衡二叉搜索树中插入节点的情况下出现，并且在其中的旋转操作之后树的高度不变//对应图14的情况
		left->setBalanceFactor(-1);
		root->setBalanceFactor(1);
		newRoot = R_Rotate(root, father);
		break;
	}
	return newRoot;
}

//右平衡处理
//root可以考虑以上介绍的节点A，father为节点A的父节点
BinarySearchNode* rightBalance(BinarySearchNode * root, BinarySearchNode * father)
{
	BinarySearchNode* right = root->getRight();
	BinarySearchNode* left = right->getLeft();
	BinarySearchNode* newRoot = nullptr;
	switch (right->getBalanceFactor())
	{
	case -1://对应图8的情况
		root->setBalanceFactor(0);
		right->setBalanceFactor(0);
		newRoot = L_Rotate(root, father);
		break;
	case 1:
		switch (left->getBalanceFactor())
		{
		case 1://对应图9的情况
			root->setBalanceFactor(0);
			right->setBalanceFactor(-1);
			break;
		case 0://对应图12的情况
			root->setBalanceFactor(0);
			right->setBalanceFactor(0);
			break;
		case -1://对应图13的情况
			root->setBalanceFactor(1);
			right->setBalanceFactor(0);
			break;
		}
		right->setBalanceFactor(0);
		R_Rotate(root->getRight(), root);
		newRoot = L_Rotate(root, father);
		break;
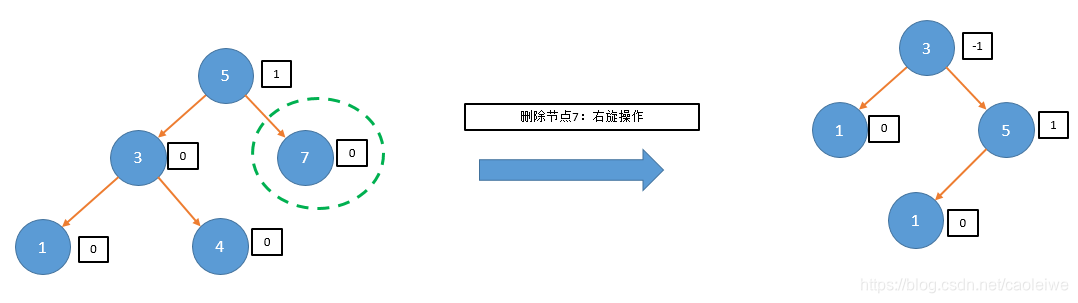
	case 0:	  这种情况只在删除平衡二叉搜索树中的节点的情况下出现，不会在往平衡二叉搜索树中插入节点的情况下出现，并且在其中的旋转操作之后树的高度不变。具体可见example1
		right->setBalanceFactor(1);
		root->setBalanceFactor(-1);
		newRoot = L_Rotate(root, father);
		break;
	}
	return newRoot;
}

//平衡二叉搜索树的插入函数
//参数root为待插入的平衡二叉搜索树的根节点,参数father为待插入的平衡二叉搜索树的根节点的父节点（在首次调用时其为空指针）,参数insertElement为待插入的元素,参数taller用来记录此次插入操作以root为根节点的树个高度是否增高, 如果在插入节点之后树的跟节点变为其它节点则参数newRoot记录新的树根。
int InsertAVL(BinarySearchNode * root, BinarySearchNode * father, int insertElement, bool& taller, BinarySearchNode * &newRoot)
{
	if (root == nullptr) //如果为空则说明找到了插入位置并插入新的节点，参数taller设为true。
	{
		root = new BinarySearchNode(insertElement);
		if (father != nullptr)
		{
			if (insertElement <= father->getData())
			{
				father->setLeft(root);
			}
			else
			{
				father->setRight(root);
			}
			newRoot = nullptr;
			taller = true;
		}
		else
		{
		   //如果father参数为空，则新插入的节点即为根节点
			taller = true;
			newRoot = root;
		}
	}
	else
	{
		if (root->getData() == insertElement)
		{
		   //如果在树中找到了同样的元素则返回什么都不做，return 0;表示没有插入元素。return 1;表示插入了元素。
			taller = false;
			newRoot = nullptr;
			return 0;
		}
		else if (insertElement < root->getData())
		{
		    //如果待插入元素小于当前节点的元素值则递归在左子树上插入
			if (!InsertAVL(root->getLeft(), root, insertElement, taller, newRoot))
			{
				return 0;
			}
			if (taller)
			{
			    //如果在左子树上插入一个节点并且左子树高度增加1
				switch (root->getBalanceFactor())
				{
				case 1://如果当前根节点的平衡因子为1，则当前根节点的平衡因子为现在变为2需要进行左平衡处理。
					newRoot = leftBalance(root, father);
					taller = false;
					break;
				case 0://如果当前根节点的平衡因子为0，则当前根节点的平衡因子为现在变为1，则以当前根节点为根节点的子树高度增加。
					root->setBalanceFactor(1);
					taller = true;
					break;
				case -1://如果当前根节点的平衡因子为-1，则当前根节点的平衡因子为现在变为0，则以当前根节点为根节点的子树高度没有增加。
					root->setBalanceFactor(0);
					taller = false;
					break;
				}
			}
		}
		else if (insertElement > root->getData())
		{
		    //如果待插入元素大于当前节点的元素值则递归在右子树上插入
			if (!InsertAVL(root->getRight(), root, insertElement, taller, newRoot))
			{
				return 0;
			}
			if (taller)
			{
			   //如果在右子树上插入一个节点并且左子树高度增加1
				switch (root->getBalanceFactor())
				{
				case 1://如果当前根节点的平衡因子为1，则当前根节点的平衡因子为现在变为0，则以当前根节点为根节点的子树高度没有增加。
					root->setBalanceFactor(0);
					taller = false;
					break;
				case 0://如果当前根节点的平衡因子为0，则当前根节点的平衡因子为现在变为-1，则以当前根节点为根节点的子树高度增加。
					root->setBalanceFactor(-1);
					taller = true;
					break;
				case -1://如果当前根节点的平衡因子为-1，则当前根节点的平衡因子为现在变为-2需要进行右平衡处理。
					newRoot = rightBalance(root, father);
					taller = false;
					break;
				}
			}
		}
	}
	return 1;
}

//平衡二叉搜索树的删除函数
//参数root为待删除的平衡二叉搜索树的根节点,参数father为待删除的平衡二叉搜索树的根节点的父节点（在首次调用时其为空指针）,参数deleteElement为待删除的元素,参数shorter用来记录此次删除操作以root为根节点的树个高度是否降低, 如果在删除节点之后树的根节点变为其它节点则参数newRoot记录新的树根。
int DeleteAVL(BinarySearchNode * root, BinarySearchNode * father, int deleteElement, bool& shorter, BinarySearchNode * &newRoot)
{
	if (root == nullptr)
	{
	//树为空树，没有任何操作
		shorter = false;
		newRoot = nullptr;
		return 0;
	}
	else
	{
		if (root->getData() == deleteElement)
		{
		   //如果找到待删除节点
			if (root->getLeft() == nullptr)
			{
			//如果待删除节点的左子树为空
				if (father != nullptr)
				{
					if (deleteElement <= father->getData())
					{
						father->setLeft(root->getRight());
						free(root);
					}
					else
					{
						father->setRight(root->getRight());
						free(root);
					}
					newRoot = nullptr;
				}
				else
				{
					newRoot = root->getRight();
					free(root);
				}
				shorter = true;
			}
			else if (root->getRight() == nullptr)
			{
			//如果待删除节点的右子树为空
				if (father != nullptr)
				{
					if (deleteElement <= father->getData())
					{
						father->setLeft(root->getLeft());
						free(root);
					}
					else
					{
						father->setRight(root->getLeft());
						free(root);
					}
					newRoot = nullptr;
				}
				else
				{
					newRoot = root->getLeft();
					free(root);
				}
				shorter = true;
			}
			else
			{
			//如果待删除节点的左右子树均不为空
				BinarySearchNode* q = root;
				BinarySearchNode* s = root->getLeft();
				//找到待删除节点的直接前驱节点
				while (s->getRight() != nullptr)
				{
					q = s;
					s = s->getRight();
				}
				root->setData(s->getData());
				/
				//注意这里不要直接使用下面这段代码来执行删除操作，因为此时待删除节点的左右子树均不为空。如果直接使用下面这段代码执行删除操作的话会造成待删除节点的直接前驱节点到待删除节点之间的节点的平衡因子没有更新，在某些情况下操作完之后树是平衡的，但是某些节点的平衡因子是错的，这样会导致下次删除或插入操作的错误。
				//if (q != root)
				//{
				//	q->setRight(s->getLeft());
				//}
				//else
				//{
				//	q->setLeft(s->getLeft());
				//}
				//free(s);
				/
				//所以这里用待删除节点的直接前驱替代待删除节点之后，相当于在待删除节点的左子树中递归删除以前待删除节点的直接前驱节点。
				if (!DeleteAVL(root->getLeft(), root, s->getData(), shorter, newRoot))
				{
					return 0;
				}
				if (shorter)
				{
					switch (root->getBalanceFactor())
					{
					case 1:
						root->setBalanceFactor(0);
						shorter = true;
						break;
					case 0:
						root->setBalanceFactor(-1);
						shorter = false;
						break;
					case -1:
						if (root->getRight()->getBalanceFactor() == 0)
							shorter = false;
						else
							shorter = true;
						newRoot = rightBalance(root, father);
						break;
					}
				}			
		        
			}
		}
		else if (deleteElement < root->getData())
		{
		  //如果待删除元素小于当前节点元素的值则递归的在其左子树中删除
			if (!DeleteAVL(root->getLeft(), root, deleteElement, shorter, newRoot))
			{
				return 0;
			}
			//如果在左子树上删除一个节点并且左子树高度减1
			if (shorter)
			{
				switch (root->getBalanceFactor())
				{
				case 1:
				//如果当前根节点的平衡因子为1，则当前根节点的平衡因子为现在变为0，则以当前根节点为根节点的子树高度减1。
					root->setBalanceFactor(0);
					shorter = true;
					break;
				case 0:
				//如果当前根节点的平衡因子为0，则当前根节点的平衡因子为现在变为-1，则以当前根节点为根节点的子树高度不变。
					root->setBalanceFactor(-1);
					shorter = false;
					break;
				case -1:
				//如果当前根节点的平衡因子为-1，则当前根节点的平衡因子为现在变为-2，需要进行右平衡处理。
					if (root->getRight()->getBalanceFactor() == 0)
						shorter = false;//对example1的情况
					else
						shorter = true;//对example2的情况
					newRoot = rightBalance(root, father);
					break;
				}
			}
		}
		else if (deleteElement > root->getData())
		{
		   //如果待删除元素大于当前节点元素的值则递归的在其右子树中删除
			if (!DeleteAVL(root->getRight(), root, deleteElement, shorter, newRoot))
			{
				return 0;
			}
			if (shorter)
			{
			//如果在右子树上删除一个节点并且左子树高度减1
				switch (root->getBalanceFactor())
				{
				case 1:
			     //如果当前根节点的平衡因子为1，则当前根节点的平衡因子为现在变为2，需要进行左平衡处理。
					if (root->getLeft()->getBalanceFactor() == 0)
						shorter = false;//对应图14的情况
					else
						shorter = true;//对应图15的情况
					newRoot = leftBalance(root, father);
					break;
				case 0:
			//如果当前根节点的平衡因子为0，则当前根节点的平衡因子为现在变为1，则以当前根节点为根节点的子树高度不变。
					root->setBalanceFactor(1);
					shorter = false;
					break;
				case -1:
				//如果当前根节点的平衡因子为-1，则当前根节点的平衡因子为现在变为0，则以当前根节点为根节点的子树高度减1。
					root->setBalanceFactor(0);
					shorter = true;
					break;
				}
			}
		}
	}
	return 1;
}

     下面放几个简单的例子测试一下插入和删除操作。

　
example1.
　
example2.
　
example3.
　
example4.
　
example5.
　
example6.
　
example7.
　
example8. 
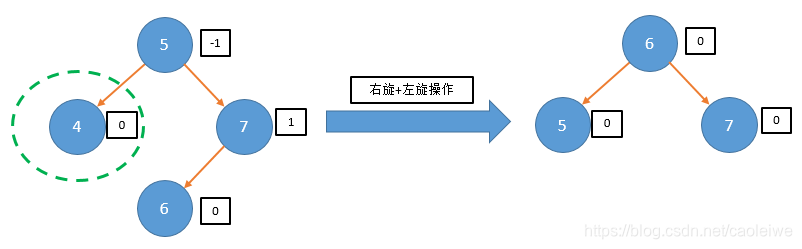
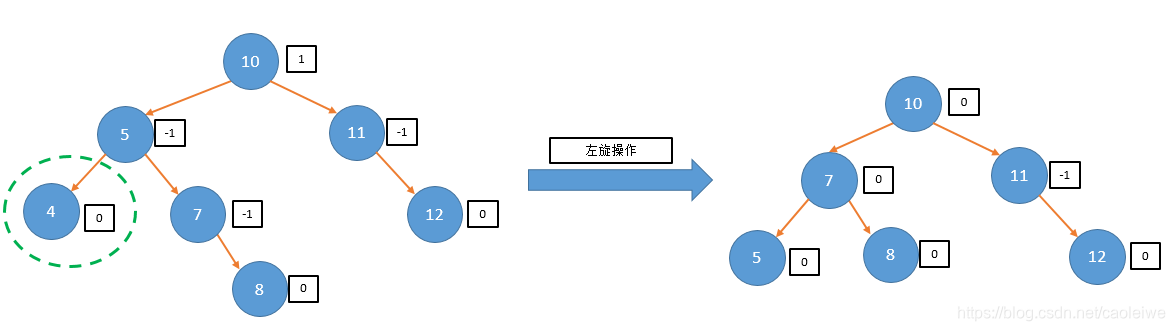
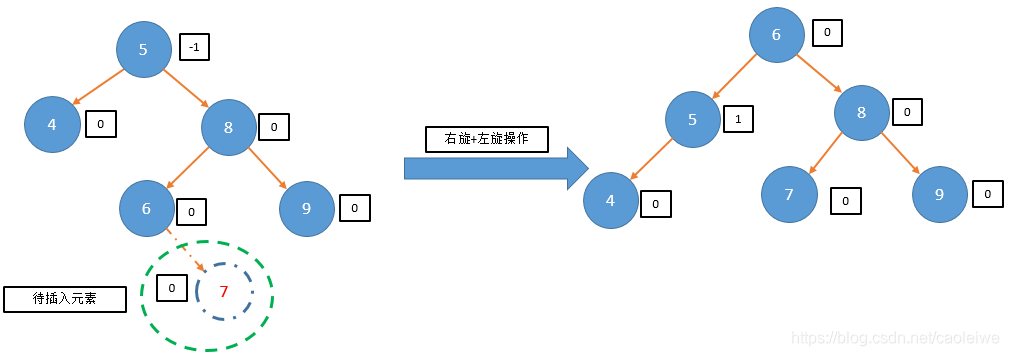
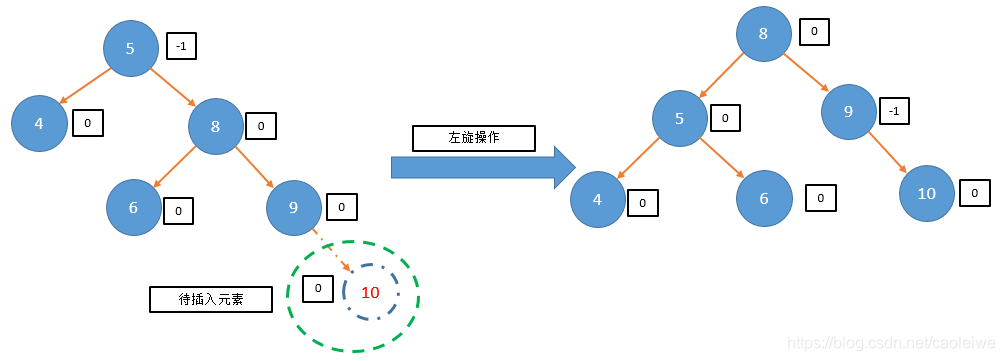
//测试程序
int main()
{
	int status = 0;
	cout << "===================example1==============================" << endl;
	bool shorter1 = false;
	BinarySearchNode* newRoot1 = nullptr;
	BinarySearchNode* root1 = new BinarySearchNode(5,-1);
	BinarySearchNode* root1OfNode4 = new BinarySearchNode(4, 0);
	BinarySearchNode* root1OfNode7 = new BinarySearchNode(7, 0);
	BinarySearchNode* root1OfNode6 = new BinarySearchNode(6, 0);
	BinarySearchNode* root1OfNode8 = new BinarySearchNode(8, 0);
	root1->setLeft(root1OfNode4);
	root1->setRight(root1OfNode7);
	root1OfNode7->setLeft(root1OfNode6);
	root1OfNode7->setRight(root1OfNode8);
	cout << "Original tree is:" << endl;
	printBST(root1);
	status = DeleteAVL(root1,nullptr,4,shorter1,newRoot1);
	cout << "Return status=" << status << endl;
	cout << "The tree after deletion operation is:" << endl;
	if (newRoot1 != nullptr)
	{
		printBST(newRoot1);
	}
	else
	{
		printBST(root1);
	}
	cout << "===================example2==============================" << endl;

	bool shorter2 = false;
	BinarySearchNode* newRoot2 = nullptr;
	BinarySearchNode* root2 = new BinarySearchNode(5, -1);
	BinarySearchNode * root2OfNode4 = new BinarySearchNode(4, 0);
	BinarySearchNode * root2OfNode7 = new BinarySearchNode(7, 1);
	BinarySearchNode * root2OfNode6 = new BinarySearchNode(6, 0);
	root2->setLeft(root2OfNode4);
	root2->setRight(root2OfNode7);
	root2OfNode7->setLeft(root2OfNode6);
	cout << "Original tree is:" << endl;
	printBST(root2);
	status = DeleteAVL(root2, nullptr, 4, shorter2, newRoot2);
	cout << "Return status=" << status << endl;
	cout << "The tree after deletion operation is:" << endl;
	if (newRoot2 != nullptr)
	{
		printBST(newRoot2);
	}
	else
	{
		printBST(root2);
	}

	cout << "===================example3==============================" << endl;
	bool shorter3 = false;
	BinarySearchNode* newRoot3 = nullptr;
	BinarySearchNode* root3 = new BinarySearchNode(10, 1);
	BinarySearchNode* root3OfNode11 = new BinarySearchNode(11, -1);
	BinarySearchNode* root3OfNode12 = new BinarySearchNode(12, 0);
	BinarySearchNode* root3OfNode5 = new BinarySearchNode(5, -1);
	BinarySearchNode * root3OfNode4 = new BinarySearchNode(4, 0);
	BinarySearchNode * root3OfNode7 = new BinarySearchNode(7, -1);
	BinarySearchNode * root3OfNode8 = new BinarySearchNode(8, 0);
	root3->setLeft(root3OfNode5);
	root3->setRight(root3OfNode11);
	root3OfNode5->setLeft(root3OfNode4);
	root3OfNode5->setRight(root3OfNode7);
	root3OfNode7->setRight(root3OfNode8);
	root3OfNode11->setRight(root3OfNode12);
	cout << "Original tree is:" << endl;
	printBST(root3);
	status = DeleteAVL(root3, nullptr, 4, shorter3, newRoot3);
	cout << "The tree after deletion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newRoot3 != nullptr)
	{
		printBST(newRoot3);
	}
	else
	{
		printBST(root3);
	}
	cout << "===================example4==============================" << endl;
	bool taller1 = false;
	BinarySearchNode* newRoot4 = nullptr;
	BinarySearchNode* root4 = new BinarySearchNode(5, -1);
	BinarySearchNode * root4OfNode4 = new BinarySearchNode(4, 0);
	BinarySearchNode * root4OfNode9 = new BinarySearchNode(9, 0);
	BinarySearchNode * root4OfNode6 = new BinarySearchNode(6, 0);
	BinarySearchNode * root4OfNode8 = new BinarySearchNode(8, 0);
	root4->setLeft(root4OfNode4);
	root4->setRight(root4OfNode8);
	root4OfNode8->setLeft(root4OfNode6);
	root4OfNode8->setRight(root4OfNode9);
	cout << "Original tree is:" << endl;
	printBST(root4);
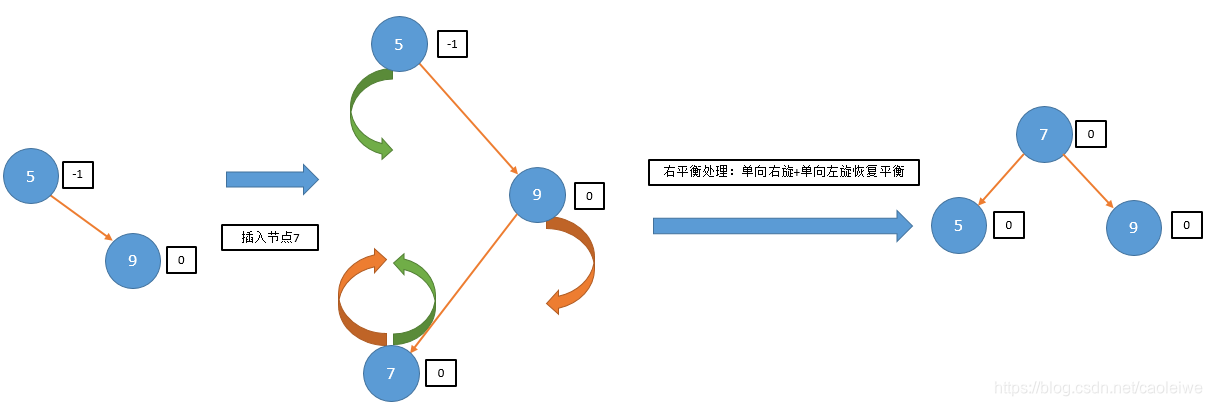
	status = InsertAVL(root4, nullptr, 7, taller1, newRoot4);
	cout << "The tree after insertion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newRoot4 != nullptr)
	{
		printBST(newRoot4);
	}
	else
	{
		printBST(root4);
	}
	cout << "===================example5==============================" << endl;
	bool taller2 = false;
	BinarySearchNode* newroot5 = nullptr;
	BinarySearchNode* root5 = new BinarySearchNode(5, -1);
	BinarySearchNode * root5OfNode4 = new BinarySearchNode(4, 0);
	BinarySearchNode * root5OfNode9 = new BinarySearchNode(9, 0);
	BinarySearchNode * root5OfNode6 = new BinarySearchNode(6, 0);
	BinarySearchNode * root5OfNode8 = new BinarySearchNode(8, 0);
	root5->setLeft(root5OfNode4);
	root5->setRight(root5OfNode8);
	root5OfNode8->setLeft(root5OfNode6);
	root5OfNode8->setRight(root5OfNode9);
	cout << "Original tree is:" << endl;
	printBST(root5);
	status = InsertAVL(root5, nullptr, 10, taller2, newroot5);
	cout << "The tree after insertion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newroot5 != nullptr)
	{
		printBST(newroot5);
	}
	else
	{
		printBST(root5);
	}
	cout << "===================example6==============================" << endl;
	bool taller3 = false;
	BinarySearchNode* newroot6 = nullptr;
	BinarySearchNode* root6 = new BinarySearchNode(6, 1);
	BinarySearchNode* root6OfNode3 = new BinarySearchNode(3, 0);
	BinarySearchNode* root6OfNode7 = new BinarySearchNode(7, 0);
	BinarySearchNode* root6OfNode2 = new BinarySearchNode(2, 0);
	BinarySearchNode* root6OfNode4 = new BinarySearchNode(4, 0);
	root6->setLeft(root6OfNode3);
	root6->setRight(root6OfNode7);
	root6OfNode3->setLeft(root6OfNode2);
	root6OfNode3->setRight(root6OfNode4);
	cout << "Original tree is:" << endl;
	printBST(root6);
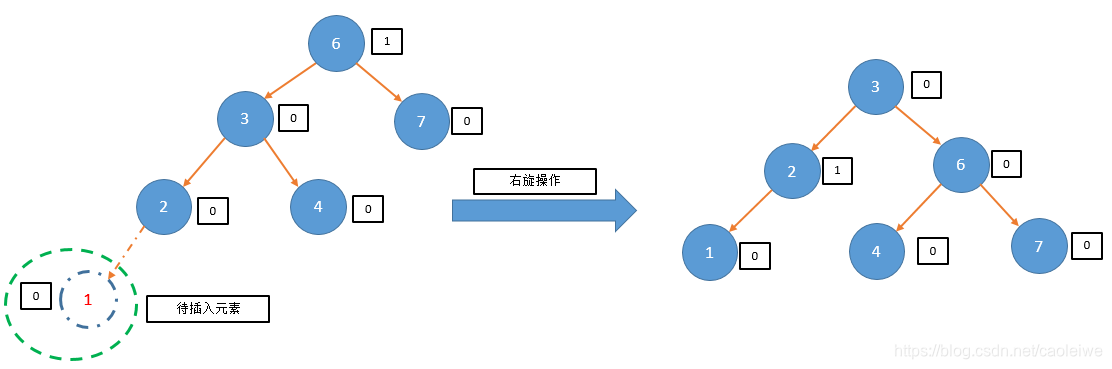
	status = InsertAVL(root6, nullptr, 1, taller3, newroot6);
	cout << "The tree after insertion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newroot6 != nullptr)
	{
		printBST(newroot6);
	}
	else
	{
		printBST(root6);
	}
	cout << "===================example7==============================" << endl;
	bool taller4 = false;
	BinarySearchNode* newroot7 = nullptr;
	BinarySearchNode* root7 = new BinarySearchNode(6, 1);
	BinarySearchNode* root7OfNode3 = new BinarySearchNode(3, 0);
	BinarySearchNode* root7OfNode7 = new BinarySearchNode(7, 0);
	BinarySearchNode* root7OfNode2 = new BinarySearchNode(2, 0);
	BinarySearchNode* root7OfNode4 = new BinarySearchNode(4, 0);
	root7->setLeft(root7OfNode3);
	root7->setRight(root7OfNode7);
	root7OfNode3->setLeft(root7OfNode2);
	root7OfNode3->setRight(root7OfNode4);
	cout << "Original tree is:" << endl;
	printBST(root7);
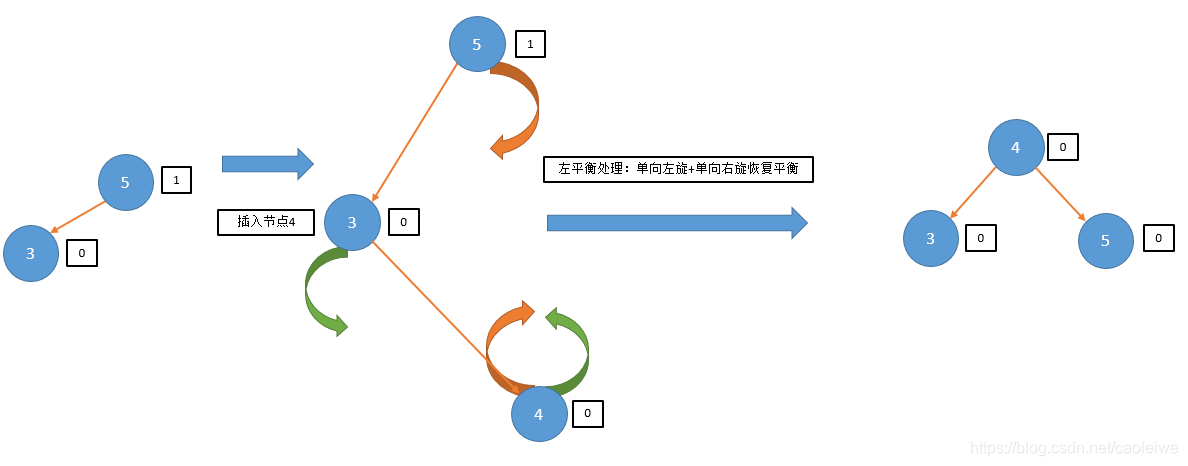
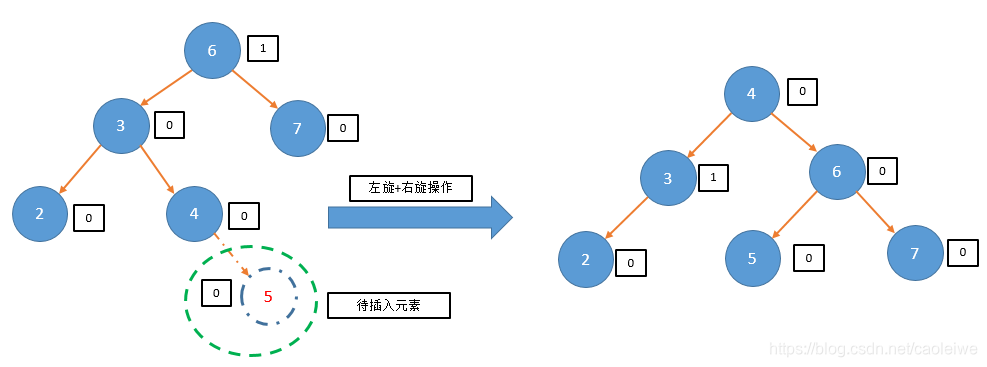
	status = InsertAVL(root7, nullptr, 5, taller3, newroot7);
	cout << "The tree after insertion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newroot7 != nullptr)
	{
		printBST(newroot7);
	}
	else
	{
		printBST(root7);
	}
	cout << "===================example8==============================" << endl;
	bool shorter4 = false;
	BinarySearchNode* newroot8 = nullptr;
	BinarySearchNode* root8 = new BinarySearchNode(20, 0);
	BinarySearchNode* root8OfNode10 = new BinarySearchNode(10, 0);
	BinarySearchNode* root8OfNode30 = new BinarySearchNode(30, -1);
	BinarySearchNode* root8OfNode5 = new BinarySearchNode(5, 0);
	BinarySearchNode* root8OfNode15 = new BinarySearchNode(15, -1);
	BinarySearchNode* root8OfNode25 = new BinarySearchNode(25, 0);
	BinarySearchNode* root8OfNode35 = new BinarySearchNode(35, 0);
	BinarySearchNode* root8OfNode3 = new BinarySearchNode(3, 0);
	BinarySearchNode* root8OfNode7 = new BinarySearchNode(7, 0);
	BinarySearchNode* root8OfNode16 = new BinarySearchNode(16, 0);
	BinarySearchNode* root8OfNode33 = new BinarySearchNode(33, 0);
	BinarySearchNode* root8OfNode37 = new BinarySearchNode(37, 0);
	root8->setLeft(root8OfNode10);
	root8->setRight(root8OfNode30);
	root8OfNode10->setLeft(root8OfNode5);
	root8OfNode10->setRight(root8OfNode15);
	root8OfNode30->setLeft(root8OfNode25);
	root8OfNode30->setRight(root8OfNode35);
	root8OfNode5->setLeft(root8OfNode3);
	root8OfNode5->setRight(root8OfNode7);
	root8OfNode15->setLeft(root8OfNode16);
	root8OfNode35->setLeft(root8OfNode33);
	root8OfNode35->setRight(root8OfNode37);
	cout << "Original tree is:" << endl;
	printBST(root8);
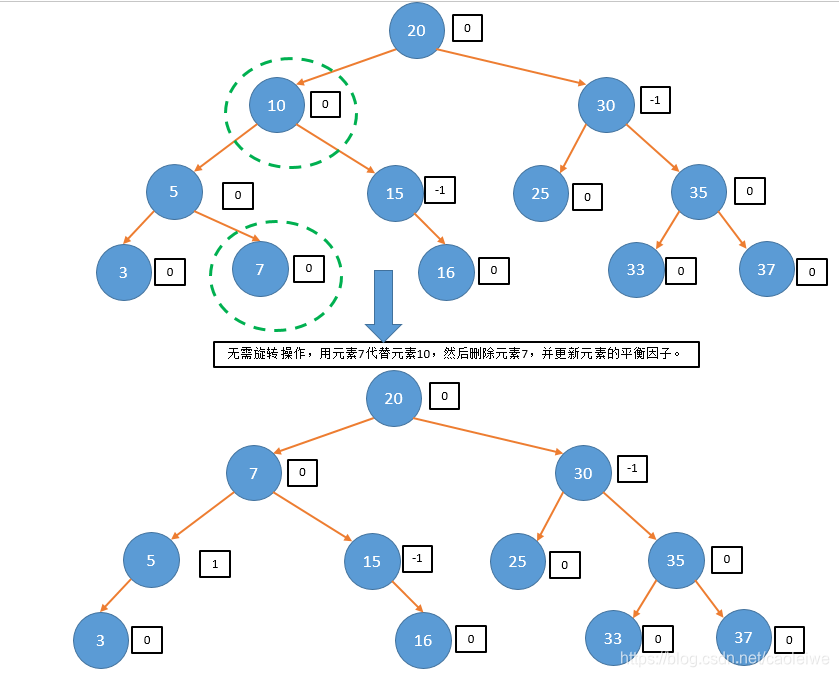
	status = DeleteAVL(root8, nullptr, 10, shorter4, newroot8);
	cout << "The tree after deletion operation is:" << endl;
	cout << "Return status=" << status << endl;
	if (newroot8 != nullptr)
	{
		printBST(newroot8);
	}
	else
	{
		printBST(root8);
	}
}
平衡二叉树---》插入、删除
时间轴
07-24 1万+
平衡二叉树(Balancedbinary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskiiand Landis)于1962年首先提出的，所以又称为AVL树。 定义：平衡二叉树或为空树,或为如下性质的二叉排序树:  （1）左右子树深度之差的绝对值不超过1;  （2）左右子树仍然为平衡二叉树.         平衡二叉树可以避免排序二叉树深度上的极度恶化，使树的高度维持在
平衡二叉树的插入与删除
pjmike的博客
08-09 9106
定义 AVL树是带有平衡条件的二叉查找树。它要求在AVL树中任何节点的两个子树的高度(高度是指节点到一片树叶的最长路径的长) 最大差别为1,如下图所示: 为什么有AVL树 大多数BST操作，例如搜索，最大，最小，插入，删除等，消耗取O（h）时间，h是BST的高度。对于倾斜的二叉树，这些操作的成本可能会变成O(n)。 如果我们在每次插入和删除之后确保树的高度保持O（Logn），那么我...
平衡二叉树的插入和删除
06-08
自己整了一天写的平衡二叉树的插入和删除,暂时还没发现bug...
数据结构------二叉平衡树（二）删除操作
kkxgx的专栏
08-15 3612
二叉平衡树的删除与插入类似，先采用二叉搜索树的删除方法，删除结点，再在必要时通过重新平衡，恢复平衡性和排序性。当删除X有两个孩子时，使用替代法，将问题转化为删除只有一个孩子的结点的问题，然后删除之。由q指向实际被删除的结点，它最多只有一个非空子树，当结点q由它的孩子取代后，该树变矮，这种情况会影响其祖先的平衡性，应重新平衡。使用short变量来记录对其双亲（p）平衡性的影响。 同插入的情况一样，
平衡二叉树
weixin_43987915的博客
02-23 210
平衡二叉树 与二叉搜索树不同之处是结点结构里多了平衡因子 balance factor : 绝对值(左子树的高度-右子树的高度) 定义 要么是二叉搜索树要么是空树 左右子树的高度差不超过一 左右子树都是平衡二叉树 高度的定义 叶结点高度为 1 树的高度等于左子树高度与右子树高度的最大值 操作 1. 插入 平衡二叉树插入结点后可能会导致失衡 此时就要调整离插入结点最近的失衡的树 , 失衡的四种情况有不同的应对方式 左单旋 : 失衡的树的左子树的左子树比较高 让 leftHeight-1, r
二叉搜索树的插入与删除(详细解析)
01-01
题目：创建一个类，类中的数据成员时一棵二叉搜索树，对外提供的接口有添加结点和删除结点这两种方法。用户不关注二叉树的情况。要求我们给出这个类的结构以及实现类中的方法。 思路添加结点：添加结点其实很容易，...
平衡二叉搜索树插入与删除（AVL）
ydg的博客
08-03 929
1.为何要引入平衡二叉搜索树 我们知道，二叉搜索树(BST)已经有比较好的查找，插入和删除的效率。但是为什么不满足于二叉搜索树呢？我们来看一种情况，如图1-1： 从中可以看到，该树仍满足二叉搜索树的定义，但是，查找效率已经从O（）退化为O（n）级别。变成的了一个链表了。我们看到引起这种变化的根本原因是深度的加深和左右子树失衡导致的。平衡二叉树为了解决这种失衡导致算法效率的退化。 2.AVL树的定义 平衡因子：在满足二叉搜索树的条件下，对任意结点其左右子树的深度...
Python实现AVL树：自平衡二叉搜索树的构建与维护
最新发布
11-05
AVL树是一种自平衡二叉搜索树，其主要特点是在每次插入或删除节点后，都会保持树的平衡。树的平衡是通过节点的平衡因子来控制的，平衡因子是该节点左子树的高度与右子树的高度之差。为了确保树的平衡，AVL树要求每个...
Java创建二叉搜索树,实现搜索,插入,删除的操作实例
08-28
Java 创建二叉搜索树、实现搜索、插入、删除的操作实例 Java 创建二叉搜索树是指通过 Java 语言实现一个二叉搜索树数据结构，该树具有查找、插入、删除等操作的功能。二叉搜索树是一种特殊的二叉树，每个节点的值...
【数据结构】AVL树——平衡二叉搜索树
2301_79796701的博客
05-25 1913
平衡树：左子树的高度等于右子树的高度不平衡树：左子树的高度不等于等于右子树的高度二叉搜索树很难是一颗平衡树。对二叉树进行插入和删除的操作，或插入大量的数据不够随机，都会是使二叉搜索树不够平衡。极端情况下，二叉树会退化成类似链表的结构，那么二叉搜索树查询数据的效率荡然无存。在二叉树的基础上加入平衡的概念就是平衡二叉搜索树，也叫AVL树。AVL树也不是一颗绝对的平衡树，AVL树的平衡是相对的，它允许左子树和右子树的高度为 1 ，但不能超过 1。
平衡二叉树（旋转操作，插入，删除，合并，分裂，凹入表打印）
01-12
一个详细的课程设计，包含了旋转操作，插入，删除，合并，分裂，凹入表打印等重点操作。验证所有非法操作，分享给大家学习。
平衡二叉树【AVL树】——插入、删除
yyy_zxc的博客
07-07 376
1、平均查找长度（树高）: 2、结点的平衡因子=左子树高-右子树高平衡二叉树结点的平衡因子只可能是0,1或-1 2、插入 2.1 每次调整的对象都是“最小不平衡子树” 2.2 调整最小不平衡子树A ①LL【A的左孩子右上旋】：在A的左孩子的左子树中插入导致不平衡 ②RR【A的右孩子左上旋】：在A的右孩子的右子树中插入导致不平衡 ③LR【A的左孩子的右孩子先左上旋再右上旋】：
【数据结构】平衡二叉树（插入、查找、删除）解析+完整代码
m0_61628700的博客
05-14 3062
平衡二叉树，简称平衡树（AVL树）树上任一结点的左右子树高度差不超过1。结点的平衡因子=左子树高-右子树高。
平衡二叉树的定义及基本操作（查找、插入、删除）及代码实现
薛定谔的猫的博客
08-12 4989
文章目录平衡二叉树的定义平衡二叉树的插入 平衡二叉树的定义  为了避免树的高度增长过快，降低二叉排序树的性能，我们规定在插入和删除二叉树结点时，要保证在任意结点的左、右子树高度差的绝对值不超过1，将这样的树称为平衡二叉树（Balanced Binary Tree），简称平衡树（AVL）。  定义结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只可能是-1，0或1 。 平衡二叉树可定义为：  或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和
AVL Tree 平衡二叉树基本插入删除节点功能的实现
热门推荐
霖林烟雨
09-18 1万+
简述： 实现AVL 树，主要是两个功能 ： 插入某节点和删除某节点 AVL Tree的定义， 1. 是一棵二叉搜索树（故而每个节点是惟一的, 如果出现重复数字会破坏平衡树的算法） 2. 每个节点左右子树的高度之差（平衡因子）相差最多为1 实现： 为了使所得的二叉树为平衡二叉树， 首先在BSTNode中加了一个计算节点高度的方法getHeight()， 当两个节点高度相
平衡二叉树-插入、删除(java代码)
weixin_37607613的博客
03-30 1844
二叉树定义 目录 一、概念 1、定义 2、平衡因子 3、最小不平衡子树 二、旋转纠正 1、旋转方式 2、旋转纠正类型 LL型 LR型 RR型 RL型 三、插入 四、删除 五、完整代码实现 一、概念 1、定义 规定任意结点的左右子树高度差不大于1，左右子树也是平衡二叉树 2、平衡因子 定义：左子树和右子树高度差 计算：左子树高度 - 右子树高度的值 别名：简称 BF（Balance Factor） 一般来说 BF 的绝对值大于 1，,平衡树二叉树就失衡，需要
树——平衡二叉树插入和查找的JAVA实现(2):增加删除方法
weixin_34092370的博客
03-31 65
package com.tomsnail.data.tree; /** * AVL二叉平衡树 * @author tomsnail * @date 2015年3月30日 下午4:35:50 */ public class AVLTree { /** * 根节点 * @author tomsnail * @date 2...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

qqssss121dfd

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值