PRML Chapter 07 Sparse Kernel Machines

PRML Chapter 07 Sparse Kernel Machines

第六章提到的核函数和核方法，有一个显著的问题，即核函数$k(x_n,x_m)$必须对所有的数据点都进行求值，这对于训练阶段是不可接受的，对于预测阶段，同样也是不可以接受的。因此，我们可以考虑使用稀疏核机(Sparse kernel machines)，这种方法的一个典型特征是训练得到的模型仅仅依赖于少数几个数据点(也称支持向量)，因此被叫做稀疏核机。

Support vector machine

支持向量机(Support vector machine)是一种典型的稀疏核机。考虑数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{ (x_1,y_1),(x_2,y_2),...,(x_m,y_m) \} D={(x1​,y1​),(x2​,y2​),...,(xm​,ym​)}， y i ∈ { − 1 , 1 } y_i \in \{ -1, 1 \} yi​∈{−1,1}。分类学习最基本的想法就是基于训练集$D$在样本空间中找到一个划分超平面，将不同类别的样本尽量区分开来，但这样的超平面通常很多，支持向量机通过最大间隔(margin)的方法选出最优超平面。

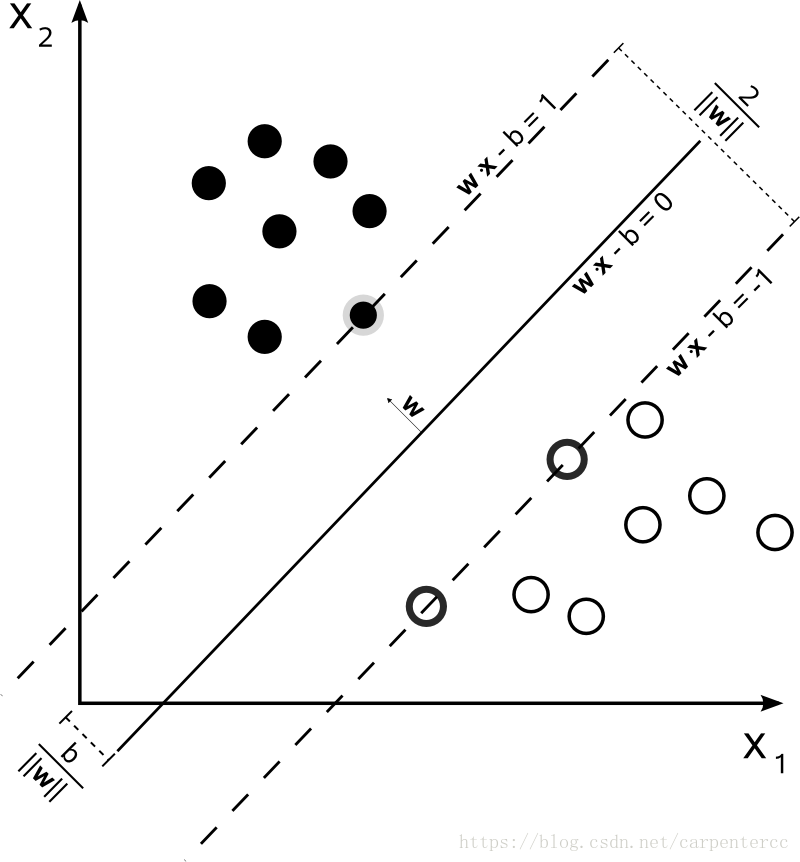
现在，考虑超平面${\mathbf{\omega }}^T\mathbf{x}+b=0$能够将所有的数据点都正确的分类，如上图所示。可以看到，距离超平面最近的这几个训练样本点使得式(7.1)成立，

$$\{\begin{array}{l}{\mathbf{\omega }}^T{\mathbf{x}}_i+b\ge +1,y_i=+1\\ {\mathbf{\omega }}^T{\mathbf{x}}_i+b\le -1,y_i=-1\end{array}\text{\hspace{1em}(7.1)}$$

因此，他们被称为支持向量(support vector)，两个异类支持向量到超平面的距离之和为，

$$\gamma =\frac{2}{||\mathbf{\omega }||}\text{\hspace{1em}(7.2)}$$

式(7.2)被称为间隔，欲找到最大间隔(maximum margin)的划分超平面，也就是要找到能满足式(7.1)中约束的参数$\mathbf{\omega },b$，使得式(7.2)中的$\gamma$最大，即，

$$\begin{gathered} \underset{\mathbf{\omega },b}{\max }\frac{2}{||\mathbf{\omega }||} \\ s.t.y_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,...,m\text{\hspace{1em}(7.3)} \end{gathered}$$

式(7.3)等价于

$$\begin{gathered} \underset{\mathbf{\omega },b}{\max }\frac{1}{2}||\mathbf{\omega }|{|}^2 \\ s.t.y_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,...,m\text{\hspace{1em}(7.4)} \end{gathered}$$

由于式(7.4)本身就是一个凸二次规划问题，因此可以直接用现成的优化算法计算其最优解，但通常使用其对偶形式，更加高效的进行计算。考虑使用拉格朗日乘子${\alpha }_i\ge 0$，其对偶形式可以写为，

$$\begin{gathered} \underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ {\alpha }_i\ge 0,i=1,2,..,m\text{\hspace{1em}(7.5)} \end{gathered}$$

一般来说，使用SMO(sequential Minimal Optimization)对其进行高效的求解。上述关于SVM的讨论都假设数据点线性可分，但是实际中往往会有类别重叠的情况发生，因此，我们可以引入软间隔(soft margin)的概念，使得一个数据点可以不满足约束，

$$y_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)\ge 1\text{\hspace{1em}(7.6)}$$

从而，优化目标可以变为，

$$\underset{\mathbf{\omega },b}{\min }\frac{1}{2}||\mathbf{\omega }|{|}^2+C\sum _{i=1}^{m}L(y_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)-1)\text{\hspace{1em}(7.7)}$$

其中，$L$是损失函数，$C$则作为惩罚参数，当其趋近于无穷大时，迫使所有样本都满足式(7.6)，当其为有限值时，式(7.7)允许一些样本不满足约束。引入松弛变量(slack variables)代替损失函数，则软间隔支持向量机可以表示为，

$$\begin{gathered} \underset{\mathbf{\omega },b,{\xi }_i}{\min }\frac{1}{2}||\mathbf{\omega }|{|}^2+C\sum _{i=1}^m{\xi }_i \\ s.t.y_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i \\ {\xi }_i\ge 0,i=1,2,...,m\text{\hspace{1em}(7.8)} \end{gathered}$$

Support vector regression

支持向量回归(Support vector regression)，是一种利用支持向量进行回归预测的方法。考虑我们需要拟合的函数为，

$$f(\mathbf{x})={\mathbf{\omega }}^T\varphi (\mathbf{x})\text{\hspace{1em}(7.9)}$$

则，支持向量回归希望能够找到$f(\mathbf{x})$，其与真实值$y$的偏差为$ϵ$。这显然可以看作是以$f(\mathbf{x})$为中心，构建一个宽度为$2ϵ$的间隔带，若数据点落入此间隔带，则认为被预测正确，因此，其具体形式可以表示为，

$$\underset{\mathbf{\omega },b}{\min }\frac{1}{2}||\mathbf{\omega }|{|}^2+C\sum _{i=1}^m{L}_{ϵ}(f(\mathbf{x})-y_i)\text{\hspace{1em}(7.10)}$$

引入松弛变量${\xi }_i,\widehat{{\xi }_i}$，可以将上式重写为，

$$\begin{gathered} \underset{\mathbf{\omega },b,{\xi }_i,\widehat{{\xi }_i}}{\min }\frac{1}{2}||\mathbf{\omega }|{|}^2+C\sum _{i=1}^m({\xi }_i+\widehat{{\xi }_i}) \\ s.t.f(\mathbf{x})-y_i\le ϵ+{\xi }_i \\ {y}_i-f(\mathbf{x})\le ϵ+\widehat{{\xi }_i} \\ {\xi }_i\ge 0,\widehat{{\xi }_i}\ge 0,i=1,2,...,m\text{\hspace{1em}(7.11)} \end{gathered}$$