来源:光的角动量 第一章 第二章部分:SAM和OAM的基本性质 - 知乎 (zhihu.com),仅作为个人学习笔记(个人存档)。

1. 简介
在 Poynting 的开创性工作以及 Beth 的首次实验验证之后,角动量被认为是光的重要特征之一。
- 这些工作考虑了由光束的圆偏振产生的自旋角动量。
1992 年,Allen 等人的一篇论文开启了对光学领域的角动量的研究的新时代。
- 这项工作描述了所谓的涡旋光中的轨道角动量,并且很快被实验验证。此后,对光的角动量的研究就发展为了一个庞大的研究领域,在光学操控、量子信息、光子学、等离激元学以及天体物理学中都有很多的应用。
- 这其中重要的原因是,光的自旋、轨道角动量是可以单独观察的属性,也就是说自旋角动量、轨道角动量是可分的。
— —例如,在同轴单色光中、将轨道角动量分解成自旋角动量和轨道角动量是很直接的。
— —另一方面,量子电动力学和场论的基本困难导致在处理更一般的非同轴光、非单色光中的自旋角动量、轨道角动量时候、遭遇到一些微妙的困难。
— —尽管如此,自旋角动量、轨道角动量的分解仍然是可能的,并且在光学中具有重要的物理意义,我们将在这篇综述中会用到。
- 自旋角动量和光的偏振有关。
— —准轴光束中的右旋圆偏光和左旋圆偏光分别对应于螺度等于正负一的情况,即 。
— —从普通物理学、光子的量子力学描述中我们知道,光的自旋角动量和光的传播方向一致。
— —如果光束的平均动量 及其平均波矢
存在关系
,这时我们可以称这束光携带自旅角动量
(1.1)
式中,是螺度。
- 与之相反地,无偏振的准轴光束的轨道角动量与偏振无关,它由电磁场的标量波函数中的相位及动量环流产生。
eg.轨道角动量的实例
- 所谓的光涡旋,是指具有一个螺旋相位分布的奇点,它会产生一个局域动量密度(即相位的梯度)的环流,也因此产生了轨道角动量。
- 单色光场的轨道角动量态都是傍轴涡束,携带有沿着光的传播方向的轨道角动量:
(1.2)
其中 是一个拓扑量子数,称为该涡束的拓扑荷。
- 因此,在我们考虑的大多数情况中,光的角动量总是沿着其平均动量
方向的,也就是说,它是纵向的。
- 然而,最近对关于横向的角动量的研究忽然兴起,这种轨道角动量与光的传播方向 (平均动量方向)正交,更为重要的是,不同类型的横向轨道角动量,无论是自旋角动量还是轨道角动量,从物理性质和起源上讲都有很大的不同。
eg.角动量的物理起源
- 例如,最简单的横向角动量就是一个经典质点的轨道角动量。
— —假设质点的坐标为 ,动量为
,那么其角动量为
(1.3)
— —显然,这个角动量是外在的(与“内禀的”相对),因为它依赖于坐标原点的选取。
- 类似地,另一个外在轨道角动量的例子是由一束与坐标原点偏移一定距离的光束产生的:
(1.4)
其中,是平均位移,也就是光束的位移。
— —尽管它的特征很平庸,在 1987 年,Player 和 Fedoseyev 证明了这种外在的轨道角动量在光学界面处的光学自旋霍尔效应中起了重要的作用,这种效应中光束的位移也被称作Imbert-Fedorov 位移。
— — 我们将在本文中多次讨论外在的横向轨道角动量。
- 不同于前面这些例子,有一种由 Bliokh 和 Nori 在 2012 年第一次描述的横向自族角动量。
— — 这种横向自族在结构光场中以局城的方式出现,例如倏逝波、聚焦光束、双光束干涉等。
— — 横向自旋有很多新奇的性质,这些性质和我们之前已知的光子自旋有很大的不同,它和光波的螺度无关,甚至可以出现在线偏光中( 这就是说,不同的横向自旋轨道角动量具有不同的物理特性,并取决于不同的场参数);另外,这种不依赖于偏振的横向自旋强烈依赖于光的传播方向。
— — 正是由于这些新奇的性质,倏逝波中的横向自旅角动量在依赖自旋的单向光学界面 (unidirectionalopticalinterfaces)中已有很多重要应用。
— — 倏逝波中横向自旋与传播方向的 robust 的耦合是麦克斯韦方程的一个基本属性,它可以与光的量子自旋霍尔效应联系起来。

1.1 约定与记号

2 自旋角动量和轨道角动量:基本属性
2.1 粒子和波
- 我们首先回顾一下质点力学和波动力学中涉及到的角动量概念:-在质点和波这两种体系中,角动量的概念是非常不同的。
- 首先我们考虑一个经典质点,经典质点携带的轨道角动量为
其中 ,
分别是质点的位矢和动量。


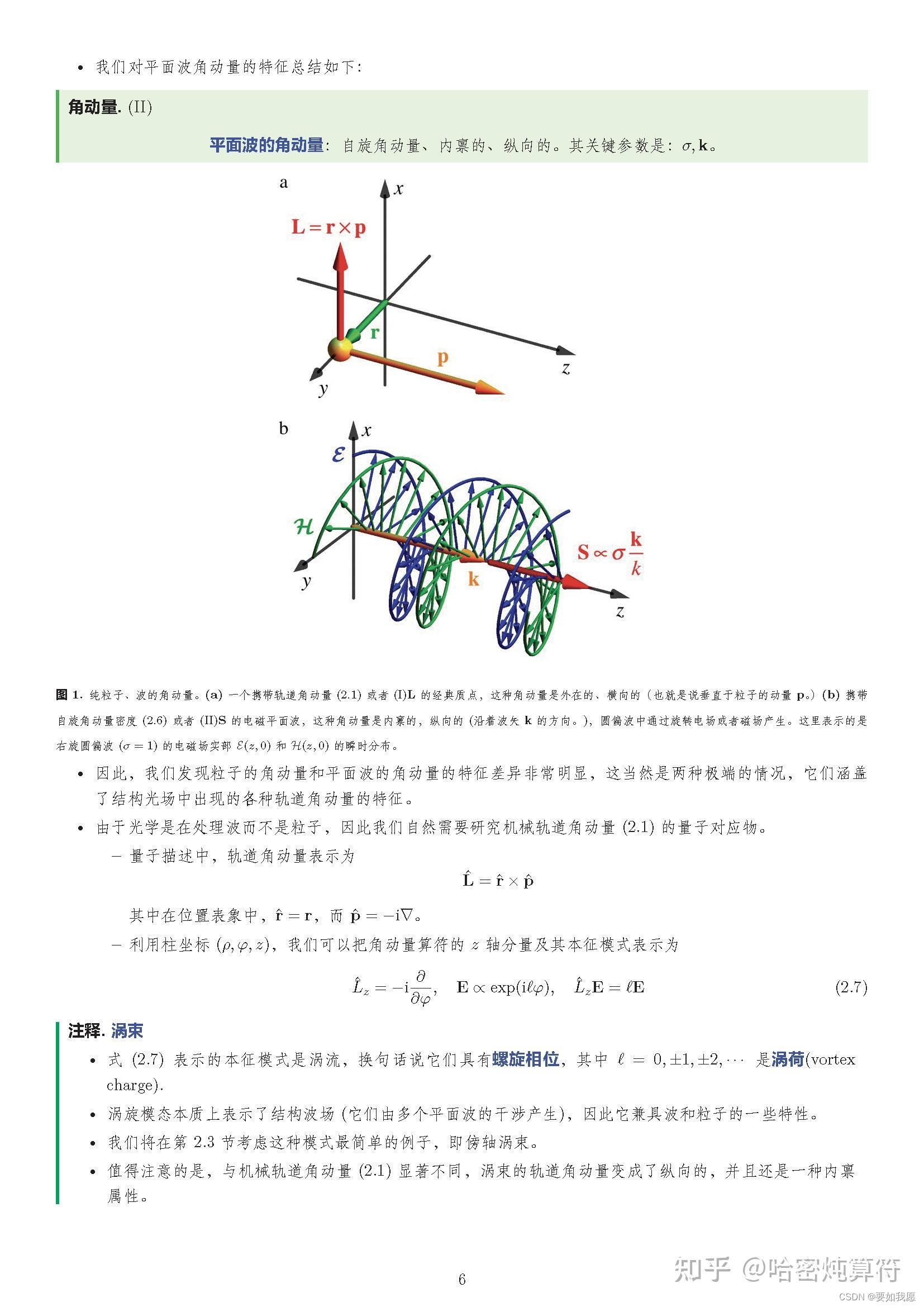
2.2 一般光场的通用属性




























 2883
2883

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








