傅里叶变换去噪

海の云

已于 2023-10-18 18:39:36 修改

阅读量2.1k

点赞数

分类专栏：大数据与机器学习文章标签： ffmpeg

于 2022-12-07 11:50:55 首次发布

大数据与机器学习专栏收录该内容

31 篇文章 1 订阅

订阅专栏

在计算机中用这个公式更好处理一点

在这里插入图片描述

n和N是在一个正弦周期内采样N个点，采样间隔为2pi\N,n用来步进，一次步进2pi\N,最后进行累加求和，就得出了X(k)

最后离散傅里叶变换完整代码
1，从文件读取8000个音频数据，由于现实中的音频没有虚部，所以只设置实部。
2，离散傅里叶变换关键处
temp的re就是对应上图公式的cos，同理im就是对应上图的sin，每个X[k]进行累加求和

   for (int k = 0; k < N; k++)
   {
       X[k].re = 0;
       X[k].im = 0;
       for (int n = 0; n < N; n++)
       {
           temp.re = (float)cos(2 * pi*k*n / N);
           temp.im = -(float)sin(2 * pi*k*n / N);
           X[k] = complexadd(X[k], complexMult(x[n], temp));
       }
   }

3，离散傅里叶逆变换就是X（k）乘上e^(j2tkn/N),也就是实部虚部都为正

temp.re = (float)cos(2 * pi*k*n / N);
temp.im = (float)sin(2 * pi*k*n / N);
x[k] = complexadd(x[k], complexMult(X[n], temp));

下图公式求幅度

在代码中表示

printf("%d ", int(2.0/N*sqrt(X[k].re*X[k].re + X[k].im*X[k].im)));
//打印的为幅度
1
2
完整代码

#include <stdio.h>
#include <math.h>

#define pi 3.1415926
struct complex
{
float re;
float im;
};

complex complexadd(complex a, complex b) { //复数加
   complex rt;
   rt.re = a.re + b.re;
   rt.im = a.im + b.im;
   return rt;
}

complex complexMult(complex a, complex b) { //复数乘
   complex rt;
   rt.re = a.re*b.re - a.im*b.im;
   rt.im = a.im*b.re + a.re*b.im;
   return rt;
}
complex complexSet(complex *a, short *b, int N)//复数设置
{
   for (int i = 0; i < N; i++)
   {
       a[i].re = b[i];
       a[i].im = 0;
   }
}

//离散傅里叶变换
//X[]标识变换后频域，x[]为时域采样信号
void dft(complex X[], complex x[], int N)
{
   complex temp;
   int k, n;
   for (int k = 0; k < N; k++)
   {
       X[k].re = 0;
       X[k].im = 0;
       for (int n = 0; n < N; n++)
       {
           temp.re = (float)cos(2 * pi*k*n / N);
           temp.im = -(float)sin(2 * pi*k*n / N);
           X[k] = complexadd(X[k], complexMult(x[n], temp));
       }
       printf("%d ", int(2.0/N*sqrt(X[k].re*X[k].re + X[k].im*X[k].im)));
//打印的为幅度
       if (k >= 6000)//去除高频信号
       {
           X[k].re = 0.0;
           X[k].im = 0.0;
       }
   }
}
//离散傅里叶逆变换
//X[]标识变换后频域，x[]为时域采样信号
void idft(complex X[], complex x[], int N) {
   complex temp;
   //int k, n;
   for (int k = 0; k < N; k++)
   {
       x[k].re = 0;
       x[k].im = 0;
       for (int n = 0; n < N; n++)
       {
           temp.re = (float)cos(2 * pi*k*n / N);
           temp.im = (float)sin(2 * pi*k*n / N);
           x[k] = complexadd(x[k], complexMult(X[n], temp));
       }
       x[k].re /= N;
       x[k].im /= N;
   }
}

#define N 8000//采样率为8000
int main() {
   complex samples[N], X[N], x[N]; //原始数据，变换后的频域数据，逆变换后的时域数据
   FILE *fp;
   FILE *fp2;
   short buf[N];
   int re=0;
   fp=fopen("./ttt.pcm", "rb");
   fp2 = fopen("./trans.pcm", "wb");
   if (!fp ||!fp2) {
       printf("I could not open file.\n");
       return 1;
   }
   else
   {
       while (fread(buf, sizeof(short)*N,1 , fp) > 0)//末尾数据忽略
       {
           complexSet(samples, buf, N);
           dft(X, samples, N);
           idft(X, x, N);
           for (int i = 0; i < N; i++)
           {
               buf[i] = x[i].re;
           }
           fwrite(buf, sizeof(short)*N,1 , fp2);
       }
   }
   fclose(fp);
   fclose(fp2);
   return 0;
}

傅里叶变换

傅里叶变换是用三角函数表示目标函数，傅里叶变换广泛的应用在信号处理、偏微分方程、热力学、概率统计等领域：大到天体观测，小到我们手机中图片、音频应用等，没有傅里叶变换就没有如今丰富多彩的信息化时代。在人工智能领域中，可利用傅里叶变换证明中心极限定理，而中心极限定理是概率学最重要的基石；傅里叶变换本质是将时域的信息汇总到频域中，当两组数据的傅里叶变换结果相同时，称为两者依概率收敛。本章介绍傅里叶变换推导过程并结合代码实现傅里叶变换，按数学推导的离散傅里叶变换算法复杂度较高，本章最后介绍快速傅里叶变换（FFT）的实现原理。

一、傅里叶变换原理

1.1 目标函数f(x)为周期2π的函数

前面的章节中曾用多项式拟合目标函数，傅里叶变换是利用三角函数拟合函数，正弦、余弦函数有以下性质：

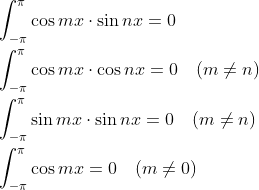
(1)

三角函数集合

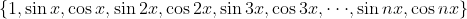
在[-π,π]可以看成函数空间一组正交基,目标函数f(x)可写成傅里叶级数：

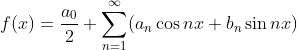
（1.1）

an、bn都是待定系数，也表示f(x)在正交基上的坐标，(1.1)式两边乘以cos mx ，m为一个特定系数坐标，求积分有：

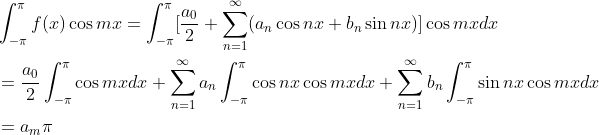
由此可得an:

(1.3)

同样可得bn:

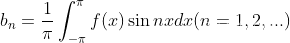
(1.4)

上面函数f(x)周期为2π，如果f(x)是周期为2T，可用线性仿射将f(x)的定义域x投射到t上，t的周期是2π:

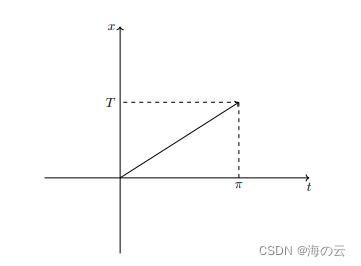
此时有

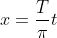
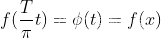, 从上图可见，Φ(t)是在[-∞,∞]一个周期为2π函数，有：

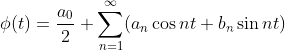
将

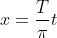
转化为代入上式可得：

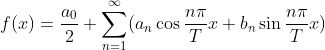
（1.5）

再利用积分求系数an、bn：

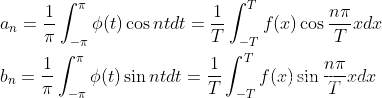
（1.6）

1.2 f(x)非周期函数

f(x)不是周期函数时，可理解为f(x)的周期为+∞，不妨先考虑周期为2T函数fT(x)，T为无限大取极限后，可将fT(x)延拓到周期为+∞函数f(x)，先利用欧拉公式将公式(1.5)变为复数形式：

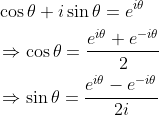
设

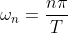
公式(1.5)可表示成：

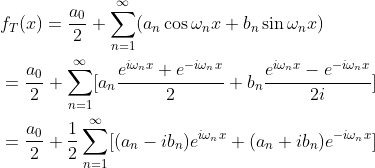
(1.7)

an+ibn和an-ibn是一对共轭复数，幅值相同，相位角在x轴上对称，设cn=an-ibn,利用公式(1.6)得：

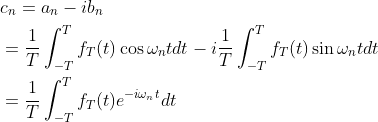
(1.7.1)

cn的共轭

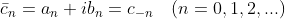
且有：

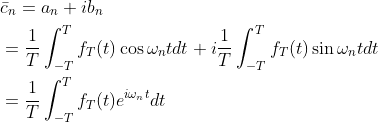
(1.7.2)

公式1.7中n的取值范围是从1到无穷，引入cn后n的取值范围是(-∞,+∞)，1.7式写成下面的形式：

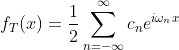
(1.7.3)

1.7.1代入上式后得到fT(x)：

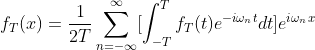
(1.8)

接下来利用式(1.8)将fT(x)周期延拓至∞可得目标函数f(x):

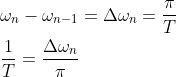
(1.8.1)

式(1.8.1)代入(1.8)得到f(x)极限形式的函数：

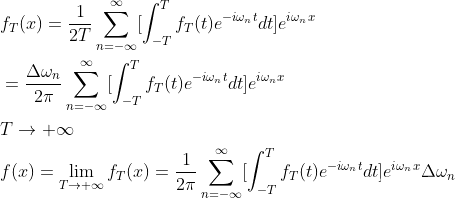
当T为+∞时，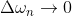

,f(x)此时可表示成积分形式：

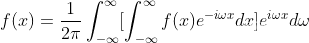
（1.9）

上式中

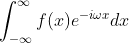
称为原函数f(x)的傅里叶变换，计算积分过程中ω视为符号常量，积分结果是含自变量ω的函数,傅里叶变换可用下面的表示方式：

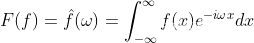
（1.10）

而F(f)再经过一次积分后可还原为f(x),这称为傅里叶逆变换：

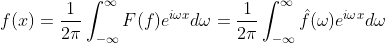
f(x)同样称为时域函数，比如记录每天雨量的变化、每小时道路车辆的流量、汽车每年的里程数等，时域函数是日常生活中大量接触到的函数模型，而1.10式将f(x)经过傅里叶变换后得到是频域的信息，频域单位是赫兹，反应出原函数周期性方面的信息，时域与频域观察世界视角不同，可以用下图来加强对两者的认识。

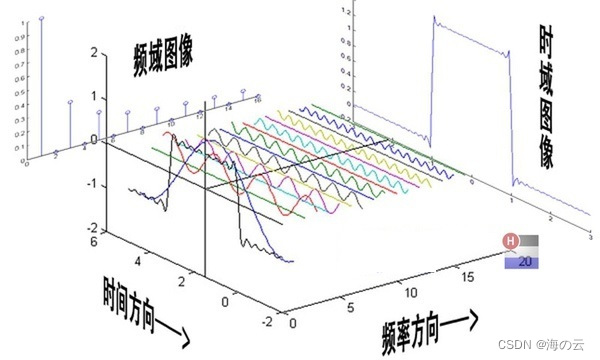
二、程序实现傅里叶变换

2.1 离散傅里叶变换

代码中利用式(1.10)的离散形式实现傅里叶变换,设在定义域内选择N个数据实现f(x)函数离散化，f(x)可表示成：

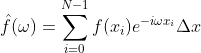（2）

如果f(x)表示的是一个信号，所选择的时间段为一秒即单位时间，那么N称为采样频率，由采样定理可知，采样频率至少是信号最大频率的2倍，就傅里叶变换而言，采样频率最好是2的整数倍，有了这些设定后公式（2）可表示为：

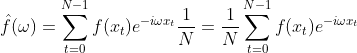
(2.1)

上式用

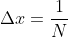
将单位时间一秒分成N份，在傅里叶变换中也称归一化，2.1式中ω代表角速度，通常将角速度处理成频率形式，频率h与角速度的关系有：

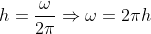
上式代入2.1后有：

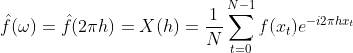（2.2）

X(h)是单位为赫兹的频域函数，再回头看公式1.7.3，参数cn中的n取值范围是(-∞,+∞),也就是说原公式中是允许有负角速度或者说负频率存在的，而(2.2)式中n是非负整数，代表着客观物理世界中没有所谓的负频率，这是数学与物理的差异性导致的，(2.2)引入负频率才能满足傅里叶变换公式，幸运的是正频率与负频率是共轭的关系，即cn与

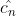
关系，两者的幅值是一样的，傅里叶离散变换的目标是得到每个频率对应幅值，所以将（2.2）乘以2即可得到与1.7.3式一样的定义。

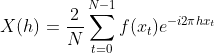
(2.3)

下面代码利用公式2.3实现傅里叶离散变换，目标函数(原始信号)为：

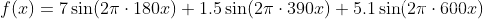
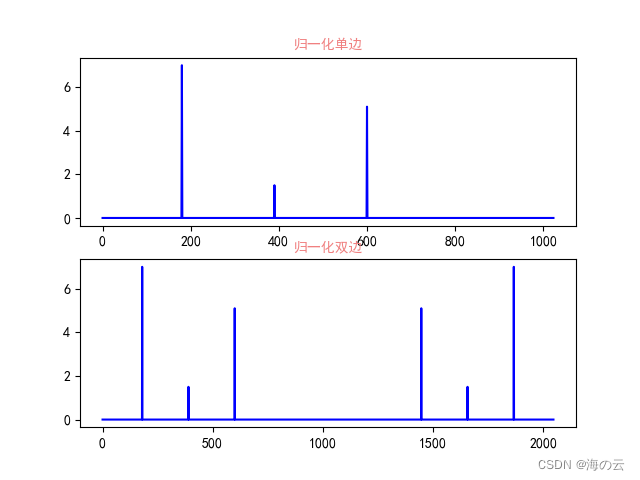
原始信号含有频率为180、390、600Hz的信号，采用频率为2048Hz,对应幅值分别为7、1.5、5.1。

import numpy as np

from scipy.fftpack import fft,ifft

import matplotlib.pyplot as plt

from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文

mpl.rcParams['axes.unicode_minus'] = False # 显示负号

Samplingfq=2048

def loadsignal(N ):

# 采样点选择1400个，因为设置的信号频率分量最高为600Hz，根据采样定理知采样频率要大于信号频率2倍，所以这里设置采样频率为1400Hz（即一秒内有1400个采样点）

x = np.linspace(0, 1, N)

# 设置需要采样的信号，频率分量有180，390和600

y = 7 * np.sin(2 * np.pi * 180 * x) + 1.5 * np.sin(2 * np.pi * 390 * x) + 5.1 * np.sin(2 * np.pi * 600 * x)

return x,y

def FourierTransform():

x, y = loadsignal(Samplingfq)

ffts=[]

for i in range(Samplingfq):

real=0

imag=0

for t in range(Samplingfq):

real=real+y[t]* np.cos(2*np.pi*i*x[t])*2/Samplingfq

imag=imag+y[t]* np.sin(2*np.pi*i*x[t])*-2/Samplingfq

ffts.append([i,np.sqrt(real**2+imag**2) ])

ffts=np.array(ffts)

plt.subplot(211)

plt.plot(range(int(Samplingfq/2)), ffts[:int(Samplingfq/2),1] , 'b')

plt.title('归一化单边', fontsize=10, color='#F08080')

plt.subplot(212)

plt.plot(range(Samplingfq), ffts[:, 1] , 'b')

plt.title('归一化双边', fontsize=10, color='#F08080')

plt.show()

if __name__ == '__main__':

FourierTransform()