转载自:http://www.learnopencv.com/head-pose-estimation-using-opencv-and-dlib/
姿态估计
定义
计算机视觉领域的姿态估计用目标相对于摄像机的平移量和旋转矩阵进行表示。
计算机视觉领域将姿态估计问题当作N个点的透视变化问题(Perspective-n-Point,PNP),解决方案是对于一个标定好的摄像机,根据目标在3维世界坐标系中n个点的坐标和对应投影到2维图像坐标系中的点集之间的变换关系矩阵进行求解。
相机运动
3D刚性目标相对于摄像机只有两种运动关系,即平移和旋转。
平移
将一个3维点 (X,Y,Z) ( X , Y , Z ) 变换到另一个3维点 (X′,Y′,Z′) ( X ′ , Y ′ , Z ′ ) ,平移有3个坐标系上的自由度参数,可以用一个向量 t t 进行表示。
旋转
同样可以沿着X,Y,Z三个轴进行旋转。可以用一个3*3的旋转矩阵或欧拉角(roll,pitch,yaw)进行表示。
姿态估计所需的输入信息
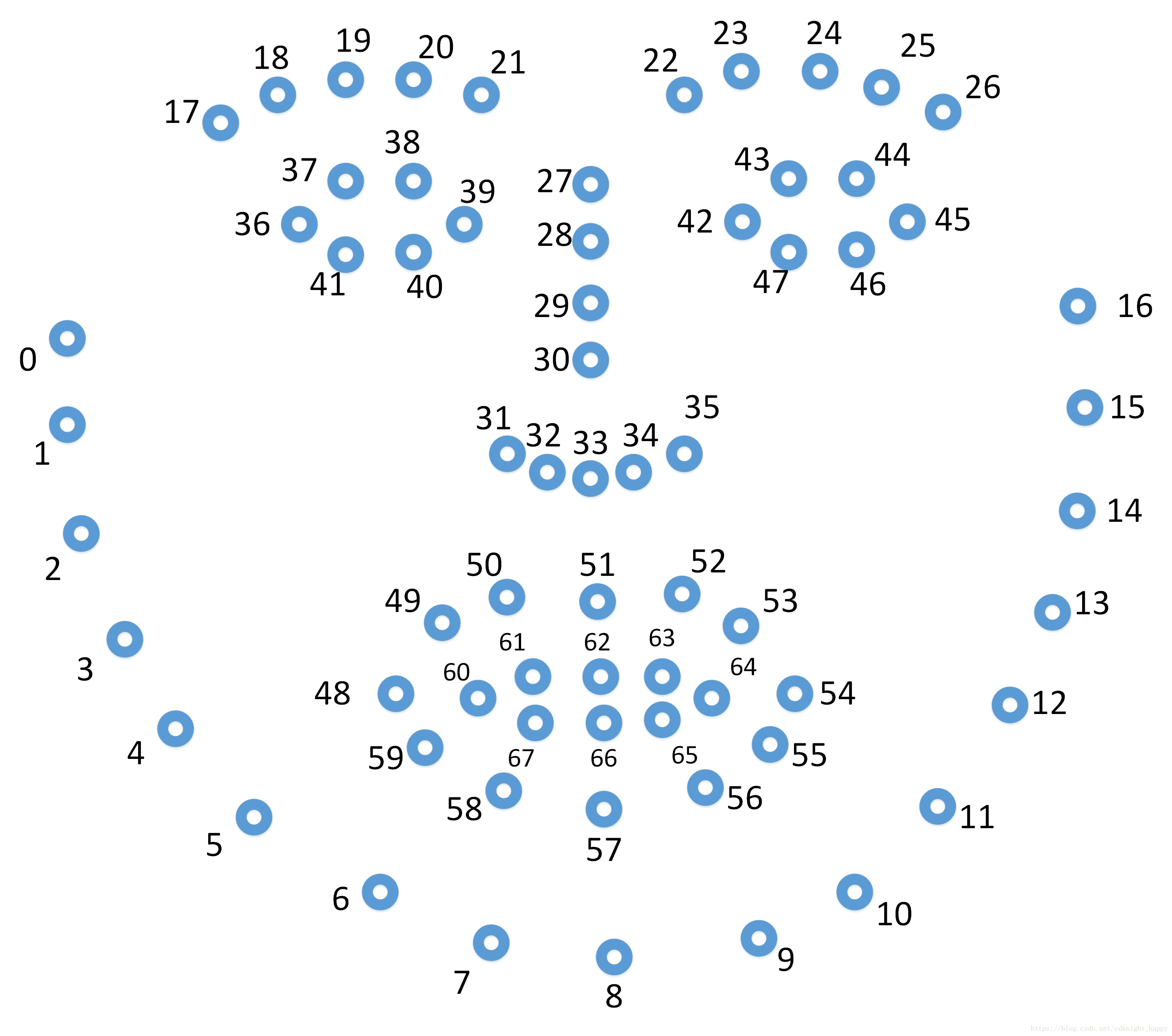
人脸68个关键点分布图
- 数个2维坐标点坐标
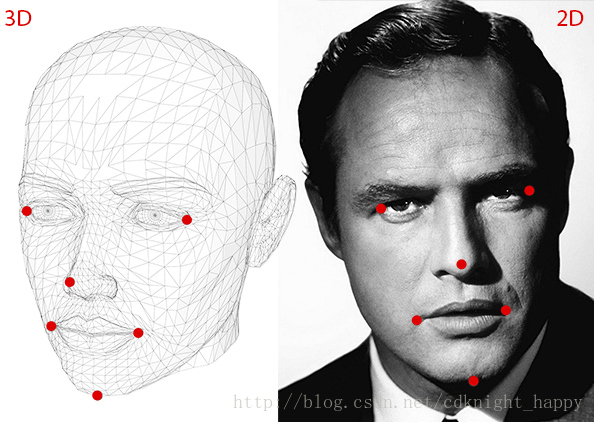
使用人脸特征点检测算法对二维人脸图像进行特征点检测。本文中,作者使用鼻尖、下巴、左眼左眼角、右眼右眼角、左嘴角和右嘴角的坐标。 - 和每个2维坐标点对应的3维坐标
在实际应用中,不需要获取一个精确的人脸三维模型并且也没法获取这样的模型,因此,作者设置了上述6个二维点对应的3维坐标,分别为:
Tip of the nose : ( 0.0, 0.0, 0.0)
Chin : ( 0.0, -330.0, -65.0)
Left corner of the left eye : (-225.0f, 170.0f, -135.0)
Right corner of the right eye : ( 225.0, 170.0, -135.0)
Left corner of the mouth : (-150.0, -150.0, -125.0)
Right corner of the mouth : (150.0, -150.0, -125.0) - 相机的内参数矩阵
进行相机参数估计时首先需要对相机进行标定,精确的相机标定需要使用张正友的棋盘格标定,这里还是进行近似。相机的内参数矩阵需要设定相机的焦距、图像的中心位置并且假设不存在径向畸变。这里设置相机焦距为图像的宽度(以像素为单位),图像中心位置为(image.width/2,image.height/2).
如何进行姿态估计
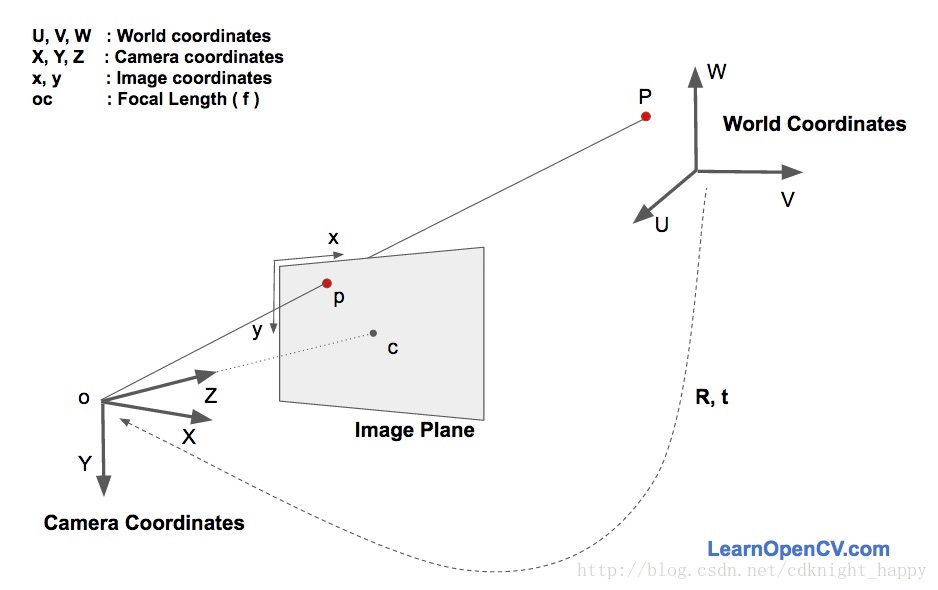
姿态估计过程中有三个坐标系,分别为世界坐标系、相机坐标系和图像坐标系。一个世界坐标系中的三维点通过旋转矩阵
R
R
和平移向量映射到相机坐标系
(X,Y,Z)
(
X
,
Y
,
Z
)
,一个相机坐标系中的三维点
(X,Y,Z)
(
X
,
Y
,
Z
)
通过相机的内参数矩阵映射到图像坐标系
(x,y)
(
x
,
y
)
。
Direct Linear Transform
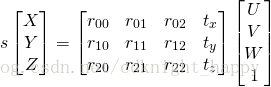
上述类似于线性但是多一个系数s的问题需要通过DLT方法进行解决。
LM最优化
上述DLT方法精确度不足,主要有两个原因,一是旋转矩阵R有三个自由度但是DLT方法中用9个数字进行表示,DLT方法中没有限制该3*3矩阵必须为旋转矩阵;更重要的是,DLT方法中没有最小化正确的目标函数。
解决办法是使用LM最优化方法最小化投影误差。可以先随机的选取矩阵R和向量t,将3维世界坐标系中的6个点映射到二维图像坐标系中,然后计算映射点和通过特征点提取算法提取的二维坐标点之间的误差,通过迭代减小映射误差可以得到更精确的R和t。
OpenCV solvePnP
opencv中可以通过solvePnP和solvePnPRansac函数进行姿态估计。
C++: bool solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=SOLVEPNP_ITERATIVE )
Python: cv2.solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]) → retval, rvec, tvec
Parameters:
objectPoints – Array of object points in the world coordinate space. I usually pass vector of N 3D points. You can also pass Mat of size Nx3 ( or 3xN ) single channel matrix, or Nx1 ( or 1xN ) 3 channel matrix. I would highly recommend using a vector instead.
imagePoints – Array of corresponding image points. You should pass a vector of N 2D points. But you may also pass 2xN ( or Nx2 ) 1-channel or 1xN ( or Nx1 ) 2-channel Mat, where N is the number of points.
cameraMatrix – Input camera matrix A =
distCoeffs – Input vector of distortion coefficients (k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6],[s_1, s_2, s_3, s_4]]) of 4, 5, 8 or 12 elements. If the vector is NULL/empty, the zero distortion coefficients are assumed. Unless you are working with a Go-Pro like camera where the distortion is huge, we can simply set this to NULL. If you are working with a lens with high distortion, I recommend doing a full camera calibration.
rvec – Output rotation vector.
tvec – Output translation vector.
useExtrinsicGuess – Parameter used for SOLVEPNP_ITERATIVE. If true (1), the function uses the provided rvec and tvec values as initial approximations of the rotation and translation vectors, respectively, and further optimizes them.
flags –
Method for solving a PnP problem:
SOLVEPNP_ITERATIVE Iterative method is based on Levenberg-Marquardt optimization. In this case, the function finds such a pose that minimizes reprojection error, that is the sum of squared distances between the observed projections imagePoints and the projected (using projectPoints() ) objectPoints .
SOLVEPNP_P3P Method is based on the paper of X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang “Complete Solution Classification for the Perspective-Three-Point Problem”. In this case, the function requires exactly four object and image points.
SOLVEPNP_EPNP Method has been introduced by F.Moreno-Noguer, V.Lepetit and P.Fua in the paper “EPnP: Efficient Perspective-n-Point Camera Pose Estimation”.
The flags below are only available for OpenCV 3
SOLVEPNP_DLS Method is based on the paper of Joel A. Hesch and Stergios I. Roumeliotis. “A Direct Least-Squares (DLS) Method for PnP”.
SOLVEPNP_UPNP Method is based on the paper of A.Penate-Sanchez, J.Andrade-Cetto, F.Moreno-Noguer. “Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation”. In this case the function also estimates the parameters f_x and f_y assuming that both have the same value. Then the cameraMatrix is updated with the estimated focal length.
OpenCV solvePnPRansac
使用Ransac方法可以减小噪声点的干扰。Ransac方法随机的选取点估计参数,然后选取能够得到最大内点数的参数作为最优估计参数。
C++: void solvePnPRansac(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int iterationsCount=100, float reprojectionError=8.0, int minInliersCount=100, OutputArray inliers=noArray(), int flags=ITERATIVE )
Python: cv2.solvePnPRansac(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, iterationsCount[, reprojectionError[, minInliersCount[, inliers[, flags]]]]]]]]) → rvec, tvec, inliers
iterationsCount – The number of times the minimum number of points are picked and the parameters estimated.
reprojectionError – As mentioned earlier in RANSAC the points for which the predictions are close enough are called “inliers”. This parameter value is the maximum allowed distance between the observed and computed point projections to consider it an inlier.
minInliersCount – Number of inliers. If the algorithm at some stage finds more inliers than minInliersCount , it finishes.
inliers – Output vector that contains indices of inliers in objectPoints and imagePoints .
实现
c++
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main(int argc, char **argv)
{
// Read input image
cv::Mat im = cv::imread("headPose.jpg");
// 2D image points. If you change the image, you need to change vector
std::vector<cv::Point2d> image_points;
image_points.push_back( cv::Point2d(359, 391) ); // Nose tip
image_points.push_back( cv::Point2d(399, 561) ); // Chin
image_points.push_back( cv::Point2d(337, 297) ); // Left eye left corner
image_points.push_back( cv::Point2d(513, 301) ); // Right eye right corner
image_points.push_back( cv::Point2d(345, 465) ); // Left Mouth corner
image_points.push_back( cv::Point2d(453, 469) ); // Right mouth corner
// 3D model points.
std::vector<cv::Point3d> model_points;
model_points.push_back(cv::Point3d(0.0f, 0.0f, 0.0f)); // Nose tip
model_points.push_back(cv::Point3d(0.0f, -330.0f, -65.0f)); // Chin
model_points.push_back(cv::Point3d(-225.0f, 170.0f, -135.0f)); // Left eye left corner
model_points.push_back(cv::Point3d(225.0f, 170.0f, -135.0f)); // Right eye right corner
model_points.push_back(cv::Point3d(-150.0f, -150.0f, -125.0f)); // Left Mouth corner
model_points.push_back(cv::Point3d(150.0f, -150.0f, -125.0f)); // Right mouth corner
// Camera internals
double focal_length = im.cols; // Approximate focal length.
Point2d center = cv::Point2d(im.cols/2,im.rows/2);
cv::Mat camera_matrix = (cv::Mat_<double>(3,3) << focal_length, 0, center.x, 0 , focal_length, center.y, 0, 0, 1);
cv::Mat dist_coeffs = cv::Mat::zeros(4,1,cv::DataType<double>::type); // Assuming no lens distortion
cout << "Camera Matrix " << endl << camera_matrix << endl ;
// Output rotation and translation
cv::Mat rotation_vector; // Rotation in axis-angle form
cv::Mat translation_vector;
// Solve for pose
cv::solvePnP(model_points, image_points, camera_matrix, dist_coeffs, rotation_vector, translation_vector);
// Project a 3D point (0, 0, 1000.0) onto the image plane.
// We use this to draw a line sticking out of the nose
vector<Point3d> nose_end_point3D;
vector<Point2d> nose_end_point2D;
nose_end_point3D.push_back(Point3d(0,0,1000.0));
projectPoints(nose_end_point3D, rotation_vector, translation_vector, camera_matrix, dist_coeffs, nose_end_point2D);
for(int i=0; i < image_points.size(); i++)
{
circle(im, image_points[i], 3, Scalar(0,0,255), -1);
}
cv::line(im,image_points[0], nose_end_point2D[0], cv::Scalar(255,0,0), 2);
cout << "Rotation Vector " << endl << rotation_vector << endl;
cout << "Translation Vector" << endl << translation_vector << endl;
cout << nose_end_point2D << endl;
// Display image.
cv::imshow("Output", im);
cv::waitKey(0);
}旋转矩阵转换为欧拉角:
参考自:https://blog.csdn.net/zzyy0929/article/details/78323363
Yaw:摇头 左正右负
Pitch:点头 上负下正
Roll:摆头(歪头)左负 右正
static cv::Vec3d RotationMatrix2Euler(const cv::Matx33d& rotation_matrix)
{
double q0 = sqrt(1 + rotation_matrix(0, 0) + rotation_matrix(1, 1) + rotation_matrix(2, 2)) / 2.0;
double q1 = (rotation_matrix(2, 1) - rotation_matrix(1, 2)) / (4.0*q0);
double q2 = (rotation_matrix(0, 2) - rotation_matrix(2, 0)) / (4.0*q0);
double q3 = (rotation_matrix(1, 0) - rotation_matrix(0, 1)) / (4.0*q0);
double t1 = 2.0 * (q0*q2 + q1*q3);
double yaw = asin(2.0 * (q0*q2 + q1*q3));
double pitch = atan2(2.0 * (q0*q1 - q2*q3), q0*q0 - q1*q1 - q2*q2 + q3*q3);
double roll = atan2(2.0 * (q0*q3 - q1*q2), q0*q0 + q1*q1 - q2*q2 - q3*q3);
return cv::Vec3d(pitch, yaw, roll);
}python
#!/usr/bin/env python
import cv2
import numpy as np
# Read Image
im = cv2.imread("headPose.jpg");
size = im.shape
#2D image points. If you change the image, you need to change vector
image_points = np.array([
(359, 391), # Nose tip
(399, 561), # Chin
(337, 297), # Left eye left corner
(513, 301), # Right eye right corne
(345, 465), # Left Mouth corner
(453, 469) # Right mouth corner
], dtype="double")
# 3D model points.
model_points = np.array([
(0.0, 0.0, 0.0), # Nose tip
(0.0, -330.0, -65.0), # Chin
(-225.0, 170.0, -135.0), # Left eye left corner
(225.0, 170.0, -135.0), # Right eye right corne
(-150.0, -150.0, -125.0), # Left Mouth corner
(150.0, -150.0, -125.0) # Right mouth corner
])
# Camera internals
focal_length = size[1]
center = (size[1]/2, size[0]/2)
camera_matrix = np.array(
[[focal_length, 0, center[0]],
[0, focal_length, center[1]],
[0, 0, 1]], dtype = "double"
)
print "Camera Matrix :\n {0}".format(camera_matrix)
dist_coeffs = np.zeros((4,1)) # Assuming no lens distortion
(success, rotation_vector, translation_vector) = cv2.solvePnP(model_points, image_points, camera_matrix, dist_coeffs, flags=cv2.CV_ITERATIVE)
print "Rotation Vector:\n {0}".format(rotation_vector)
print "Translation Vector:\n {0}".format(translation_vector)
# Project a 3D point (0, 0, 1000.0) onto the image plane.
# We use this to draw a line sticking out of the nose
(nose_end_point2D, jacobian) = cv2.projectPoints(np.array([(0.0, 0.0, 1000.0)]), rotation_vector, translation_vector, camera_matrix, dist_coeffs)
for p in image_points:
cv2.circle(im, (int(p[0]), int(p[1])), 3, (0,0,255), -1)
p1 = ( int(image_points[0][0]), int(image_points[0][1]))
p2 = ( int(nose_end_point2D[0][0][0]), int(nose_end_point2D[0][0][1]))
cv2.line(im, p1, p2, (255,0,0), 2)
# Display image
cv2.imshow("Output", im)
cv2.waitKey(0)另一种实现
class PnpHeadPoseEstimator:
""" Head pose estimation class which uses the OpenCV PnP algorithm.
It finds Roll, Pitch and Yaw of the head given a figure as input.
It uses the PnP algorithm and it requires the dlib library
"""
def __init__(self, cam_w, cam_h, dlib_shape_predictor_file_path):
""" Init the class
@param cam_w the camera width. If you are using a 640x480 resolution it is 640
@param cam_h the camera height. If you are using a 640x480 resolution it is 480
@dlib_shape_predictor_file_path path to the dlib file for shape prediction (look in: deepgaze/etc/dlib/shape_predictor_68_face_landmarks.dat)
"""
if(IS_DLIB_INSTALLED == False): raise ValueError('[DEEPGAZE] PnpHeadPoseEstimator: the dlib libray is not installed. Please install dlib if you want to use the PnpHeadPoseEstimator class.')
if(os.path.isfile(dlib_shape_predictor_file_path)==False): raise ValueError('[DEEPGAZE] PnpHeadPoseEstimator: the files specified do not exist.')
#Defining the camera matrix.
#To have better result it is necessary to find the focal
# lenght of the camera. fx/fy are the focal lengths (in pixels)
# and cx/cy are the optical centres. These values can be obtained
# roughly by approximation, for example in a 640x480 camera:
# cx = 640/2 = 320
# cy = 480/2 = 240
# fx = fy = cx/tan(60/2 * pi / 180) = 554.26
c_x = cam_w / 2
c_y = cam_h / 2
f_x = c_x / np.tan(60/2 * np.pi / 180)
f_y = f_x
#Estimated camera matrix values.
self.camera_matrix = np.float32([[f_x, 0.0, c_x],
[0.0, f_y, c_y],
[0.0, 0.0, 1.0] ])
#These are the camera matrix values estimated on my webcam with
# the calibration code (see: src/calibration):
#camera_matrix = np.float32([[602.10618226, 0.0, 320.27333589],
#[ 0.0, 603.55869786, 229.7537026],
#[ 0.0, 0.0, 1.0] ])
#Distortion coefficients
self.camera_distortion = np.float32([0.0, 0.0, 0.0, 0.0, 0.0])
#Distortion coefficients estimated by calibration in my webcam
#camera_distortion = np.float32([ 0.06232237, -0.41559805, 0.00125389, -0.00402566, 0.04879263])
if(DEBUG==True): print("[DEEPGAZE] PnpHeadPoseEstimator: estimated camera matrix: \n" + str(self.camera_matrix) + "\n")
#Declaring the dlib shape predictor object
self._shape_predictor = dlib.shape_predictor(dlib_shape_predictor_file_path)
def _return_landmarks(self, inputImg, roiX, roiY, roiW, roiH, points_to_return=range(0,68)):
""" Return the the roll pitch and yaw angles associated with the input image.
@param image It is a colour image. It must be >= 64 pixel.
@param radians When True it returns the angle in radians, otherwise in degrees.
"""
#Creating a dlib rectangle and finding the landmarks
dlib_rectangle = dlib.rectangle(left=int(roiX), top=int(roiY), right=int(roiW), bottom=int(roiH))
dlib_landmarks = self._shape_predictor(inputImg, dlib_rectangle)
#It selects only the landmarks that
#have been indicated in the input parameter "points_to_return".
#It can be used in solvePnP() to estimate the 3D pose.
landmarks = np.zeros((len(points_to_return),2), dtype=np.float32)
counter = 0
for point in points_to_return:
landmarks[counter] = [dlib_landmarks.parts()[point].x, dlib_landmarks.parts()[point].y]
counter += 1
return landmarks
def return_roll_pitch_yaw(self, image, radians=False):
""" Return the the roll pitch and yaw angles associated with the input image.
@param image It is a colour image. It must be >= 64 pixel.
@param radians When True it returns the angle in radians, otherwise in degrees.
"""
#The dlib shape predictor returns 68 points, we are interested only in a few of those
TRACKED_POINTS = (0, 4, 8, 12, 16, 17, 26, 27, 30, 33, 36, 39, 42, 45, 62)
#Antropometric constant values of the human head.
#Check the wikipedia EN page and:
#"Head-and-Face Anthropometric Survey of U.S. Respirator Users"
#
#X-Y-Z with X pointing forward and Y on the left and Z up.
#The X-Y-Z coordinates used are like the standard
# coordinates of ROS (robotic operative system)
#OpenCV uses the reference usually used in computer vision:
#X points to the right, Y down, Z to the front
#
#The Male mean interpupillary distance is 64.7 mm (https://en.wikipedia.org/wiki/Interpupillary_distance)
#
P3D_RIGHT_SIDE = np.float32([-100.0, -77.5, -5.0]) #0
P3D_GONION_RIGHT = np.float32([-110.0, -77.5, -85.0]) #4
P3D_MENTON = np.float32([0.0, 0.0, -122.7]) #8
P3D_GONION_LEFT = np.float32([-110.0, 77.5, -85.0]) #12
P3D_LEFT_SIDE = np.float32([-100.0, 77.5, -5.0]) #16
P3D_FRONTAL_BREADTH_RIGHT = np.float32([-20.0, -56.1, 10.0]) #17
P3D_FRONTAL_BREADTH_LEFT = np.float32([-20.0, 56.1, 10.0]) #26
P3D_SELLION = np.float32([0.0, 0.0, 0.0]) #27 This is the world origin
P3D_NOSE = np.float32([21.1, 0.0, -48.0]) #30
P3D_SUB_NOSE = np.float32([5.0, 0.0, -52.0]) #33
P3D_RIGHT_EYE = np.float32([-20.0, -32.35,-5.0]) #36
P3D_RIGHT_TEAR = np.float32([-10.0, -20.25,-5.0]) #39
P3D_LEFT_TEAR = np.float32([-10.0, 20.25,-5.0]) #42
P3D_LEFT_EYE = np.float32([-20.0, 32.35,-5.0]) #45
#P3D_LIP_RIGHT = np.float32([-20.0, 65.5,-5.0]) #48
#P3D_LIP_LEFT = np.float32([-20.0, 65.5,-5.0]) #54
P3D_STOMION = np.float32([10.0, 0.0, -75.0]) #62
#This matrix contains the 3D points of the
# 11 landmarks we want to find. It has been
# obtained from antrophometric measurement
# of the human head.
landmarks_3D = np.float32([P3D_RIGHT_SIDE,
P3D_GONION_RIGHT,
P3D_MENTON,
P3D_GONION_LEFT,
P3D_LEFT_SIDE,
P3D_FRONTAL_BREADTH_RIGHT,
P3D_FRONTAL_BREADTH_LEFT,
P3D_SELLION,
P3D_NOSE,
P3D_SUB_NOSE,
P3D_RIGHT_EYE,
P3D_RIGHT_TEAR,
P3D_LEFT_TEAR,
P3D_LEFT_EYE,
P3D_STOMION])
#Return the 2D position of our landmarks
img_h, img_w, img_d = image.shape
landmarks_2D = self._return_landmarks(inputImg=image, roiX=0, roiY=img_w, roiW=img_w, roiH=img_h, points_to_return=TRACKED_POINTS)
#Print som red dots on the image
#for point in landmarks_2D:
#cv2.circle(frame,( point[0], point[1] ), 2, (0,0,255), -1)
#Applying the PnP solver to find the 3D pose
#of the head from the 2D position of the
#landmarks.
#retval - bool
#rvec - Output rotation vector that, together with tvec, brings
#points from the world coordinate system to the camera coordinate system.
#tvec - Output translation vector. It is the position of the world origin (SELLION) in camera co-ords
retval, rvec, tvec = cv2.solvePnP(landmarks_3D,
landmarks_2D,
self.camera_matrix,
self.camera_distortion)
#Get as input the rotational vector
#Return a rotational matrix
rmat, _ = cv2.Rodrigues(rvec)
#euler_angles contain (pitch, yaw, roll)
#euler_angles = cv.DecomposeProjectionMatrix(projMatrix=rmat, cameraMatrix=camera_matrix, rotMatrix, transVect, rotMatrX=None, rotMatrY=None, rotMatrZ=None)
head_pose = [ rmat[0,0], rmat[0,1], rmat[0,2], tvec[0],
rmat[1,0], rmat[1,1], rmat[1,2], tvec[1],
rmat[2,0], rmat[2,1], rmat[2,2], tvec[2],
0.0, 0.0, 0.0, 1.0 ]
#print(head_pose) #TODO remove this line
return self.rotationMatrixToEulerAngles(rmat)
# Calculates rotation matrix to euler angles
# The result is the same as MATLAB except the order
# of the euler angles ( x and z are swapped ).
def rotationMatrixToEulerAngles(self, R) :
#assert(isRotationMatrix(R))
#To prevent the Gimbal Lock it is possible to use
#a threshold of 1e-6 for discrimination
sy = math.sqrt(R[0,0] * R[0,0] + R[1,0] * R[1,0])
singular = sy < 1e-6
if not singular :
x = math.atan2(R[2,1] , R[2,2])
y = math.atan2(-R[2,0], sy)
z = math.atan2(R[1,0], R[0,0])
else :
x = math.atan2(-R[1,2], R[1,1])
y = math.atan2(-R[2,0], sy)
z = 0
return np.array([x, y, z])和上面那版代码主要思想相同,不同点有:
- fx,fy计算方式不同;
- 使用的二维特征点不同;
- 增加了根据旋转矩阵R计算欧拉角的实现。








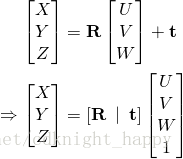
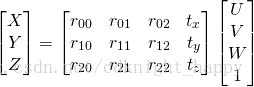
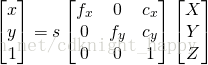
















 2290
2290











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








