要以这个开头:
我爱你反演!❤
以下内容只是为了给自己看
%%%VFleaKing
下面进入正题:
什么是反演

二项式反演
ppt一开始给了一道题目:

这是个很简单的容斥问题:
F
(
n
)
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
(
n
−
k
)
!
F(n)=\sum_{k=0}^{n}(-1)^{k}\tbinom{n}{k}(n-k)!
F(n)=k=0∑n(−1)k(kn)(n−k)!
原文用了和通俗易懂的说法和图来解释这个容斥,风趣幽默,拉近与读者的距离
怎么变成评论文学价值了?


原本用了一些篇幅来写为什么这个容斥系数要么是-1要么是1,这是我从来没有想过的。(菜鸡的微笑)
其实思考一下可以发现,(算了搬原文)

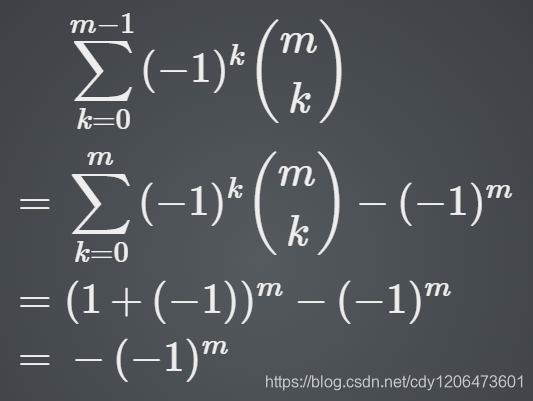
刺不刺激,惊不惊喜!
(菜鸡捂嘴表示惊叹)
这个大哥(叫一声大哥)让我弄懂了出生到现在没有想过的东西!!!!
从另一个角度看上面式子左半边是!
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
=
[
n
=
0
]
\sum_{k=0}^{n}(-1)^k\tbinom{n}{k}=[n=0]
k=0∑n(−1)k(kn)=[n=0]
然后用反演思想看一下~
我们设
F
(
n
)
F(n)
F(n)表示n个人随便站的方案数
G
(
n
)
G(n)
G(n)表示n个人没有一个人站对的方案数
那么 F ( n ) = ∑ k = 0 n ( n k ) G ( n ) F(n)=\sum_{k=0}^{n}\tbinom{n}{k}G(n) F(n)=k=0∑n(kn)G(n)
注意注意!然后要开始反演了!!!!
原文称为"魔术":
简单易懂的废话:
G
(
n
)
=
∑
m
=
0
n
[
n
−
m
=
0
]
(
n
m
)
G
(
m
)
G(n)=\sum_{m=0}^{n}[n-m=0]\tbinom{n}{m}G(m)
G(n)=m=0∑n[n−m=0](mn)G(m)
一开始我还一脸懵逼,后来发现这个式子等于
G
(
n
)
=
G
(
m
)
[
m
=
n
]
G(n)=G(m)[m=n]
G(n)=G(m)[m=n]
然后上面那个东西用到啦!!
复习一下:
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
=
[
n
=
0
]
\sum_{k=0}^{n}(-1)^k\tbinom{n}{k}=[n=0]
k=0∑n(−1)k(kn)=[n=0]
所以代入:
G
(
n
)
=
∑
m
=
0
n
∑
k
=
0
n
−
m
(
−
1
)
k
(
n
−
m
k
)
(
n
m
)
G
(
m
)
G(n)=\sum_{m=0}^{n}\sum_{k=0}^{n-m}(-1)^k\tbinom{n-m}{k}\tbinom{n}{m}G(m)
G(n)=m=0∑nk=0∑n−m(−1)k(kn−m)(mn)G(m)
我一直不知道这个东西
(
n
−
m
k
)
(
n
m
)
\tbinom{n-m}{k}\tbinom{n}{m}
(kn−m)(mn)怎么转换,今天懂了!
等于在n里面选m个数然后在余下的里面再选k个数。
所以等价于:
(
n
k
)
(
n
−
k
m
)
\tbinom{n}{k}\tbinom{n-k}{m}
(kn)(mn−k)
所以原式=
G
(
n
)
=
∑
m
=
0
n
∑
k
=
0
n
−
m
(
−
1
)
k
(
n
k
)
(
n
−
k
m
)
G
(
m
)
G(n)=\sum_{m=0}^{n}\sum_{k=0}^{n-m}(-1)^k\tbinom{n}{k}\tbinom{n-k}{m}G(m)
G(n)=m=0∑nk=0∑n−m(−1)k(kn)(mn−k)G(m)
下面他的操作有点迷: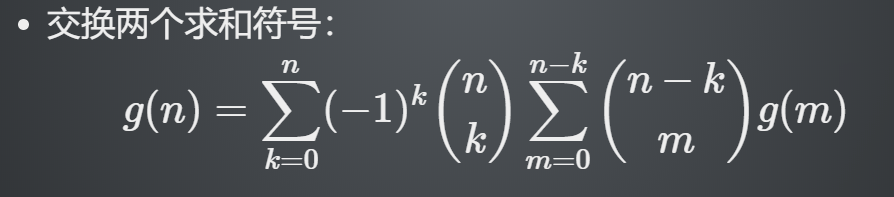
这东西我愣是没有看懂,后来发现。
假设
k
=
n
−
m
−
p
(
0
≤
p
≤
n
−
m
)
k=n-m-p(0\leq p\leq n-m)
k=n−m−p(0≤p≤n−m)
那么
m
=
n
−
k
−
p
m=n-k-p
m=n−k−p
所以枚举p过程中发现其实上面那条式子就是成立的了。
枚举的每一个k都有所有确定的m=n-k-p与之对应
综上所述,上述式子正确!
G ( n ) = ∑ k = 0 n ( − 1 ) k ( n k ) ∑ m = 0 n − k ( n − k m ) G ( m ) G(n)=\sum_{k=0}^{n}(-1)^k\tbinom{n}{k}\sum_{m=0}^{n-k}\tbinom{n-k}{m}G(m) G(n)=k=0∑n(−1)k(kn)m=0∑n−k(mn−k)G(m)
”注意最右边的那个小朋友!其实就是 F F F!“
对比上面F的式子:
F
(
n
)
=
∑
k
=
0
n
(
n
k
)
G
(
n
)
F(n)=\sum_{k=0}^{n}\tbinom{n}{k}G(n)
F(n)=k=0∑n(kn)G(n)
发现:
G
(
n
)
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
F
(
n
−
k
)
G(n)=\sum_{k=0}^{n}(-1)^k\tbinom{n}{k}F(n-k)
G(n)=k=0∑n(−1)k(kn)F(n−k)
把下表搞好看点就是
G
(
n
)
=
∑
k
=
0
n
(
−
1
)
n
−
k
(
n
k
)
F
(
k
)
G(n)=\sum_{k=0}^{n}(-1)^{n-k}\tbinom{n}{k}F(k)
G(n)=k=0∑n(−1)n−k(kn)F(k)
这就是著名的二项式反演!
F
(
n
)
=
∑
k
=
0
n
(
n
k
)
G
(
n
)
F(n)=\sum_{k=0}^{n}\tbinom{n}{k}G(n)
F(n)=k=0∑n(kn)G(n)
G
(
n
)
=
∑
k
=
0
n
(
−
1
)
n
−
k
(
n
k
)
F
(
k
)
G(n)=\sum_{k=0}^{n}(-1)^{n-k}\tbinom{n}{k}F(k)
G(n)=k=0∑n(−1)n−k(kn)F(k)
至此,二项式反演告一段落
看到这里我作为菜鸡看得满头大汗!
好的大哥,您成功激起了我对反演的兴趣呢!
莫比乌斯反演
原文叫做:
又是一道题目出来:

还是设!
设
F
(
n
)
F(n)
F(n) 表示长度为
n
n
n 的字符串的个数。
设
G
(
n
)
G(n)
G(n) 表示长度为
n
n
n 的且周期为
n
n
n 的字符串的个数。
F ( n ) = ∑ d ∣ n G ( d ) F(n)=\sum_{d|n}G(d) F(n)=d∣n∑G(d)
这就是典型的莫某某反演的形式
然后?
发现我们刚才是怎么搞出二项式反演的?
用一句废话然后带进去不是吗?
在这里我们同样定义:
设
μ
(
n
)
\mu(n)
μ(n)满足
∑
d
∣
n
μ
(
d
)
=
[
n
=
1
]
\sum_{d|n}\mu(d)=[n=1]
d∣n∑μ(d)=[n=1]
为什么这次是1?
因为刚刚判断相等是用减法,这次我们用除法,相同的数相除当然是1咯!
又是一句废话开始魔术~
G
(
n
)
=
∑
m
∣
n
[
n
m
=
1
]
G
(
m
)
G(n)=\sum_{m|n}[\frac{n}{m}=1]G(m)
G(n)=m∣n∑[mn=1]G(m)
然后顺理成章地代入:
G
(
n
)
=
∑
m
∣
n
∑
d
∣
n
m
μ
(
d
)
G
(
m
)
G(n)=\sum_{m|n}\sum_{d|\frac{n}{m}}\mu(d)G(m)
G(n)=m∣n∑d∣mn∑μ(d)G(m)
再用刚刚的方法,用d把m表示出来,就是
m
∣
n
d
m|\frac{n}{d}
m∣dn
然后?顺理成章:
G
(
n
)
=
∑
d
∣
n
μ
(
d
)
∑
m
∣
n
d
G
(
m
)
G(n)=\sum_{d|n}\mu(d)\sum_{m|\frac{n}{d}}G(m)
G(n)=d∣n∑μ(d)m∣dn∑G(m)
”
F
F
F君好久不见~“
G
(
n
)
=
∑
d
∣
n
μ
(
d
)
F
(
n
d
)
G(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})
G(n)=d∣n∑μ(d)F(dn)
换一下:
G
(
n
)
=
∑
d
∣
n
μ
(
n
d
)
F
(
d
)
G(n)=\sum_{d|n}\mu(\frac{n}{d})F(d)
G(n)=d∣n∑μ(dn)F(d)
这样就得到了莫比乌斯反演了~
F ( n ) = ∑ d ∣ n G ( d ) F(n)=\sum_{d|n}G(d) F(n)=d∣n∑G(d) G ( n ) = ∑ d ∣ n μ ( n d ) F ( d ) G(n)=\sum_{d|n}\mu(\frac{n}{d})F(d) G(n)=d∣n∑μ(dn)F(d)
后面又一道题目,我是跪着看完的


























 1222
1222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








