非线性模型预测控制车辆自动驾驶控制【附CarSim/Simulink】

✅博主简介：本人擅长建模仿真、程序设计、论文写作与指导，项目与课题经验交流。项目合作可私信或扫描文章底部二维码。

---

运动控制算法需适应更广泛的工况范围。然而，现有的非线性模型预测控制（NMPC）算法面临着一些挑战，特别是在车辆运动控制模型的设计上，单一的模型往往适用范围窄，无法覆盖全速工况。为此，本文提出了一种整合车辆运动学与动力学的综合模型（Integrated Kinematic and Dynamic Model，IKD），旨在扩大单一车辆运动控制模型的适用工况范围。

IKD模型的提出与分析

IKD模型通过结合车辆的运动学特性和动力学特性来进行设计，旨在提供更全面的运动描述。该模型不仅考虑了车辆的基本运动学特性，例如位置、速度和加速度，还整合了动力学因素，如质心位置、重心高度和转向特性等。在模型精度和复杂度之间进行了权衡，重点分析了横向和纵向动力学之间的耦合关系。针对动力学耦合较弱的部分，我们对模型进行了简化，从而提高了计算效率。

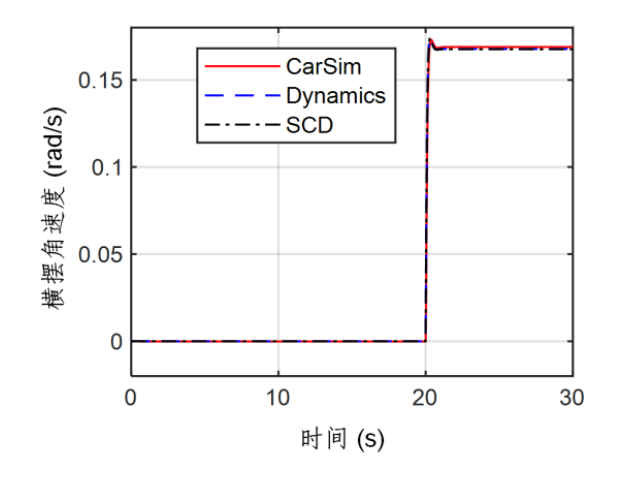
在CarSim和Simulink的联合仿真平台上，我们进行了横向和纵向运动特性试验。通过对比IKD模型、传统的运动学模型和动力学模型，验证了IKD模型在高低速工况下均表现出较好的模型精度。实验结果显示，在不同速度和不同操控条件下，IKD模型能够有效捕捉车辆的动态特性，展现出更好的控制性能。

NMPC算法的计算效率与控制精度

在自动驾驶系统中，NMPC算法的计算效率和控制精度至关重要。在离散求解NMPC运动控制问题时，车辆模型方程的刚性特征会对计算效率造成影响。当模型表现出刚性时，传统的离散方法需要使用较小的离散时间步长，以确保求解的精度和数值计算的稳定性。然而，较小的时间步长会导致计算效率降低。

为此，我们提出了一种基于有限单元正交配置（Orthogonal Collocation on Finite Elements，OCFE）离散的NMPC运动控制算法。这种方法相比传统的欧拉离散法和四阶龙格-库塔法，能够在保证数值稳定性的前提下，提高NMPC求解的计算效率。通过CarSim和Simulink的联合仿真对比，验证了基于OCFE离散的NMPC控制算法在刚性方程情况下的优越性。

此外，当车辆模型为非刚性方程时，OCFE离散方法同样展现出更高的精度。仿真结果表明，该方法有效解决了因模型刚性导致的计算低效问题，同时提高了控制精度，为自动驾驶系统的实时控制提供了更可靠的技术支持。

极限工况下的控制挑战

在高速转向和低附着路面等极限工况下，车辆模型的非线性特性加剧，NMPC算法的实时求解负担也随之增加。这不仅影响了控制系统的响应速度，还可能导致车辆失去稳定性，进而造成轨迹跟踪的失败。因此，必须设计一种综合考虑控制精度、实时性和车辆稳定性的控制算法。

针对这一挑战，本文研究设计了轨迹跟踪控制算法和稳定性控制算法。在极限工况下，为了平衡轨迹跟踪控制的精度和实时性，我们利用NMPC的滚动优化特性，提出了一种级联离散方法。此外，为特定的高速行驶场景，设计了一种NMPC预测时域扩展策略，以提高控制的适应性和精度。

在稳定性控制方面，我们引入了主动后轮转向技术，以防止车辆质心侧偏角的过度增大。这一措施有助于在极限工况下保持车辆的稳定性。此外，通过实时估计轮胎侧向力，我们可以对侧偏刚度进行校正，从而增强控制算法的鲁棒性。

通过在CarSim和Simulink的联合仿真中验证，所提出的运动控制算法能够在高速转向和低附着路面等极限工况下，保持良好的车辆稳定性，同时实现轨迹跟踪精度与控制实时性的良好平衡。实验结果显示，该控制策略在应对动态环境和复杂工况时，表现出优越的适应能力和稳定性。

% Nonlinear Model Predictive Control for Autonomous Vehicle

% Parameters initialization
dt = 0.1; % Time step
T = 20; % Total simulation time in seconds
N = T/dt; % Number of time steps

% Vehicle model parameters
L = 2.5; % Wheelbase
mass = 1500; % Vehicle mass in kg
Iz = 2500; % Yaw moment of inertia
Cf = 19000; % Cornering stiffness front
Cr = 19000; % Cornering stiffness rear

% State vectors initialization
x = zeros(N, 1); % X position
y = zeros(N, 1); % Y position
theta = zeros(N, 1); % Orientation angle
vx = zeros(N, 1); % Velocity in x
vy = zeros(N, 1); % Velocity in y
delta = zeros(N, 1); % Steering angle

% NMPC parameters
Q = diag([1, 1, 1, 0.1]); % State cost matrix
R = diag([0.1]); % Control cost matrix

% Simulation loop
for k = 1:N-1
    % Define the state vector
    state = [x(k); y(k); theta(k); vx(k); vy(k)];
    
    % Define the desired trajectory (straight line for simplicity)
    desired_state = [x(k) + 5; y(k); 0; 10; 0]; % Next point
    
    % NMPC optimization problem (placeholder for the optimization logic)
    % Here you would set up your optimization problem based on the state
    % and desired trajectory, solve it, and extract the control inputs.
    
    % Example control input update (placeholder)
    control_input = -inv(R) * (state - desired_state); % Simple feedback for demo
    
    % Update state based on control input (basic bicycle model)
    vx(k+1) = vx(k) + control_input(1) * dt; % Update velocity
    delta(k+1) = control_input(2); % Update steering angle
    x(k+1) = x(k) + vx(k) * cos(theta(k)) * dt;
    y(k+1) = y(k) + vx(k) * sin(theta(k)) * dt;
    theta(k+1) = theta(k) + (vx(k) / L) * tan(delta(k)) * dt; % Update orientation
end

% Plot the results
figure;
subplot(3, 1, 1);
plot(x, y);
xlabel('X Position (m)');
ylabel('Y Position (m)');
title('Vehicle Path Tracking');

subplot(3, 1, 2);
plot(0:dt:T-dt, vx);
xlabel('Time (s)');
ylabel('Velocity (m/s)');
title('Vehicle Velocity');

subplot(3, 1, 3);
plot(0:dt:T-dt, delta);
xlabel('Time (s)');
ylabel('Steering Angle (rad)');
title('Steering Angle Control');