
✅ 博主简介:擅长数据搜集与处理、建模仿真、程序设计、仿真代码、论文写作与指导,毕业论文、期刊论文经验交流。
✅ 具体问题可以私信或扫描文章底部二维码。
-
自动驾驶系统的背景与发展 随着城市轨道交通的快速发展,列车的运行速度和行车密度不断提升,传统的人工驾驶模式已无法满足现代列车的运行需求。在这种背景下,自动驾驶系统(ATO)应运而生。ATO系统通过计算机、传感器和通信设备的协同工作,能够有效控制列车的运行速度、启动和停车等操作。这一系统的引入不仅提高了列车的运行效率和安全性,还显著提升了乘客的舒适度。此外,ATO系统能够减少驾驶员的工作强度,降低因人为因素导致的事故风险,使驾驶员能够更专注于列车的监控和应急处理。
-
列车动力学模型的建立与辨识 在对列车运行模型进行动力学分析时,首先需要建立列车的单质点模型。通过应用最小二乘法,可以在牵引工况下辨识出城轨列车的动力学模型。研究表明,二阶模型的均方差为 1.5215×10−51.5215×10−5,小于标准值 10−410−4,这表明模型的准确性较高。通过这一模型,可以计算出城轨列车的传递函数,为后续的控制策略提供了理论基础。
-
控制优化策略的应用 在控制优化方面,遗传算法(GA)和模糊控制算法被应用于PID参数的整定。通过GA-PID速度控制器和模糊PID速度控制器,可以有效追踪列车的目标运行曲线。对比分析显示,模糊PID速度控制器在运行时间误差上比GA-PID控制器小0.02秒,停车距离的误差比GA-PID速度控制器小10厘米,且在两站之间的能耗比GA-PID速度控制器减少了约4%。仿真结果表明,模糊PID速度控制器在追踪列车目标曲线的精度和乘客的舒适性方面均优于GA-PID速度控制器。
clear;
close all;
% 参数初始化
mass = 20000; % 列车质量 (kg)
friction = 0.1; % 摩擦系数
time = 0:0.1:100; % 时间范围 (s)
input_signal = sin(0.1*time); % 输入信号 (模拟牵引力)
% 动力学模型
acceleration = (input_signal - friction * mass) / mass; % 加速度计算
velocity = cumtrapz(time, acceleration); % 速度计算
position = cumtrapz(time, velocity); % 位置计算
% 绘制结果
figure;
subplot(3,1,1);
plot(time, acceleration);
title('Acceleration');
xlabel('Time (s)');
ylabel('Acceleration (m/s^2)');
subplot(3,1,2);
plot(time, velocity);
title('Velocity');
xlabel('Time (s)');
ylabel('Velocity (m/s)');
subplot(3,1,3);
plot(time, position);
title('Position');
xlabel('Time (s)');
ylabel('Position (m)');
% PID控制器参数整定
Kp = 1; % 比例增益
Ki = 0.1; % 积分增益
Kd = 0.01; % 微分增益
pid_controller = pid(Kp, Ki, Kd);
% 仿真控制
sim_time = 50; % 仿真时间
sim('pid_control_model', sim_time); % 运行仿真模型
% 结果分析
disp('仿真结束,结果已输出。');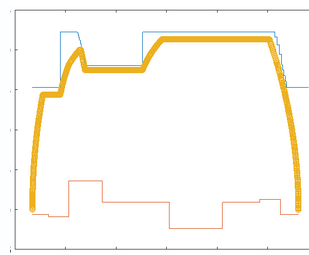

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










