最优化方法及其Matlab程序设计

2chen_

于 2024-09-14 18:24:05 发布

阅读量972

点赞数 26

文章标签：算法机器学习人工智能

本文链接：https://blog.csdn.net/chen030209/article/details/141465523

版权

第 1 章最优化理论基础

1.1 最优化问题的数学模型

人们通常按照可行集的性质对最优化问题进行一个大致的分类.

(1) 线性规划和非线性规划：可行集是有限维空间中的一个子集.

(2) 组合优化或网络规划：可行集中的元素是有限的.

(3) 动态规划：可行集是一个依赖于时间的决策序列.

(4) 最优控制：可行集是无穷维空间中的一个连续子集.

非线性规划的数学模型为

1.2 向量和矩阵函数

1.3 函数的可微性与展开

f(x) 在 x 处的二阶导数或 Hesse 矩阵

若 Hesse 矩阵的各个分量函数都连续，则称 f(x) 在 x 二阶连续可微.

Hesse 矩阵是对称阵

1.4 凸集与凸函数

设集合 $D\subset \mathbb{R}^n$ ，称集合 D 为凸集，是指对任意的 $x,y\in D$ 及任意的实数 $\lambda \in [0,1]$ ，都有 $\lambda x+(1-\lambda)y\in D$

设 0,2,5是凸集，a 是一实数，那么

(1) $\alpha D=\{y|y=\alpha x,x\in D\}$ 是凸集；

(2) 交集 $D_1 \cap D_2$ 是凸集；

(3) 和集 $D_1 + D_2 =\{z|z=x+y,x\in D_1,y\in D_2 \}$ 也是凸集

设函数 $f:D\subset \mathbb{R}^n\rightarrow \mathbb{R}$ ，其中 D 为凸集.

(1) 称 f 为 D 上的凸函数，是指对任意的 $x,y\in D$ 及任意的实数 $\lambda \in [0,1]$ ，都有

充要条件是

(2) 称 f 为 D 上的严格凸函数，是指对任意的 $x,y\in D,x\neq y$ 及任意的实数 $\lambda \in [0,1]$ ，都有

即中间低两边高

充要条件是

(3) 称 f 为 D 上的一致凸函数，是指存在常数 $\gamma >0$ ，使得对任意的 $x,y\in D$ 及任意的实数 $\lambda \in [0,1]$ ，都有

充要条件是存在常数 c > 0，使得对任意的 $x^*,x\in D$ ，成立

设 n 元实函数 f 在凸集 D 上是二阶连续可微的，若对一切 $h\in \mathbb{R}$ 有 $h^T\triangledown ^2f(x)h \ge 0$ ，则称 $\triangledown ^2f$ 在点 x 处为半正定的。

若对一切 $0 \neq h\in \mathbb{R}^n$ 有 $h^T\triangledown ^2f(x)h > 0$ ，则称 $\triangledown ^2f$ 在点 x 处为正定的

进一步，若存在常数 c > 0，使得对任意的 $h\in \mathbb{R}^n$ ， $x\in D$ 有 $h^T\triangledown ^2f(x)\ge c\left \| h \right \|^2$ ，则称 $\triangledown ^2f$ 在 D 上为一致正定的

(1) f 在 D 上是凸的充要条件是 $\triangledown ^2f$ 对一切 $x\in D$ 为半正定；

(2) f 在 D 上是严格凸的充分条件是 $\triangledown ^2f$ 对一切 $x\in D$ 为正定；

(3) f 在 D 上是一致凸的充要条件是 $\triangledown ^2f$ 对一切 $x\in D$ 为一致正定.

注意： $\triangledown ^2f$ 正定是 f 严格凸的充分条件而非必要条件.

1.5 无约束问题的最优性条件

1.6 无约束优化问题的算法框架

无约束问题的一般算法框架

步 0 给定初始化参数及初始迭代点 $x_0$ ，置 k := 0.

步 1 若 $x_k$ 满足某种终止准则，停止迭代，以 $x_k$ 作为近似极小点.

步 2 通过求解 $x_k$ 处的某个子问题确定下降方向 $d_k$ .

步 3 通过某种搜索方式确定步长因子 $\alpha _k$ ，使得 $f(x_k+\alpha _kd_k)<f(x_k)$

步 4 令 $x_{k+1}:=x_k+\alpha _kd_k,k:=k+1$ ，转步 1

为了方便起见，通常称 $s_k=\alpha _kd_k$ 为第 k 次迭代的位移。

可以看出，不同的位移 (不同的搜索方向及步长因子) 即产生了不同的迭代算法。

为了保证算法的收敛性，一般要求搜索方向为所谓的下降方向

若存在 $\bar{\alpha}>0$ ，使得对任意的 $\alpha \in (0,\bar{\alpha}]$ 和 $d_k\neq 0$ 有

则称 $d_k$ 为 $f(x)$ 在 $x_k$ 处的一个下降方向.

设函数 $f:D\subset \mathbb{R} ^n \rightarrow \mathbb{R}$ 在开集 D 上一阶连续可微，则 $d_k$ 为 $f(x)$ 在 $x_k$ 处的一个下降方向的充要条件是

第 2 章线搜索技术

通过某种搜索方式确定步长因子 $\alpha$ ，使得

这实际上是 ( n 个变量的) 目标函数 f(x) 在一个规定的方向上移动所形成的单变量优化问题，也就是所谓的“线搜索”或“一维搜索”技术，令

这样，搜索式等价于求步长 $\alpha_k$ ，使得

线搜索有精确线搜索和非精确线搜索之分，所谓精确线搜索，是指求 $\alpha_k$ ，使得目标函数 f 沿方向 $d_k$ 达到极小，即

或

若 f(x) 是连续可微的，那么由精确线搜索得到的步长因子 $\alpha_k$ ，具有如下性质：

所谓非精确线搜索，是指选取 $\alpha_k$ ，使得目标函数 f 得到可接受的下降量，即 $\Delta f_k=f(x_k)-f(x_k+\alpha_kd_k)>0$ 是可接受的

精确线搜索的基本思想是：首先确定包含问题最优解的搜索区间,然后采用某种插值或分割技术缩小这个区间，进行搜索求解，下面给出搜索区间的定义.

设 $\phi$ 是定义在实数集上一元实函数， $\alpha^*\in [0,+\infty)$ ，并且

若存在区间 $[a,b]\subset [0,+\infty)$ ，使得 $\alpha^*\in(a,b)$ ，则称 [a, b] 为极小化问题的搜索区间。

若 a* 使得 $\phi(\alpha)$ 在 $[a,\alpha^*]$ 上严格递减，在 $[\alpha^*,b]$ 上严格递增，则称 [a, b] 为 $\phi(\alpha)$ 的单峰区间， $\phi(\alpha)$ 为 [a, b] 上的单峰函数.

下面介绍一种确定搜索区间，并保证具有近似单峰性质的数值算法——进退法，其基本思想是从一点出发，按一定步长，试图确定函数值呈现“高-低-高”的三点，从而得到一个近似的单峰区间

进退法

步 1 选取 $\alpha _0\ge 0,h_0>0$ ，计算 $\phi _0:=\phi(\alpha _0)$ ，置 k := 0.

步 2 令 $\alpha _{k+1}=\alpha _k+h_k$ ，计算 $\phi _{k+1}:=\phi (\alpha _{k+1})$ ，若 $\phi _{k+1}<\phi _k$ ，转步 3; 否则, 转步 4.

步 3 加大步长。 $h_{k+1}:=2h_k,\alpha :=\alpha _k,\alpha _k:=\alpha _{k+1},\phi _k:=\phi _{k+1},k:=k+1$ ，转步 2.

步 4 反向搜索或输出。若 k = 0，令 $h_1:=h_0,\alpha :=\alpha _1,\alpha_1:=\alpha _0,\phi _1:=\phi _0,k:=1$ ，转步 2; 否则，停止迭代，令 $a=\min\{\alpha,\alpha _{k+1}\},b=\max\{\alpha,\alpha _{k+1}\}$ ，输出 [a, b]

2.1 精确线搜索及其Matlab实现

2.1.1 黄金分割法

步 0 确定初始搜索区间 $[a_0,b_0]$ 和容许误差 $\varepsilon >0$ 。计算初始试探点

及相应的函数值 $\phi (p_0),\phi (q_0)$ ，置 $i:=0$

步 1 若 $\phi (p_i)\le \phi (q_i)$ ；转步 2；否则，转步 3.

步 2 计算左试探点。若 $|q_i-a_i|\le \varepsilon$ ，停算，输出 $p_i$ ；否则，令

计算 $\phi (p_{i+1}),i:=i+1$ ，转步 1.

步 3 计算右试探点。若 $|b_i-p_i|\le \varepsilon$ ，停算，输出 $q_i$ ；否则，令

计算 $\phi (q_{i+1}),i:=i+1$ ，转步 1.

0.618 法程序

%function [s,phis,k,G,E]=golds(phi,a,b,delta,epsilon)
%榆入：phi是目标函数，a, b 是搜索区间的两个端点
% delta, epsilon分别是自变量和函数值的容许误差
%输出：s, phis分别是近似极小点和极小值， G是nx4矩阵，
% 其第k行分别是a,p,q,b的第k次迭代值[ak,pk,qk,bk],
% E=[ds,dphi], 分别是s和phis的误差限.

phi=@(x) x^3-2*x-1;
a=-1;b=1;
delta=0.05;epsilon=0.05;

t=(sqrt(5)-1)/2; h=b-a;
phia=feval(phi,a); phib=feval(phi,b);
p=a+(1-t)*h; q=a+t*h;
phip=feval(phi,p);phiq=feval(phi,q);
k=1; G(k,:)=[a, p, q, b];
while(abs(phib-phia)>epsilon) | (h>delta)
    if(phip<phiq)
        b=q; phib=phiq; q=p; phiq=phip;
        h=b-a; p=a+(1-t)*h; phip=feval(phi,p);
    else
        a=p; phia=phip;p=q; phip=phiq;
        h=b-a; q=a+t*h; phiq=feval(phi,q);
    end
    k=k+1; G(k,:)=[a, p, q, b];
end
ds=abs(b-a);dphi=abs(phib-phia);
if(phip<=phiq)
    s=p; phis=phip;
else
    s=q; phis=phiq;
end
E=[ds,dphi];

2.1.2 抛物线法

2.2 非精确线搜索及其Matlab实现

2.2.1 Wolfe准则

Wolfe 准则是指给定 $\rho \in (0,0.5),\sigma \in (\rho,0.5)$ ，求 $\alpha_k$ 使得下面两个不等式同时成立：

其中 $g_k=g(x_k)=\triangledown f(x_k)$

2.2.2 Armijo 准则

Armijo 准则是指给定 $\beta \in (0,1),\sigma \in (0,0.5)$ ，令步长因子 $\alpha _k=\beta^{m_k}$ ，其中 $m_k$ 为满足下列不等式的最小非负整数：

可以证明，若 f(x) 是连续可微的且满足 $g_k^Td_k<0$ ，则 Armijo 准则是有限终止的，即存在正数 $\sigma$ ，使得对于充分大的正整数 m，上式成立.

Armijo 准则

步 0 给定 $\beta \in (0,1),\sigma \in (0,0.5)$ ，令 $m:=0$ .

步 1 若不等式

成立，置 $m_k:=m,x_{k+1}:=x_k+\beta^{m_k}d_k$ ，停算；否则，转步 2

步 2 令 $m:=m+1$ ，转步 1.

2.3 线搜索法的收敛性

线搜索法算法框架

步 0 初始化。选取有关参数及初始迭代点 $x_0\in \mathbb{R} ^n$ ，设定容许误差 $\varepsilon \ll 1$ ，令 k := 0.

步 1 检险终止判别准则.计算 $g_k=\triangledown f(x_k)$ 。若 $||g_k||\leq \varepsilon$ ，输出 $x^*\approx x_k$ ，停算.

步 2 确定下降方向 $d_k$ ，使得满足 $g_k^Td_k<0$ .

步 3 确定步长因子 $\alpha_k$ ，可在下列“精确”与“非精确”两种线搜索技术中选用其一：

(1) 用 0.618 法或二次插值法等精确线搜索技术求

(2) 用前面介绍的 Wolfe 准则或 Armijo 准则等非精确线搜索技术求 $\alpha _k$

步 4 更新迭代点. 令 $x_{k+1}:=x_k+\alpha _kd_k,k:=k+1$ ，转步 1.

第 3 章最速下降法和牛顿法

3.1 最速下降方法及其Matlab实现

最速下降法是用负梯度方向

作为搜索方向的(因此，也称为梯度法)

最速下降法

步 0 选取初始点 $x_0\in \mathbb{R} ^n$ ，容许误差 $0\le \varepsilon \ll 1$ 。令 $k:=1$

步 1 计算 $g_k=\triangledown f(x_k)$ 。若 $||g_k|| \le \varepsilon$ ，停算，输出 $x_k$ 作为近似最优解.

步 2 取方向 $d_k=-g_k$

步 3 由线搜索技术确定步长因子 $\alpha _k$

步 4 令 $x_{k+1}:=x_k+\alpha _kd_k,k:=k+1$ ，转步 1.

设目标函数 f(x) 连续可微且其梯度函数是 Lipschitz 连续的， $\{x_k\}$ 由最速下降法产生，其中步长因子 $\alpha _k$ 由精确线搜索，或由 Wolfe 准则，或由 Armijo 准则产生，则有

最速下降法程序

clear,clc
%function [x,val,k]=grad(fun,gfun,x0)
%功能：用最速下降法求解无约束问题： min f(x)
%输入：x0是初始点，fun, gfun分别是目标函数和梯度
%输出：x, val分别是近似最优点和最优值， k是迭代次数.
maxk=5000; %最大迭代次数
rho=0.5; sigma=0.4;
k=0; epsilon=1e-5;

fun=@(x) 100*(x(1)^2-x(2))^2+(x(1)-1)^2;
gfun=@(x) [400*x(1)*(x(1)^2-x(2))+2*(x(1)-1), -200*(x(1)^2-x(2))]';
x0=[1.1,1.1];

while(k<maxk)
    g=feval(gfun,x0); %计算梯度
    d=-g; %计算搜索方向
    if(norm(d)<epsilon), break; end
    m=0; mk=0;
    while(m<20) %Armijo 搜索
        if(feval(fun,x0+rho*m*d)<feval(fun,x0)+sigma*rho^m*g'*d)
            mk=m; break;
        end
        m=m+1;
    end
    x0(1)=x0(1)+rho^mk*d(1);
    x0(2)=x0(2)+rho^mk*d(2);
    k=k+1;
end
x=x0;
val=feval(fun,x0);

3.2 牛顿法及其Matlab实现

截取其在 $x_k$ 处的泰勒展开式的前三项得

求二次函数 $q_k(x)$ 的稳定点得

求解得牛顿法的迭代公式

其中 $f_k=f(x_k),g_k=\triangledown f(x_k),G_k=\triangledown ^2f(x_k)$ ，要求 $G_k$ 非奇异

基本牛顿法

步 0 给定终止误差值 $0\leq \varepsilon \ll 1$ ，初始点 $x_0 \in \mathbb{R}^n$ 。令 k := 0.

步 1 计算 $g_k=\triangledown f(x_k)$ ，若 $\left \| g_k \right \| \leq \varepsilon$ ，停算，输出 $x^*\approx x_k$ .

步 2 计算 $G_k=\triangledown ^2f(x_k)$ ，并求解线性方程组得解 $d_k$ ， $G_kd=-g_k$

步 3 令 $x_{k+1}=x_k+d_k,k:=k+1$ ，转步 1

牛顿法最突出的优点是收敛速度快，具有局部二阶收敛性

牛顿法的基本思想是用迭代点 $x_k$ 处的一阶导数（梯度）和二阶导数（Hesse 矩阵）对目标函数进行二次函数近似，然后把二次模型的极小点作为新的迭代点，并不断重复这一过程，直至求得满足精度的近似极小点

阻尼牛顿法

步 0 给定终止误差值 $0\le \varepsilon \ll 1,\delta \in (0,1),\sigma \in (0,0.5)$ ，初始点 $x_0\in \mathbb{R}^n$ ，令 k:= 0.

步 1 计算 $g_k=\triangledown f(x_k)$ ，若 $\left \| g_k \right \| \leqslant \varepsilon$ ，停算，输出 $x^*\approx x_k$ .

步 2 计算 $G_k=\triangledown ^2f(x_k)$ ，并求解线性方程组得解 $d_k$ ， $G_kd=-g_k$

步 3 记 $m_k$ 是满足下列不等式的最小非负整数 m.

步 4 令 $\alpha _k =\delta ^{m_k},x_{k+1}=x_k+\alpha _kd_k,k:=k+1$ ，转步 1.

阻尼牛顿法程序

function [x,val,k]=dampnm(fun,gfun,Hess,x0)
%功能：用阻尼牛顿法求解无约束问题： min f(x)
%输入：x0是初始点，fun, gfnn, Hess 分别是求
%    目标函数值,梯度,Hesse矩阵的函数
%输出： x, val分别是近似最优点和最优值, k是迭代次数.
maxk=100; %给出最大迭代次数
rho=0.55; sigma=0.4;
k=0; epsilon=le-5;
while (k<maxk)
    gk=feval(gfun,x0) ; %计算梯度
    Gk=feval(Hess, x0) ; %计算Hesse矩阵
    dk=-Gk\gk; %解方程组Gk*dk=-gk, 计算搜索方向
    if (norm(gk)<epsilon), break; end %检验终止准则
    m=0 ; mk=0;
    while (m<20) % 用Armijo搜索求步长
        if (feval(fun, x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk)
            mk=m; break;
        end
    m=m+l;
end
x0=x0+rh0^mk*dk;
k=k+l;
end
x=x0;
val=feval(fun,x);

3.3 修正牛顿法及其Matlab实现

第 4 章共轭梯度法

共轭梯度法是介于最速下降法与牛顿法之间的一种无约束优化算法，它具有超线性收敛速度，而且算法结构简单，容易编程实现

此外，与最速下降法类似，共轭梯度法只用到了目标函数及其梯度值，避免了二阶导数（Hesse 矩阵）的计算，从而降低了计算量和存储量

4.1 共轭方向法

共轭方向法的基本思想是在求解 n 维正定二次目标函数极小点时产生一组共轭方向作为搜索方向，在精确线搜索条件下算法至多迭代 n 步即能求得极小点

设 G 是 n 阶对称正定矩阵，若 n 维向量组 $d_1,d_2,\cdots,d_m(m\leqslant n)$ 满足

则称 $d_1,d_2,\cdots,d_m$ 为 G 共轭的.

共轭方向法

步 0 给定迭代精度 $0\leq \varepsilon \ll 1$ 和初始点 $x_0$ ，计算 $g_0=\triangledown f(x_0)$ ，选取初始方向 $d_0$ ，使得 $d_0^Tg_0<0$ ，令 k := 0.

步 1 若 $\left \| g_k \right \| \leqslant \varepsilon$ ，停算，输出 $x^*\approx x_k$

步 2 利用精确线搜索方法确定搜索步长 $\alpha _k$ .

步 3 令 $x_{k+1}:=x_k+\alpha _kd_k$ ，并计算 $g_{k+1}=\triangledown f(x_{k+1})$

步 4 选取 $d_{k+1}$ 满足如下下降性和共轭性条件：

步 5 令 $k:=k+1$ ，转步 1.

4.2 共轭梯度法

共轭梯度法是在每一迭代步利用当前点处的最速下降方向来生成关于凸二次函数 f 的 Hesse 矩阵 G 的共轭方向，并建立求 f 在 $\mathbb{R}$ 上的极小点的方法

4.3 共轭梯度法的Matlab程序

function [x,val,k]=frcg(fun,gfun,x0)
% 功能：用FR共机梯度法求解无约束问题： min f(x)
%输入： xO是初始点，fun, gfun分别是目标函数和梯度
%输出： x, val分别是近似最优点和最优值， k是迭代次数.
maxk=5000; %最大迭代次数
rho=0.6;sigma=0.4;
k=0; epsilon=1e-4;
n=length(x0) ;
while (k<maxk)
    g=feval(gfun,x0) ; %计算梯度
    itern=k-(n+1)*floor(k/(n+1));
    itern=itern+1;
    %计算搜索方向
    if (itern==1)
        d=-g;
    else
        beta=(g'*g)/(g0'*g0);
        d=-g+beta*d0; gd=g'*d;
        if(gd>=0.0)
            d=-g;
        end
    end
    if(norm(g)<epsilon), break; end %检验终止条件
    m=0; mk=0;
    while(m<20) %Annij。搜索
        if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)
            mk=m; break;
        end
        m=m+1;
    end
    x0=x0+rho^mk*d;
    val=feval(fun,x0);
    g0=g; d0=d;
    k=k+1;
end
x=x0;
val=feval(fun,x);

第 5 章拟牛顿法

5.1 拟牛顿法及其性质

拟牛顿法的基本思想是在基本牛顿法的步 2 中用 Hesse 矩阵 $G_k=\triangledown ^2f(x_k)$ 的某个近似矩阵 $B_k$ 取代 $G_k$ ，通常， $B_k$ 应具有下面三个特点：

(1) 在某种意义下有 $B_k\approx G_k$ ，使得相应的算法产生的方向近似于牛顿方向，以确保算法具有较快的收敛速度；

(2) 对所有的 k， $B_k$ 是对称正定的，从而使得算法所产生的方向是函数 f 在 $x_k$ 处下降方向；

(3) 矩阵 $B_k$ 更新规则相对比较简单，即通常采用一个秩 1 或秩 2 矩阵进行校正.

f 在 $x_{k+1}$ 处的二次近似模型为

求导得

令 $x=x_k$ ，位移 $s_k=x_{k+1}-x_k$ ，梯度差 $y_k=g_{k+1}-g_k$ ，则有

在拟牛顿法中构造出 Hesse 矩阵的近似矩阵 $B_k$ 满足这种关系式，即

上式通常称为拟牛顿方程或拟牛顿条件，令 $H_{k+1}=B^{-1}_{k+1}$ ，则得到拟牛顿方程的另一个形式：

其中 $H_{k+1}$ 为 Hesse 矩阵逆的近似，搜索方向由 $d_k=-H_kg_k$ 或 $B_kd_k=-g_k$ 确定，根据 $B_k$ 或 $H_k$ 的第三个特点，可令

其中 $E_k$ ， $D_k$ 为秩 1 或秩 2 矩阵。

通常将由上述拟牛顿方程和校正规则所确立的方法称为拟牛顿法

对称 1 校正公式

利用拟牛顿方程对 $H_k$ 进行对称秩 1 修正可得

对称秩 1 算法

步 0 给定初始点 $x_0\in \mathbb{R}^n$ ，终止误差 $0\leq \varepsilon \ll 1$ ，初始对称正定矩阵 $H_0$ (通常取单位矩阵 $I_n$ )，令 k:=0.

步 1 若 $\left \| g_k \right \| \leqslant \varepsilon$ ，停算，输出 $x_k$ 作为近似极小点

步 2 计算搜索方向 $d_k=-H_kg_k$

步 3 用线搜索技术求步长 $\alpha _k$ .

步 4 令 $x_{k+1}=x_k+\alpha _kd_k$ ，由对称秩 1 校正公式确定 $H_{k+1}$ .

步 5 令 k:= k +1，转步 1.

5.2 BFGS算法及其Matlab实现

BFGS 秩 2 修正公式：

若 $B_k$ 对称，则校正后的 $B_{k+1}$ 也对称

设 $B_k$ 对称正定， $B_{k+1}$ 由 BFGS 校正公式确定，那么 $B_{k+1}$ 对称正定的充要条件是 $y^T_ks_k>0$ .

BFGS 算法

步 0 给定参数 $\delta \in(0,1),\sigma \in (0,0.5)$ ，初始点 $x_0\in\mathbb{R}^n$ ，终止误差 $0 \leqslant \varepsilon \ll 1$ ，初始对称正定矩阵 $B_0$ (通常取为 $G(x_0)$ 或单位矩阵 $I_n$ )，令 k:=0.

步 1 计算 $g_k=\triangledown f(x_k)$ ，若 $\left \| g_k \right \| \leqslant \varepsilon$ ，停算，输出 $x_k$ 作为近似极小点.

步 2 解线性方程组得解 $d_k$

步 3 设 $m_k$ 是满足下列不等式的最小非负整数 m：

令 $\alpha _k=\delta ^{m_k},x_{k+1}=x_k+\alpha_kd_k$

步 4 由校正公式确定 $B_{k+1}$ .

步 5 令 k:=k+1，转步 1.

基于 Armijo 搜索的 BFGS 算法的 Matlab 程序

function [x,val,k]=bfgs(fun,gfun,x0,varargin)
%功能：用BFGS算法求解无约束问题： min f(x)
%输入：x0是初始点，fun, gfun分别是目标函数及其梯度；
% varargin是输入的可变参数变量，简单调用bfgs时可以忽略它，
% 但若其他程序循环调用该程序时将发挥重要的作用
%输出：x, val分别是近似最优点和最优值，k是迭代次数.
maxk=500; %给出最大迭代次数
rho=0.55; sigma=0.4; epsilon=1e-5;
k=0; n=length(x0);
Bk=eye(n); %Bk=feval('Hess',x0);
while(k<maxk)
    gk=feval(gfun,x0,varargin{:});%计算梯度
    if(norm(gk)<epsilon), break; end %检验终止准则
    dk=-Bk\gk; %解方程组，计算搜索方向
    m=0; mk=0;
    while(m<20) % 用Armijo搜索求步长
        newf=feval(fun,x0+rho^m*dk,varargin{:});
        oldf=feval(fun,x0,varargin{:});
        if(newt<oldf+sigma*rho^m*gk'*dk)
            mk=m; break;
        end
        m=m+l;
    end
    %BFGS校正
    x=x0+rho^mk*dk;
    sk=x-xO; yk=feval(gfun,x,varargin{:})-gk;
    if(yk'*sk>0)
        Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);
    end
    k=k+l; x0=x;
end
val=feval(fun,x0,varargin{:});

5.3 DFP算法及其Matlab实现

DFP 校正公式

若 $H_k$ 对称，则校正后的 $H_{k+1}$ 也对称

设 $H_k$ 对称正定， $H_{k+1}$ 由 DFP 校正公式确定，那么 $H_{k+1}$ 对称正定的充要条件是 $s^T_ky_k>0$

当采用精确线搜索或 Wolfe 搜索准则时，矩阵序列 $\{H_k\}$ 的正定性条件 $s^T_ky_k>0$ 可以被满足。但一般来说 Armijo 搜索准则不能满足这一条件，需要作如下修正：

基于 Armijo 搜索准则的 DFP 算法：

步 0 给定参数 $\delta \in(0,1),\sigma \in (0,0.5)$ ，初始点 $x_0\in \mathbb{R}^n$ ，终止误差 $0 \leqslant \varepsilon \ll 1$ ，初始对称正定矩阵 $H_0$ (通常取为 $G(x_0)^{-1}$ 或单位矩阵 $I_n$ )，令 k:=0

步 1 计算 $g_k=\triangledown f(x_k)$ ，若 $\left \| g_k \right \| \leqslant \varepsilon$ ，停算，输出 $x_k$ 作为近似极小点.

步 2 计算搜索方向 $d_k=-H_kg_k$

步 3 设 $m_k$ 是满足下列不等式的最小非负整数 m：

令 $\alpha_k=\delta ^{m_k},x_{k+1}=x_k+\alpha_kd_k$

步 4 由校正公式确定 $H_{k+1}$ .

步 5 令 k:= k +1，转步 1.

DFP 算法程序

function [x,val,k]=dfp(fun,gfun,xO)
%功能：用DFP算法求解无约束问题：min f(x)
%输入：x0是初始点，fun, gfun分别是目标函数及其梯度
%输出：x, val分别是近似最优点和袁优值，k是迭代次数.
maxk=le5; %给出最.大选代次数
rho=0.55;sigma=0.4; epsilon=le-5;
k=0; n=length.(x0);
Hk=inv (f eval( *Hess 3
,x0)) ; %Hk=eye (n) ;
while(k＜maxk)
    gk=feval(gfun,xO); %计算梯度
    if (norm(gk) 〈epsilon), break; end %检验终止准则
    dk=-Hk*gk; 7解方程组，计算搜索方向
    m=0; mk=O;
    while(m<20) % 用Armijo搜索求步长
        if(feval(fun,xO+rhcTm*dk)<feval(fun,xO)+sigma*rhoCm*gk'*dk)
            mk=m; break;
        end
        m=m+l;
    end
    %DFP校正
    x=x0+rho^mk*dk;
    sk=x-x0; yk=feval(gfun,x)-gk;
    if(sk>*yk>0)
        Hk=Hk-(Hk*yk*yk'*Hk)/(yk'*Hk*yk)+(sk*sk')/(sk'*yk);
    end
    k=k+l; x0=x;
end
val=feval(fun,x0);

5.4 Broyden族算法及其Matlab实现

关于 $H_k$ 的 Broyden 族校正公式为

其中 $\phi _k$ 为实参数， $v_k$ 由下式定义:

5.5 拟牛顿法的收敛性

Armijo 准则，令步长因子 $\alpha_k=\beta^{m_k}$ ，其中 $m_k$ 为满足下列不等式的最小非负整数：

BFGS 算法的迭代公式

假设

(1) 函数 f(x) 在 $\mathbb{R}^n$ 上二阶连续可微；

(2) 水平集

是凸集，并且函数 f 在 $\mathcal{L}(x_0)$ 上一致凸，即存在常数 $0<m\leqslant M$ ，使得

(3) 存在 $x^*$ 的一个邻域 $N(x^*,\delta )$ ，使得 $G(x)=\triangledown ^2f(x)$ 在该邻域内 Lipschitz 连续，即存在常数 L > 0，使得

定理：设 $\{B_k\}$ 是由 BFGS 校正公式产生的非奇异矩阵序列， $\alpha_k$ 为满足 Armijo 准则的步长。若 f(x) 满足假设 (1) 和 (2)，那么由 BFGS 迭代公式产生的序列 $\{x_k\}$ 全局收敛到 f(x) 的极小点 $x^*$

第 6 章信赖域方法

信赖域方法与线搜索技术一样，也是优化算法中的一种保证全局收敛的重要技术，它们的功能都是在优化算法中求出每次迭代的位移，从而确定新的迭代点。所不同的是：

线搜索技术是先产生位移方向（也称为搜索方向），然后确定位移的长度（也称为搜索步长）；

而信赖域技术则是直接确定位移，产生新的迭代点.

信赖域方法的基本思想是：首先给定一个所谓的“信赖域半径”作为位移长度的上界，并以当前迭代点为中心，此“上界”为半径“画地为牢”，确定一个被称为“信赖域”的闭球区域。然后，通过求解这个区域内的"信赖域子问题”（目标函数的二次近似模型）的最优点来确定“候选位移”。

若候选位移能使目标函数值有充分的下降量，则接受该候选位移作为新的位移，并保持或扩大信赖域半径，继续新的迭代；

否则，说明二次模型与目标函数的近似度不够理想，需要缩小信赖域半径，再通过求解新的信赖域内的子问题得到新的候选位移.

如此重复下去，直到满足迭代终止条件.

6.1 信赖域方法的基本结构

设 $x_k$ 是第 k 次迭代点，记 $f_k=f(x_k),g_k=\triangledown f(x_k)$ ， $B_k$ 是 Hesse 矩阵 $\triangledown ^2f(x_k)$ 的第 k 次近似，则第 k 次迭代步的信赖域子问题具有如下形式：

其中 $\Delta _k$ 为信赖域半径，|| • || 为任一种向量范数，通常取 2 范数或 $\infty$ 范数.

设上述子问题的最优解为 $d_k$ ，定义 $\Delta f_k$ 为 f 在第 k 步的实际下降量

$\Delta q_k$ 为对应的预测下降量

再定义它们的比值为

一般地有 $\Delta q_k>0$ ，因此，若 $r_k<0$ ，则 $\Delta f_k <0,x_k+d_k$ 不能作为下一个迭代点，需要缩小信赖域半径重新求解子问题。若 $r_k$ 比较接近 1，则说明二次模型与目标函数在信赖域范围内有很好的近似，此时 $x_{k+1}:=x_k+d_k$ 可以作为新的迭代点，同时下一次迭代时可以增大信赖域半径。对于其他情况，信赖域半径可以保持不变。

信赖域方法

步 0 选取初始参数 $0\leqslant \eta _1 < \eta _2 <1,0<\tau_1<1<\tau_2,0\leqslant\varepsilon \ll 1,x_0\in \mathbb{R}^n$ ，取定 $\tilde{\Delta } >0$ 为信赖域半径的上限，初始信赖域半径 $\Delta _0\in (0,\tilde{\Delta}]$ ，令 $k:=0$

步 1 计算 $g_k=\triangledown f(x_k)$ ，若 $\left \| g_k \right \| \leqslant \varepsilon$ 停止迭代.

步 2 求解子问题的解 $d_k$ .

步 3 按 $r_k=\frac{\Delta f_k}{\Delta q_k}$ 计算 $r_k$ 的值.

步 4 校正信赖域半径

步 5 若 $r_k>\eta_1$ ，则令 $x_{k+1}:=x_k+d_k$ ，更新矩阵 $B_k$ 到 $B_{k+1}$ ，令 $k:=k+1$ ，转步 1；否则， $x_{k+1}:=x_k$ 外，令 $k:=k+1$ ，转步 2.

在上述算法中一组推荐的参数值为

在实际计算中，可以上述参数进行调整，以达到最佳计算效果

6.2 信赖域方法的收敛性

6.3 信赖域子问题的求解

求解子问题的光滑牛顿法的 Matlab 程序

function [d,val,lam,k]==trustq(gk,Bk,dta)
%功能：求解信赖域子问题： min qk(d)=gk'*d+0.5*d'*Bk*d, s.t. ||d||<=dalta
%输入： gk是xk处的梯度，Bk是第k次近似Hesse矩阵，dta是当前信赖域半径
%输出： d, val分别是子问题的最优点和最优值，lam是乘子值，k是迭代次数.
n=length(gk); gamma=0.05;
epsilon=1.0e-6; rho=0.6; sigma=0.2;
mu0=0.05; lam0=0.05;
d0=ones(n,1); u0=[mu0,zeros(1,n+1)]';
z0=[mu0, lam0, d0']';
k=0; %k为迭代次数
z=z0; nu=mu0; lam=lam0; d=d0;
while (k<=150)
    dh=dah(mu,lam,d,gk,Bk,dta);
    if (norm(dh)<epsilon)
        break;
    end
    A=JacobiH(mu,lam,d,Bk,dta);
    b=beta(mu,lam,d,gk,Bk,dta,gamma)*u0-dh;
    B=inv(A); dz=B*b;
    dmu=dz(1); dlam=dz(2); dd=dz(3:n+2);
    m=0; mk=0;
    while (m<20)
        dhnew=dah(mu+rho^m*dmu,lam+rho^m*dlam,d+rho^m*dd,gk,Bk,dta);
        if (norm(dhnew)<=(1-sigma*(l-gamma*mu0)*rho^m)*dh)
            mk=m;
            break;
        end
        m=m+1;
    end
    alpha=rho^mk;
    mu=mu+alpha*dmu;
    lam=lam+alpha*dlam;
    d=d+alpha*dd;
    k=k+l;
end
val=gk'*d+0.5*d'*Bk*d;

function p=phi(mu,a,b)
p=a+b-sqrt((a-b)^2+4*mu);

function dh=dah(mu,lam,d,gk,Bk,dta)
n=length(d);
dh(l)=mu; dh(2)=phi(mu,lam,dta^2-norm(d)^2);
mh=(Bk+lam*eye(n))*d+gk;
for(i=l:n)
    dh(2+i)=mh(i);
end
dh=dh(:);

function bet=beta(mu,lam,d,gk,Bk,dta,gamma)
dh=dah(mu,lam,d,gk,Bk,dta);
bet=gamma*norm(dh)*min(1,norm(dh));

function A=JacobiH(mu,lam,d,Bk,dta)
n=length(d);
A=zeros(n+2,n+2);
pmu=-4*mu/sqrt((lam+norm(d)*2-dta*2)*2+4*mu^2);
thetak=(lam+norm(d)*2-dta*2)/sqrt((lam+norm(d)^2-dta^2)^2+4*mu^2);
A=[l,          0,         zeros(1,n);
   pmu,        1-thetak,  -2*(1+thetak)*d';
   zeros(n,1), d,         Bk+lam*eye(n)];

6.4 信赖域方法的Matlab程序

function [xk,val,k]=trustm(x0)
%功能：牛顿型信赖域方法求解无约束优化问题 min f(x)
%输入：X0是初始迭代点
%输出：xk是近似极小点，val是近似极小值，k是迭代次数
n=length(x0); x=x0; dta=l;
etal=0.1; eta2=0.75; dtabar=2.0;
taul=0.5; tau2=2.0; epsilon=1e-6;
k=0; Bk=Hess(x) ;
while (k<50)
    gk=gfun(x) ;
    if(norm(gk)<epsilon)
        break;
    end
    % 调用子程序trustq
    [d,val,lam,ik]=trustq(gk,Bk,dta);
    deltaq=-qk(x,d);
    deltaf=fun(x)-fun(x+d);
    rk=deltaf / deltaq;
    if (rk<=etal)
        dta=tau1*dta;
    else if(rk>=eta2 & norm(d)==dta)
            dta=min(tau2*dta,dtabar);
        else
            dta=dta;
        end
    end
    if (rk>etal)
    x=x+d;
    Bk=Hess(x);
    end
    k=k+l;
end
xk=x;
val=fun(xk) ;

第 7 章非线性最小二乘问题

约束优化问题可以通过 KKT 条件与非线性方程组建立起重要的关系

7.1 Gauss-Newton法

记 $F(x)=(F_1(x),F_2(x),\cdots,F_m(x))^T$ ，则非线性最小乘问题可以表示为

目标函数 f 的梯度和 Hesse 矩阵分别为

其中

利用牛顿型迭代算法

便得到求解非线性最小二乘问题的迭代算法

在标准假设下，容易得到该算法的收敛性质。缺点是 $S(x)$ 中 $\triangledown ^2F_i(x)$ 的计算量较大，如果忽略这一项，便得到求解非线性最小二乘问题的 Gauss-Newton 迭代算法

其中

称为 Gauss-Newton 方向

7.2 Levenberg-Marquardt方法

7.3 L-M算法的Matlab程序

第 8 章最优性条件

8.1 等式约束问题的最优性条件

作该问题的拉格朗日函数

下面的拉格朗日定理描述了该问题取极小值的一阶必要条件，也就是所谓的 KT 条件

假设 x* 是该问题的局部极小点， $f(x)$ 和 $h_i(x)(i=1,2,\cdots,l)$ 在 x* 的某邻域内连续可微，若向量组 $\triangledown h_i(x^*)(i=1,2,\cdots,l)$ 线性无关，则存在乘子向量 $\lambda^*=(\lambda^*_1,\lambda^*_2,\cdots,\lambda^*_l)^T$ ，使得

即

8.2 不等式约束问题的最优性条件

KT 条件

设 x* 是上述不等式约束问题的局部极小点，有效约束集 $I(x^*)=\{i|g_i(x^*)=0\}$ ，并设 f(x) 和 $g_i(x)(i=1,\cdots,m)$ ，在 x* 处可微，若向量 $\triangledown g_i(x^*)(i\in I(x^*))$ 线性无关，则存在向量 $\lambda^*=(\lambda^*_1,\cdots,\lambda^*_m)$ ，使得

8.3 一般约束问题的最优性条件

8.4 鞍点和对偶问题

第 9 章罚函数法

罚函数法的基本思想是：根据约束条件的特点，将其转化为某种惩罚函数加到目标函数中去，从而将约束优化问题转化为一系列的无约束优化问题来求解.

9.1 外罚函数法

由等式约束得 $x_2=1-x_1$ ，代入目标函数得到一个无约束的单变量极小化问题

其全局极小点为 $x^*_1=0.5$ ，从而得到原问题的全局极小点为 $x^*=(0.5,0.5)^T$

现在要使构造的罚函数 $\bar{P}(x)$ 满足

只要令 $\bar{P}(x)=(x_1+x_2-1)^2$ 即可

现在考察目标函数和上述罚函数的组合

其中 $\sigma >0$ 为充分大的正数，称为罚参数或罚因子.

求这个组合函数的极小点，由

得

求解上述方程组得

令 $\sigma \rightarrow +\infty$ 有

这样就从无约束优化问题极小点的极限得到了原问题的极小点

下面将这种思想方法推广到一般约束的优化问题，考虑

记可行域为 $\mathcal{D} =\{x\in \mathbb{R}^n|h_i(x)=0(i\in E),g_i\geqslant 0(i\in I)\}$ ，构造罚函数

和增广目标函数

其中 $\sigma >0$ 为罚参数或罚因子.

当 $x\in \mathcal{D}$ ，即 x 为可行点时， $P(x,\sigma )=f(x)$ ，此时，目标函数没有受到额外惩罚；

而当 $x\notin \mathcal{D}$ ，即 x 为不可行点时， $P(x,\sigma )>f(x)$ ，此时，目标函数受到了额外的惩罚.

$\sigma >0$ 越大，受到的惩罚越重，当 $\sigma >0$ 充分大时，要使 $P(x,\sigma )$ 达到极小，罚函数 $\bar{P}(x)$ 应充分小才可以，从而 $P(x,\sigma )$ 的极小点充分逼近可行域 $\mathcal{D}$ ，而其极小值自然充分逼近 f(x) 在 $\mathcal{D}$ 上的极小值。这样求解一般约束优化问题就可以化为求解一系列无约束的优化问题

其中 $\{\sigma _k\}$ 为正数序列且 $\sigma _k\rightarrow +\infty$ .

外罚函数法

步 0 给定初始点 $x_0\in \mathbb{R}^n$ ，终止误差 $0\leqslant \varepsilon \ll 1,\sigma _1>0,\gamma >1$ ，令 k := 1.

步 1 以 $x_{k-1}$ 为初始点求解子问题

令其极小点为 $x_k$

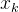
步 2 若 $\sigma _k\bar{P}(x_k)\leqslant \varepsilon$ ，停算，输出 $x^*\approx x_k$ 作为如似极小点.

步 3 令 $\sigma_{k+1}:=\gamma \sigma _k,k:=k+1$ ，转步 1

9.2 内点法

9.3 乘子法

9.4 乘子法的Matlab实现

第 10 章可行方向法

10.1 Zoutendijk可行方向法

10.2 梯度投影法

10.3 简约梯度法

第 11 章二次规划

二次规划是非线性优化中的一种特殊情形，它的目标函数是二次实函数，约束函数都是线性函数。

11.1 等式约束凸二次规划的解法

11.1.1 零空间方法

11.1.2 拉格朗日方法及其 Matlab 程序

11.2 一般凸二次规划的有效集方法

第 12 章序列二次规划法

的序列二次规划 (SQP) 方法。SQP 方法的基本思想是：在每一迭代步通过求解一个二次规划子问题来确立一个下降方向，以减少价值函数来取得步长，重复这些步骤直到求得原问题的解。

12.1 牛顿-拉格朗日法

该问题的拉格朗日函数为

其中 $\mu=(\mu_1,\cdots,\mu_l)^T$ 为拉格朗日乘子向量

约束函数 $h(x)$ 的梯度矩阵为

则 h(x) 的 Jacobi 矩阵为 $A(x)=\triangledown h(x)^T$ .

根据上述问题的 KT 条件，可以得到

考虑用牛顿法求解上述非线性方程组，记函数 $\triangledown L(x,\mu)$ 的 Jacobi 矩阵为

其中

是拉格朗日函数 $L(x,\mu)$ 关于 x 的 Hesse 矩阵

矩阵 $N(x,\mu)$ 也称为 KT 矩阵.

对于给定的点 $z_k=(x_k,\mu_k)$ ，牛顿法的迭代格式为

其中 $p_k=(d_k,v_k)$ 满足

即

牛顿-拉格朗日方法

步 0 选取 $x_0\in \mathbb{R}^n,\mu_0\in \mathbb{R}^l,\rho,\gamma \in (0,1),0\leqslant \varepsilon \ll 1$ ，令 k := 0

步 1 计算 $\left \| \triangledown L(x_k,\mu_k) \right \|$ 的值，若 $\left \| \triangledown L(x_k,\mu_k) \right \| \leqslant \varepsilon$ 停算。否则，转步 2

步 2 解上述方程组得 $p_k=(d_k,v_k)$ .

步 3 若

则置 $\alpha_k:=1$ ，转步 5；否则，转步 4.

步 4 令 $m_k$ 是使下面的不等式成立的最小非负整数 m：

置 $\alpha_k=\rho^{m_k}$ .

步 5 令 $x_{k+1}=x_k+\alpha _kd_k,\mu_{k+1}=\mu_k+\alpha_kv_k$ ，置 k := k + 1，转步 1.