机器人视觉初级系列(5) - 图像边缘检测

目的：

边缘检测算子很多，基本上都是对图像开一阶导数或者二阶导数，如果将边缘认为是一定数量点亮度发生变化的地方，那么边缘检测大体上就是计算这个亮度变化的导数。这次学习进一步了解图像边缘检测的算子。

任务：

写一个彩色图片中的物体进行边缘检测，能识别出物体的特征区域轮廓；

---

边缘检测

边缘检测的三个主要评价标准是:

• 低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报。
• 高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近。
• 最小响应: 图像中的边缘只能标识一次。

不同图像灰度不同，边界处一般会有明显的边缘，利用此特征可以分割图像。需要说明的是：边缘和物体间的边界并不等同，边缘指的是图像中像素的值有突变的地方，而物体间的边界指的是现实场景中的存在于物体之间的边界。有可能有边缘的地方并非边界，也有可能边界的地方并无边缘，因为现实世界中的物体是三维的，而图像只具有二维信息，从三维到二维的投影成像不可避免的会丢失一部分信息；另外，成像过程中的光照和噪声也是不可避免的重要因素。正是因为这些原因，基于边缘的图像分割仍然是当前图像研究中的世界级难题，目前研究者正在试图在边缘提取中加入高层的语义信息。

在实际的图像分割中，往往只用到一阶和二阶导数，虽然，原理上，可以用更高阶的导数，但是，因为噪声的影响，在纯粹二阶的导数操作中就会出现对噪声的敏感现象，三阶以上的导数信息往往失去了应用价值。二阶导数还可以说明灰度突变的类型。在有些情况下，如灰度变化均匀的图像，只利用一阶导数可能找不到边界，此时二阶导数就能提供很有用的信息。二阶导数对噪声也比较敏感，解决的方法是先对图像进行平滑滤波，消除部分噪声，再进行边缘检测。不过，利用二阶导数信息的算法是基于过零检测的，因此得到的边缘点数比较少，有利于后继的处理和识别工作。

各种算子的存在就是对这种导数分割原理进行的实例化计算，是为了在计算过程中直接使用的一种计算单位。

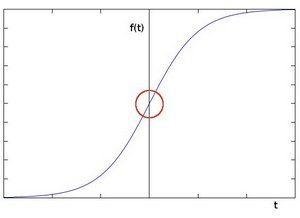
为什么对图像进行求导是重要的呢? 假设我们需要检测图像中的 边缘 ，到在物体边缘处，像素值明显改变。导数可以用来表示这一像素值得改变。梯度值的大变预示着图像中内容的变化。如下图：

用更加形象的图像来解释，假设我们有一张一维图形。下图中灰度值的”跃升”表示边缘的存在：

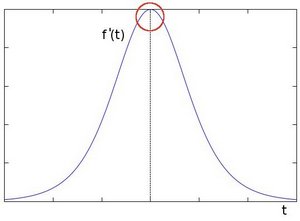
使用一阶微分求导我们可以更加清晰的看到边缘“跃升”的存在(这里显示为高峰值)

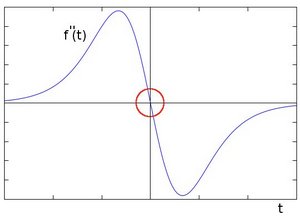
从上面可以推论检测边缘可以通过梯度值大于邻域的像素方法找到。以上就是一阶导数检测图像边缘，如果在边缘部分求二阶导数会出现什么情况？

在一阶导数的极值位置，二阶导数为0。所以我们也可以用这个特点来作为检测图像边缘的方法。 但是， 二阶导数的0值不仅仅出现在边缘(它们也可能出现在无意义的位置)，不过可以过滤掉这些点。

---

1.Sobel算子

Sobel算子其主要用于边缘检测，在技术上它是以离散型的差分算子，用来运算图像亮度函数的梯度的近似值， Sobel算子是典型的基于一阶导数的边缘检测算子，由于该算子中引入了类似局部平均的运算，因此对噪声具有平滑作用，能很好的消除噪声的影响。Sobel算子对于象素的位置的影响做了加权，与Prewitt算子、Roberts算子相比因此效果更好。

Sobel 算子结合了高斯平滑和微分求导，它是一个离散微分算子 (discrete differentiation operator)。用来计算图像灰度函数的近似梯度。

Sobel算子包含两组 $3*3$ 的矩阵，分别为横向及纵向模板，将之与图像作平面卷积，即可分别得出横向及纵向的亮度差分近似值。实际使用中，常用如下两个模板来检测图像边缘。

算法实现

首先在在两个方向求导:

1.水平变化: 将图像 $I$ 与一个奇数大小的内核 $G_x$ 进行卷积。比如，当内核大小为3时，$G_x$ 的计算结果为:

$$G_{x}= \left[ \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{matrix} \right] *I$$

2.垂直变化: 将图像 $I$ 与一个奇数大小的内核$G_{y}$ 进行卷积。比如，当内核大小为3时, $G_{y}$ 的计算结果为:

Gy=⎡⎣⎢⎢−101−202−