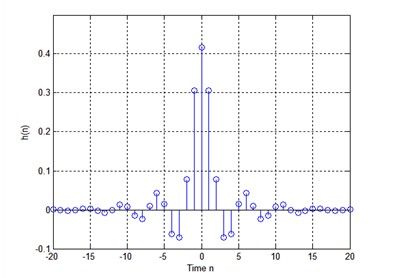
就如同之前所说的一样,使用下图所示的单位冲击响应,所设计的滤波器,是无法实现的。
现在,让我们看看其这个滤波器的频响。所谓频响,就是计算其单位冲击响应的离散时间傅里叶变换,
我们可以看出,这个滤波器的频响的计算结果是实数,并没有虚数部分。也就是,其相位谱一直是0,也就意味着,这个滤波器输入与输出之间没有延迟,这种相位特性称为0延迟相位特性。
但是,这个滤波器无法是无法实现的。我们实际计算一下该滤波器的输入输出,就可以明白。
这个滤波器在计算的过程中,需要过去的值和未来的值。未来的值是不可预测的,所以,这个滤波器无法实现。为了使得这个滤波器可以实现,我们只好移动其单位冲击响应,使得其不再需要未来的值。比如,就像下面这样移动。
这样的话,这个滤波器就可以实现了,我们只需要记录其40个过去的输入值和现在的输入值。但是,由于移动了其单位冲击响应,会不会对频响产生什么影响呢,我们来看看。
为了更好的说明问题,L去代替之前例子中的20。
移动之后频响,我们根据上面式子可以得出两个结论:1,移动不会对幅度谱产生影响。2,,移动会对相位产生一个延迟,这个延迟主要取决于移动的长度,移动的长度越长,延迟越大。但是,这个移动是线性的。
因此,我们把这个移动的相位特性称为,线性相位特性。到这里,我们移动后的,因果的,可实现的滤波器的单位冲击响应,如下所示。
2.窗函数实现的FIR滤波器代码(C语言)
- #include <stdio.h>
- #include <math.h>
- #include <malloc.h>
- #include <string.h>
- #define pi (3.1415926)
- /*-------------Win Type----------------*/
- #define Hamming (1)
- double Input_Data[] =
- {
- 0.000000 , 0.896802 , 1.538842 , 1.760074 , 1.538842 , 1.000000 , 0.363271 , -0.142040 , -0.363271 , -0.278768,
- 0.000000 , 0.278768 , 0.363271 , 0.142020 , -0.363271 , -1.000000 , -1.538842 , -1.760074 , -1.538842 , -0.896802,
- 0.000000 , 0.896802 , 1.538842 , 1.760074 , 1.538842 , 1.000000 , 0.363271 , -0.142040 , -0.363271 , -0.278768,
- 0.000000 , 0.278768 , 0.363271 , 0.142020 , -0.363271 , -1.000000 , -1.538842 , -1.760074 , -1.538842 , -0.896802,
- 0.000000 , 0.896802 , 1.538842 , 1.760074 , 1.538842 , 1.000000 , 0.363271 , -0.142040 , -0.363271 , -0.278768,
- 0.000000 , 0.278768 , 0.363271 , 0.142020 , -0.363271 , -1.000000 , -1.538842 , -1.760074 , -1.538842 , -0.896802,
- 0.000000 , 0.896802 , 1.538842 , 1.760074 , 1.538842 , 1.000000 , 0.363271 , -0.142040 , -0.363271 , -0.278768,
- 0.000000 , 0.278768 , 0.363271 , 0.142020 , -0.363271 , -1.000000 , -1.538842 , -1.760074 , -1.538842 , -0.896802,
- 0.000000 , 55
- };
- double sinc(double n)
- {
- if(0==n) return (double)1;
- else return (double)(sin(pi*n)/(pi*n));
- }
- int Unit_Impulse_Response(int N,double w_c,
- int Win_Type,
- double *Output_Data)
- {
- signed int Count = 0;
- for(Count = -(N-1)/2;Count <= (N-1)/2;Count++)
- {
- *(Output_Data+Count+((N-1)/2)) = (w_c/pi)*sinc((w_c/pi)*(double)(Count));
- //printf("%d %lf ",Count+((N-1)/2)+1,*(Output_Data+Count+((N-1)/2)));
- //if(Count%4 == 0) printf("\n");
- }
- switch (Win_Type)
- {
- case Hamming: printf("Hamming \n");
- for(Count = -(N-1)/2;Count <= (N-1)/2;Count++)
- {
- *(Output_Data+Count+((N-1)/2)) *= (0.54 + 0.46 * cos((2*pi*Count)/(N-1)));
- //printf("%d %lf ",Count+((N-1)/2)+1,*(Output_Data+Count+((N-1)/2)));
- //if(((Count+1)%5 == 0)&&(Count != -20)) printf("\n");
- }
- break;
- default: printf("default Hamming \n");
- for(Count = -(N-1)/2;Count <= (N-1)/2;Count++)
- {
- *(Output_Data+Count+((N-1)/2)) *= (0.54 + 0.46 * cos((2*pi*Count)/(N-1)));
- //printf("%d %lf ",Count+((N-1)/2)+1,*(Output_Data+Count+((N-1)/2)));
- //if(((Count+1)%5 == 0)&&(Count != -20)) printf("\n");
- }
- break;
- }
- return (int)1;
- }
- void Save_Input_Date (double Scand,
- int Depth,
- double *Input_Data)
- {
- int Count;
- for(Count = 0 ; Count < Depth-1 ; Count++)
- {
- *(Input_Data + Count) = *(Input_Data + Count + 1);
- }
- *(Input_Data + Depth-1) = Scand;
- }
- double Real_Time_FIR_Filter(double *b,
- int b_Lenth,
- double *Input_Data)
- {
- int Count;
- double Output_Data = 0;
- Input_Data += b_Lenth - 1;
- for(Count = 0; Count < b_Lenth ;Count++)
- {
- Output_Data += (*(b + Count)) *
- (*(Input_Data - Count));
- }
- return (double)Output_Data;
- }
- int main(void)
- {
- double w_p = pi/10;
- double w_s = pi/5;
- double w_c = (w_s + w_p)/2;
- printf("w_c = %f \n" , w_c);
- int N = 0;
- N = (int) ((6.6*pi)/(w_s - w_p) + 0.5);
- if(0 == N%2) N++;
- printf("N = %d \n" , N);
- double *Impulse_Response;
- Impulse_Response = (double *) malloc(sizeof(double)*N);
- memset(Impulse_Response,
- 0,
- sizeof(double)*N);
- Unit_Impulse_Response(N,w_c,
- Hamming,
- Impulse_Response);
- double *Input_Buffer;
- double Output_Data = 0;
- Input_Buffer = (double *) malloc(sizeof(double)*N);
- memset(Input_Buffer,
- 0,
- sizeof(double)*N);
- int Count = 0;
- FILE *fs;
- fs=fopen("FIR_Data.txt","w");
- while(1)
- {
- if(Input_Data[Count] == 55) break;
- Save_Input_Date (Input_Data[Count],
- N,
- Input_Buffer);
- Output_Data = Real_Time_FIR_Filter(Impulse_Response,
- N,
- Input_Buffer);
- fprintf(fs,"%lf,",Output_Data);
- //if(((Count+1)%5 == 0)&&(Count != 0)) fprintf(fs,"\r\n");
- Count++;
- }
- /*---------------------display--------------------------------
- for(Count = 0; Count < N;Count++)
- {
- printf("%d %lf ",Count,*(Input_Buffer+Count));
- if(((Count+1)%5 == 0)&&(Count != 0)) printf("\n");
- }
- */
- fclose(fs);
- printf("Finish \n");
- return (int)0;
- }
3.频响的问题
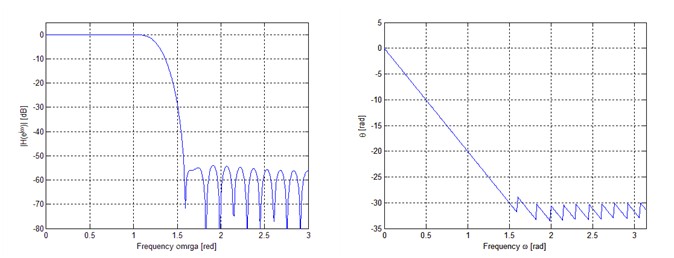
按照上面程序,参数如下设定。
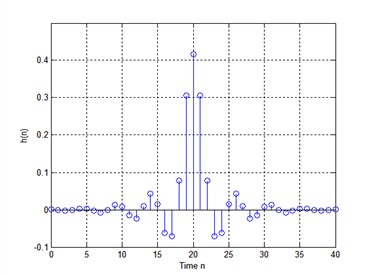
运行程序,我们就实现了一个FIR滤波器。我们使用Matlab做出其频响。
好了,这里可以看出,从其幅度特性看来,我们确实实现了一个低通滤波器。但是,相位特性就比较奇怪(为了方便看出问题,我已经进行了解卷绕,至于什么是解卷绕,为什么要解卷绕,之后会说)。
那么,问题来了!按照道理来说,这个FIR滤波器应该是拥有线性相位特性的,但是为什么这里的线性相位特性确不是一条直线!在接近于阻带起始频率的地方,有什么会震荡?这个问题,之后再解决吧。
[数字信号处理]相位特性解卷绕 <-----------戳我
4.实际的滤波效果
为了验证效果,我们输入实际的信号看看。这里,我们选择采样周期为10ms,那么,其通带频率和阻带起始频率为
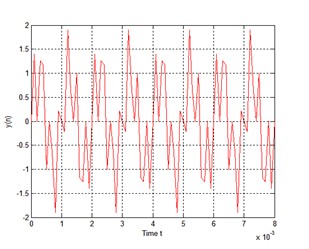
为了验证其性质,我选择了1KHz和3KHz的频率混合,最终输出。输入的波形如下。
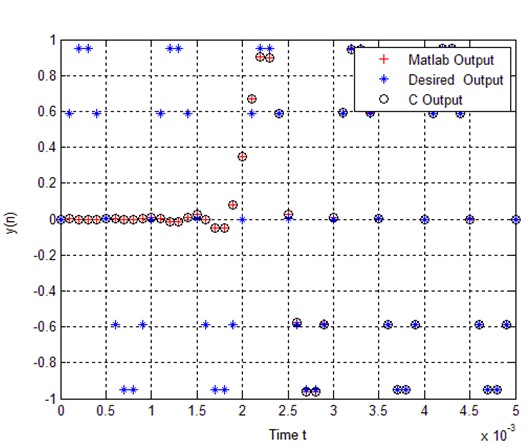
其输出波形是如下。
红色的“+”是Matlab计算的结果,黑的o是我用C语言实现的滤波器的计算结果,蓝的*号是1KHz的信号,也就是希望的输出。可以看出,这个滤波器有一定的延迟,但是滤波效果还是不错。
from: http://blog.csdn.net/thnh169/







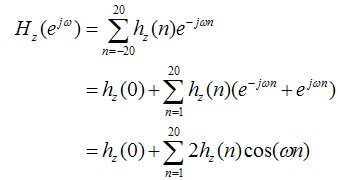
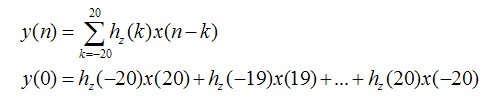
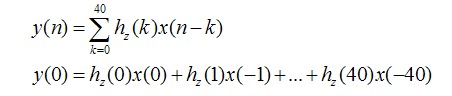
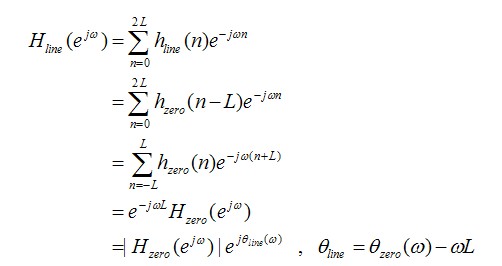

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








