贝叶斯神经网络（Bayesian Neural Network, BNN）

原创于 2025-08-08 18:36:41 发布 · 944 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #深度学习 #人工智能 #开发语言 #python #机器学习 #数据挖掘

机器学习与人工智能专栏收录该内容

57 篇文章

订阅专栏

该文章已生成可运行项目，

贝叶斯神经网络的核心难点在于概率框架与传统神经网络的结合。我需要强调三个关键点：1) 如何用概率分布替代权重点估计 2) 推断方法的选择策略 3) 实际应用时的计算权衡。尤其要解释清楚变分推断和MCMC的取舍——用户如果实际部署模型，肯定会面临这个抉择。

贝叶斯神经网络（Bayesian Neural Network, BNN） 是传统神经网络与贝叶斯概率框架结合的产物。它通过引入不确定性量化，解决了传统神经网络的三大痛点：

过度自信预测（对错误预测仍输出高概率）
小数据过拟合
决策缺乏可解释性

一、核心思想：从点估计到概率分布

传统神经网络	贝叶斯神经网络
权重是固定值（点估计）	权重是概率分布（如高斯分布）
输出单一预测结果	输出预测分布（含不确定性）
无法量化模型自身的不确定性	区分认知不确定性（模型不确定性）与偶然不确定性（数据噪声）

https://miro.medium.com/v2/resize:fit:1400/1*9yMZ5iwdD6s2nY5Y7C3yMg.png

二、关键机制：贝叶斯推断

BNN 的核心是将神经网络中的权重 ww 视为随机变量，通过贝叶斯定理计算后验分布：

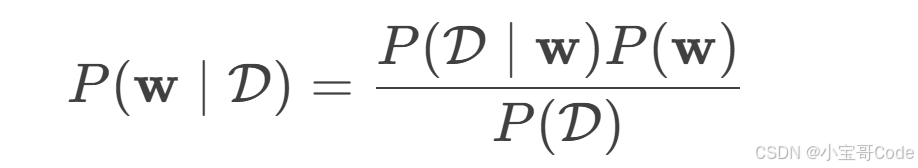
P(w)P(w)：权重的先验分布（如高斯先验）
P(D∣w)P(D∣w)：似然函数（数据在给定权重下的概率）
P(w∣D)P(w∣D)：后验分布（目标）

难点：后验分布计算复杂（分母 P(D)P(D) 难解），需用近似推断方法。

三、训练：近似推断方法

1. 马尔可夫链蒙特卡洛（MCMC）

通过采样（如Hamiltonian Monte Carlo）逼近后验分布
优点：理论精确
缺点：计算成本极高，不适用于大规模网络

2. 变分推断（Variational Inference, VI）

思想：用简单分布 qθ(w)qθ(w)（如高斯族）近似复杂后验 P(w∣D)P(w∣D)
优化目标：最小化变分分布与真实后验的KL散度 → 最大化证据下界（ELBO）：
ELBO=Eqθ(w)[log⁡P(D∣w)]−KL(qθ(w)∥P(w))ELBO=Eqθ(w)[logP(D∣w)]−KL(qθ(w)∥P(w))
实现：
- 贝叶斯层：将神经网络层权重替换为概率分布（如 TensorFlow Probability 中的 DenseVariational 层）
- 重参数化技巧：使梯度可通过随机采样反向传播（如使用高斯分布 N(μ,σ2)N(μ,σ2) 时，采样改为 μ+σ⋅ϵ,ϵ∼N(0,1)μ+σ⋅ϵ,ϵ∼N(0,1)）

3. 蒙特卡洛Dropout（MC Dropout）

惊人发现（Gal & Ghahramani, 2016）：在神经网络中应用Dropout训练等价于贝叶斯推断的近似！
操作：
1. 训练时开启Dropout（作为随机正则化）
2. 预测时也开启Dropout，运行多次（如100次）得到预测分布
优势：只需修改预测代码，成本极低

四、预测：不确定性量化

BNN 的预测是概率分布而非单点值：

输入样本 x∗x∗
采样 TT 组权重：wt∼P(w∣D)(t=1,...,T)wt∼P(w∣D)(t=1,...,T)
计算 TT 个预测：y^t=fwt(x∗)y^t=fwt(x∗)
生成预测分布：
- 均值：最终预测结果 1T∑y^tT1∑y^t
- 方差：不确定性估计（方差越大，置信度越低）

python

# MC Dropout 预测示例（PyTorch）
model.train()  # 预测时保持Dropout开启！
predictions = [model(x_test) for _ in range(100)]
mean_pred = torch.stack(predictions).mean(dim=0)
uncertainty = torch.stack(predictions).std(dim=0)

五、核心优势与应用场景

优势：

不确定性感知：识别分布外样本（OOD）、对抗样本
小数据高效学习：避免过拟合（如医疗影像诊断）
模型压缩：通过权重的后验分布可修剪冗余参数
决策可解释性：提供置信区间（如自动驾驶中的安全决策）

应用场景：

领域	案例
医疗诊断	对低置信度预测要求医生复核（如病理切片分类）
自动驾驶	在恶劣天气下提高不确定性阈值，触发人工接管
金融风控	拒绝对高不确定性贷款申请进行自动审批
科学发现	在实验成本高的领域（如药物研发），优化主动学习样本选择

六、挑战与前沿方向

计算效率
- 变分推断的精度与速度权衡
- 分布式贝叶斯训练（如SWAG, Deep Ensemble变体）
后验分布表达力
- 复杂后验建模（如归一化流、扩散模型替代简单高斯分布）
与Transformer结合
- 贝叶化大语言模型（如BayesFormer）提升鲁棒性
硬件支持
- 针对随机权重优化的AI芯片（如IBM的贝叶斯计算单元）

七、关键代码工具

python

# 工具库推荐
import tensorflow_probability as tfp    # TensorFlow Probability
import pyro                            # Pyro（基于PyTorch）
import pymc3                           # PyMC3（概率编程）

# 示例：用TensorFlow Probability构建贝叶斯层
model = tf.keras.Sequential([
    tfp.layers.DenseVariational(units=64, 
                               make_posterior_fn=tfp.layers.default_mean_field_normal_fn(), 
                               make_prior_fn=tfp.layers.default_multivariate_normal_fn),
    tf.keras.layers.Activation('relu'),
    tfp.layers.DenseVariational(units=10)  # 输出层
])

总结

是什么：贝叶斯神经网络将权重视为随机变量，通过后验分布量化不确定性。
核心价值：输出预测置信度，在安全敏感领域实现可靠决策。
实现路径：
- MCMC（精确但慢）→ 科研用小模型
- 变分推断（精度与效率平衡）→ 工业主流
- MC Dropout（简单高效）→ 快速部署方案
未来：与深度学习、大模型融合，推动AI系统从“预测结果”走向“预测可信度”。