假设检验_ t 检验的例子 2021/12/15_假设检验t检验例题-CSDN博客

参考文档：百度文库里面一些医学实验例子,以及最近外场测试脱网例子

一单个正态总体均值u的 t 检验

1.1 单边

解：

$H_0: u=u_0=72; H_1:u>u_0,\alpha=0.05$

$t=\frac{\bar{x}-u_0}{s/\sqrt{n}} \sim t(n-1)$

# -*- coding: utf-8 -*-
"""
Created on Tue Dec 14 20:45:25 2021

@author: cxf
"""

import numpy as np
from scipy.stats import t 
from enum import IntEnum

class Dirction(IntEnum):   
    LEFT = 1
    RIGHT = 2
    MIDLE = 3

'''
获取下alpha 分位数 
p<alpha
'''
def GetQ(alpha,n,drt):
    
    if drt is Dirction.MIDLE:        
        q = t.isf(alpha/2,n-1)
    elif drt is Dirction.RIGHT:
        q = t.isf(alpha,n-1)
    else:
        q = -t.isf(alpha,n-1)
        
    return q

'''
统计
'''
def Calc():
    u = 72
    x_bar = 74.2
    s = 6.0
    n = 25
    
    z = (x_bar-u)/(s/np.sqrt(n))
    print("\n 计算统计量 %4.3f"%z)
    
    q = GetQ(0.05,n,Dirction.RIGHT)
    print("\n 计算拒绝域 %4.3f"%q)
    
    if z<q:
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立 ")

Calc()

1.2 双边检验

解：

$t=\frac{\bar{x}-u_0}{s/\sqrt{n}} \sim t(n-1)$

# -*- coding: utf-8 -*-
"""
Created on Tue Dec 14 20:45:25 2021

@author: cxf
"""

import numpy as np
from scipy.stats import t 


'''
获取下alpha 分位数 
p<alpha
'''
def GetQ(alpha,n):
    
    q = t.isf(alpha/2,n-1)
    return q

'''
统计
'''
def Calc():
    u1 = 14.1
    x_bar = 14.3
    s = 5.04
    n = 25
    
    z = (x_bar-u1)/(s/np.sqrt(n))
    print("\n 计算统计量 %4.3f"%z)
    
    q = GetQ(0.05,n)
    print("\n 计算拒绝域 %4.3f"%q)
    
    if abs(z)<abs(q):
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立 ")

Calc()
 
 计算统计量 0.198

 计算拒绝域 2.064

 H0假设成立

二基于成对数据的t 检验

2.1: 两款手机脱网到驻网时间测试结果如下：

解：

# -*- coding: utf-8 -*-
"""
Created on Wed Dec 15 09:58:19 2021

@author: chengxf2
"""
import numpy as np
from scipy.stats import t

def GetQ(alpha,n):
    
    q= t.isf(alpha, n-1)
    
    print("\n 下alpha 分位数",round(q,3))
    return q
    
def Calc():
    
    x =[11,50,6,20,70,66,55,46]
    y= [8,10,7,7,15,13,10,6]
    
    
    X = np.array(x)-np.array(y)
    
    x_bar = np.mean(X)
    s = np.std(X,ddof=1)
    n = len(X)
    
    z = x_bar/(s/np.sqrt(n))
    
    print("\n 统计量 ",round(z),"\t 样本个数 ",n,"\t 样本均值 ",round(x_bar,2),"\t 样本方差 ",round(s,3))
    
    q = GetQ(0.05, n)
    
    
    if z>q:
       print("\n H0 不成立:具有统计学差异 u>u_0 ")
    else:
       print("\n H0 成立: 是采样误差导致的")
    
Calc()

2.2 例子2

# -*- coding: utf-8 -*-
"""
Created on Tue Dec 14 20:45:25 2021

@author: cxf
"""

import numpy as np
from scipy.stats import t 
from enum import IntEnum

class Dirction(IntEnum):   
    LEFT = 1
    RIGHT = 2
    MIDLE = 3

'''
获取下alpha 分位数 
p<alpha
'''
def GetQ(alpha,n,drt):
    
    if drt is Dirction.MIDLE:        
        q = t.isf(alpha/2,n-1)
    elif drt is Dirction.RIGHT:
        q = t.isf(alpha,n-1)
    else:
        q = -t.isf(alpha,n-1)
        
    return q

def CalcPair():
    WEIGHT =[490,397,512,401,470,415,431,429,420,275,165,421]
    MINI = [525,415,508,444,500,460,390,432,420,227,268,443]
    
    D= np.array(MINI)- np.array(WEIGHT)
    
    u = np.mean(D)
    s = np.std(D, ddof=1)
    n = len(D)
    
    print("样本均值 %5.3f--样本方差 %5.3f"%(u,s))
    
    z= u/(s/np.sqrt(n))
    print("\n 统计量 %4.2f"%z)
    
    q =GetQ(0.05, n, Dirction.MIDLE)
    
   
    print("\n 计算拒绝域 %4.3f"%q)
    
    if np.abs(z)<np.abs(q):
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立 ")

=======假设H0 成立============

2.3 右边检验例子

def CalcPair():
    #WEIGHT =[490,397,512,401,470,415,431,429,420,275,165,421]
    #MINI = [525,415,508,444,500,460,390,432,420,227,268,443]
    
    dataA = [0.3550, 0.2000, 0.313, 0.363,  0.3544,  0.3450, 0.3050]
    dataB = [0.2755, 0.2545, 0.1800, 0.3230, 0.3113, 0.2955, 0.2870]
    
    D= np.array(dataA)- np.array(dataB)
    
    u = np.mean(D)
    s = np.std(D, ddof=1)
    n = len(D)
    
    print("样本均值 %5.3f--样本方差 %5.3f"%(u,s))
    
    z= u/(s/np.sqrt(n))
    print("\n 统计量 %4.2f"%z)
    
    q =GetQ(0.05, n, Dirction.RIGHT)
    
   
    print("\n 计算拒绝域 %4.3f"%q)
    
    if z<q:
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立 ")

假设H0不成立对照组乳猪组织钙含量高于实验组

三两个正态总体均值差的检验（t检验）

有些研究的设计既不能自身配对，也不便异体配对，而只能把独立的两组相互比较。

例如手术组与非手术组、新药组与对照组。两个样本均数比较的目的在于推断两个样本所代表的两总体均数 $u_1$ 和 $u_2$ 是否相等。

实验设计：

样本符合正态分布，且方差相等（不等做秩和检验）

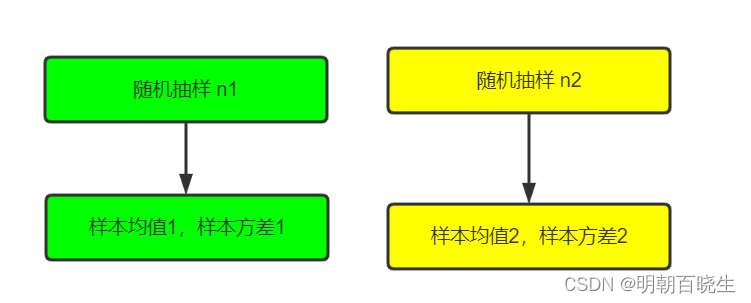
目的：

通过 $\bar{x_1},\bar{x_2}$ 比较 $u_1,u_2$

$H_0 : u_1=u_2, H_1: u_1 \neq u_2,\alpha=0.05$

统计量

$t=\frac{\bar{X_1}-\bar{X_2}}{S_W\sqrt{1/n_1+1/n_2}}$

$s_w^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}$

3.1 例1

例：为了比较国产药和进口药对治疗更年期妇女骨质疏松效果是否相同，采取随机双盲的临床试验方法，评价指标为第2-4腰椎骨密度的改变值。国产药组20例，均数48.25, 标准差32.0；进口药组19例，均数36.37, 标准差27.65。问：两药疗效是否相同？

def TPair():
    n1 = 20
    u1 = 48.25
    s1 =32.0
    
    n2 =19
    u2 =36.37
    s2 = 27.65
    
    n = n1+n2-2
    
    a = u1-u2
    sww = ((n1-1)*np.power(s1,2)+(n2-1)*np.power(s2,2))/(n1+n2-2)
    b = np.sqrt(1/n1+1/n2)
    
    t = a/(np.sqrt(sww)*b)
    print("\n 统计量 %5.3f"%t)
    
    q =GetQ(0.05, n, Dirction.MIDLE)
    
   
    print("\n 计算拒绝域 %4.3f"%q)
    
    if abs(t)<abs(q):
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立")

例 2例某市于1973年和1993抽查部分12岁男童，对其发育情况进行评估，其中身高的有关资料如下，试比较这两个年度12岁男童身高均数有无差别

def TPair():
    n1 = 120
    u1 = 139.9
    s1 = 7.5
    
    n2 =153
    u2 =143.7
    s2 = 6.3
    
    n = n1+n2-2
    
    a = u1-u2
    sww = ((n1-1)*np.power(s1,2)+(n2-1)*np.power(s2,2))/(n1+n2-2)
    b = np.sqrt(1/n1+1/n2)
    
    t = a/(np.sqrt(sww)*b)
    print("\n 统计量 %5.3f"%t)
    
    q =GetQ(0.05, n, Dirction.MIDLE)
    
   
    print("\n 计算拒绝域 %4.3f"%q)
    
    if abs(t)<abs(q):
        
         print("\n H0假设成立 ")
    else:
         print("\n 假设H0不成立")

1973 年：n1=120 `x1 =139.9cm s1=7.5cm；
1993 年：n2=153 `x2 =143.7cm s2=6.3cm

例 某市于1973年和1993抽查部分12岁男童，对其发育情况进行评估，其中身高的有关资料如下，试比较这两个年度12岁男童身高均数有无差别

例 某市于1973年和1993抽查部分12岁男童，对其发育情况进行评估，其中身高的有关资料如下，试比较这两个年度12岁男童身高均数有无差别例 某市于1973年和1993抽查部分12岁男童，对其发育情况进行评估，其中身高的有关资料如下，试比较这两个年度12岁男童身高均数有无差别