前言
本博客先回顾强化学习经典 Monte Carlo 算法,借 Python 实例剖析 Exploring Starts 原理及提升数据效率机制。
大模型训练的过程与强化学习策略迭代在本质上有着惊人的相似性。在大模型训练里,策略评估阶段表现为产生轨迹的过程:将当前输入视为状态(state),模型依据自身策略(模型)生成一个新的词作为动作(action),如此反复,最终生成一个完整的句子,这类似于强化学习中智能体在环境中依据策略行动产生轨迹的过程。而在策略更新阶段,大模型使用精心设计的损失函数,对当前策略进行细致调整与优化,就如同强化学习中根据评估结果改进策略,以期望在未来生成更优质、更符合预期的文本输出。
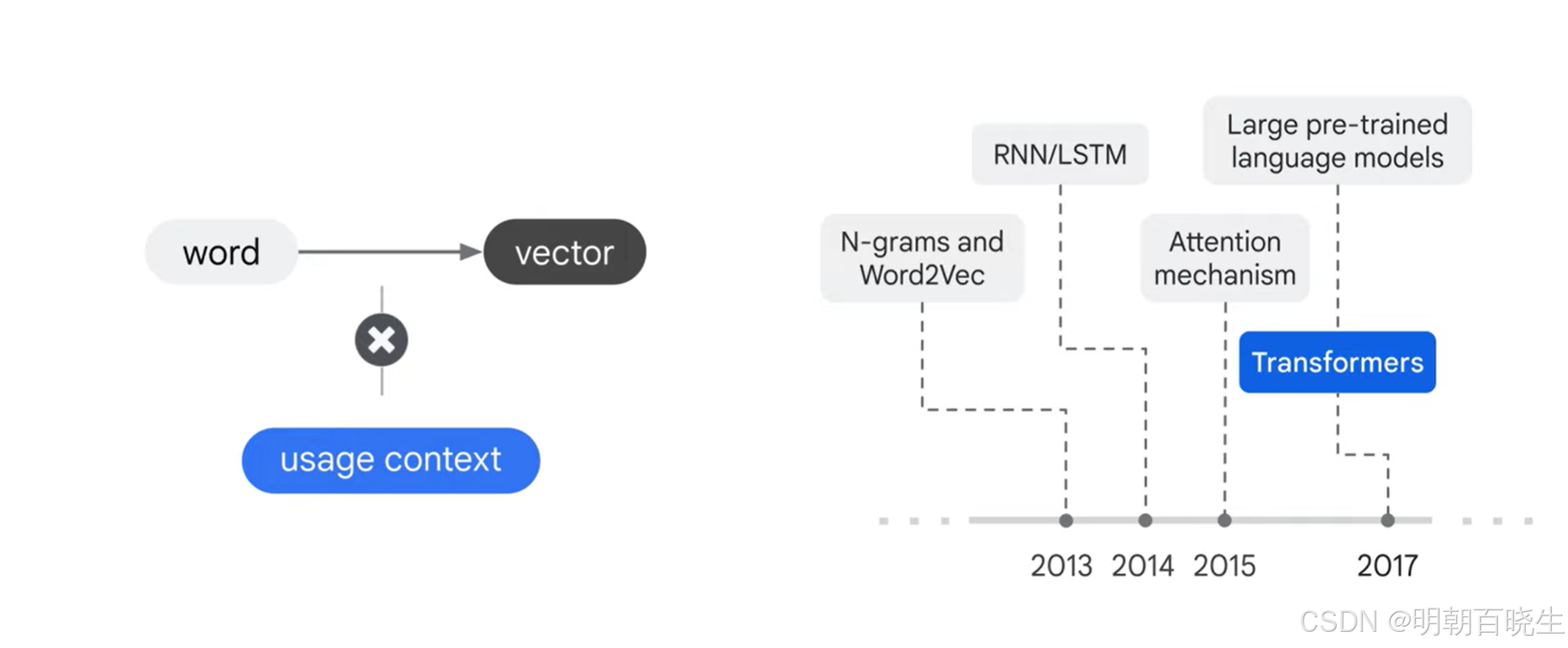
目录:
- Monte Carlo Basic Algorithm
- Monte Carlo Exploring Starts
- Python Implementation Examples for Both Monte Carlo Basic Algorithm and Monte Carlo Exploring Starts
一 MC Basic algorithm
在Model-based RL中,策略迭代(Policy Iteration)的核心流程包括两个关键步骤:
策略评估(Policy Evaluation)
策略改进(Policy Improvement)
核心是计算
,有两种方法:
1: model-based:
2: model-free 定义法:
基于 model-free定义法的策略迭代也就是 MC Basic algorithm

二 MC Exploring starts
1. 数据使用效率(策略评估)
First-visit 方法针对每个状态-动作对,仅记录回合中首次出现时的样本,有效避免同一回合内重复数据对价值估计的影响。
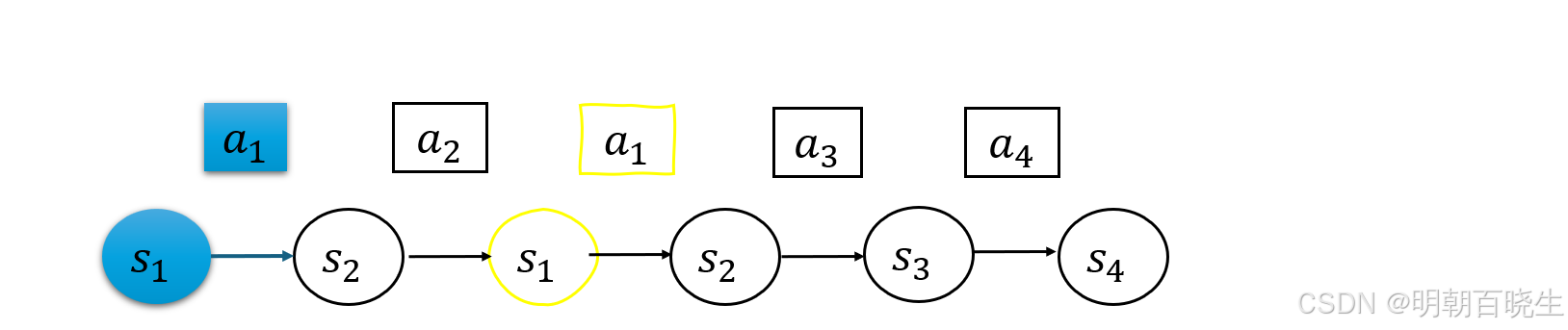
Every-visit 方法统计所有出现时刻的样本,在数据稀缺环境下能够更充分地利用采样信息。
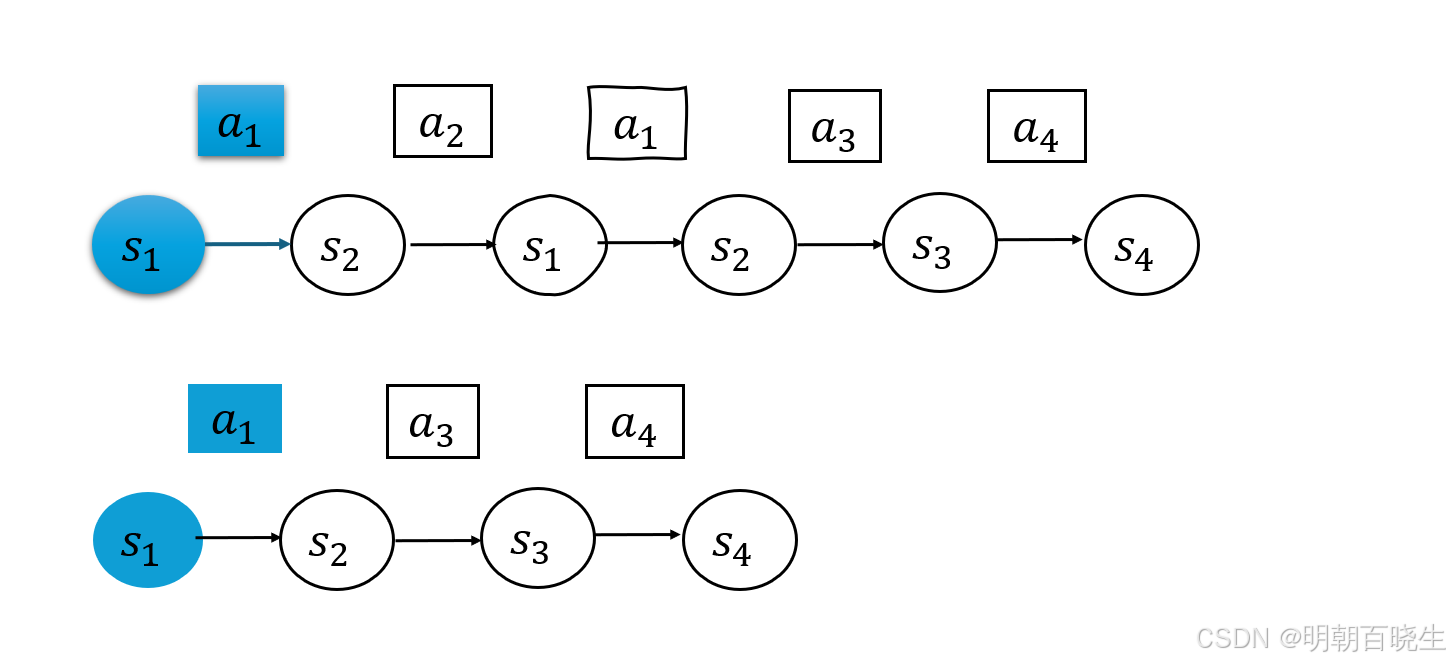
实验结果表明:在样本量不足时,Every-visit方法具有更小的方差;而在大样本条件下,First-visit方法表现出更好的稳定性。
2. 截断采样技术实现
传统MC Basic方法需要对每个状态-动作对采样大量完整回合,计算开销较大。改进方案采用动态截断机制,具体实现如下:
降低episodes_per_state_action的大小,原来计算q(state,action)采样上百个值取均值,
更改为1-2次

3 return 计算效率的提升
-
采用倒序计算方式:
-
其中γ∈(0,1]为折扣因子
-
从终止状态反向计算可避免重复遍历,提升计算效率
-

三 网格世界的例子
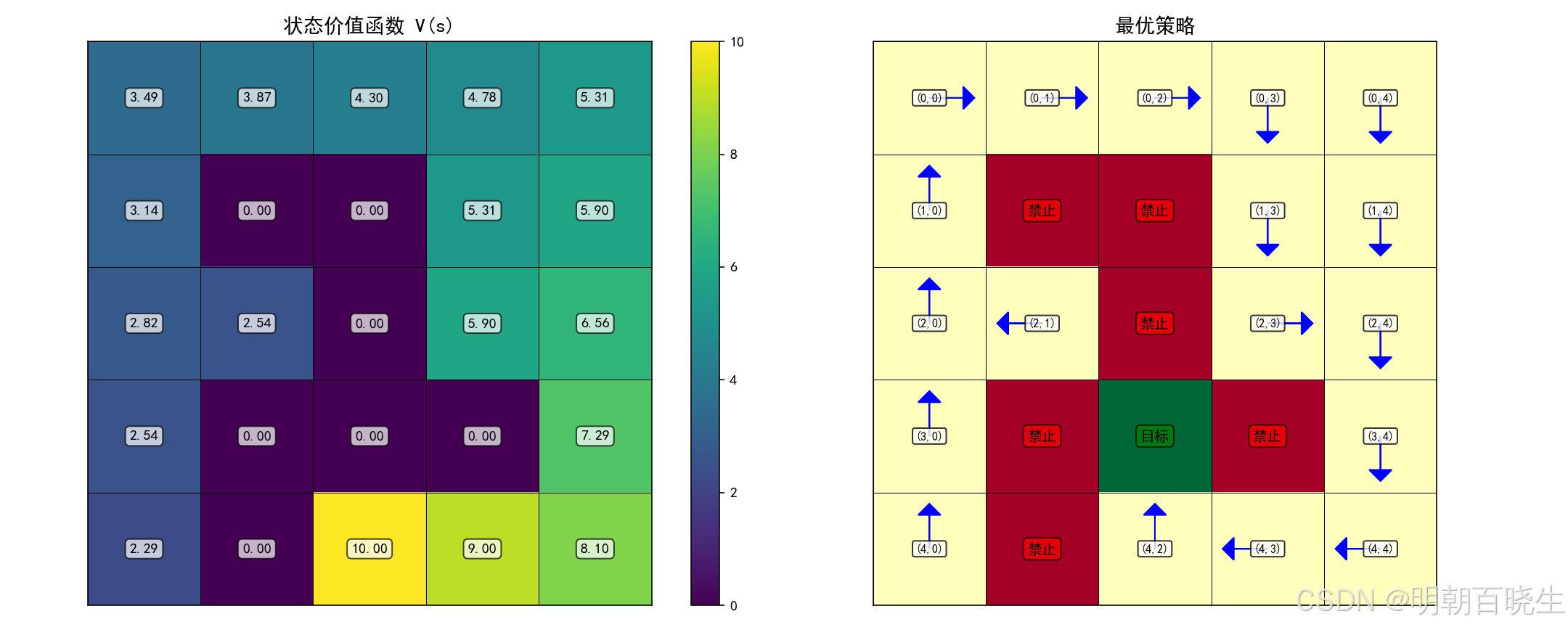
"""
基于MC Basic算法的网格世界强化学习实现
严格遵循策略迭代伪代码结构
作者: chengxf
"""
import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple, List, Dict
import random
from enum import Enum
class DataUsage(Enum):
FIRST_VISIT = 1 #"first-visit"
EVERY_VISIT = 2 #"every-visit"
class CalculationMethod(Enum):
FORWARD = 1 #"forward"
BACKWARD = 2 #"backward"
class GridWorld:
"""5×5网格世界环境"""
def __init__(self):
self.grid_size = (5, 5)
self.rows, self.cols = self.grid_size
# 动作空间
self.actions = [0, 1, 2, 3] # 0:上, 1:下, 2:左, 3:右
self.action_names = ['↑', '↓', '←', '→']
# 奖励设置
self.reward_boundary = -1
self.reward_forbidden = -10
self.reward_target = 10
self.reward_default = 0
# 折扣因子
self.gamma = 0.9
# 特殊状态
self.target_state = (3, 2)
self.forbidden_states = [(1, 1), (1, 2),
(2, 2),
(3, 1), (3, 3),
(4,1)]
# 状态空间
self.states = [(i, j) for i in range(self.rows) for j in range(self.cols)]
self.non_terminal_states = [
s for s in self.states
if s not in self.forbidden_states and s != self.target_state
]
def step(self, state: Tuple[int, int], action: int) -> Tuple[Tuple[int, int], float, bool]:
"""执行动作"""
row, col = state
# 计算下一个状态
if action == 0: # 上
next_state = (max(row - 1,0), col)
elif action == 1: # 下
next_state = (min(row + 1,self.rows - 1), col)
elif action == 2: # 左
next_state = (row, max(col - 1,0))
elif action == 3: # 右
next_state = (row, min( col + 1,self.cols - 1))
else:
raise ValueError(f"无效动作: {action}")
# 检查边界碰撞
hit_boundary = (next_state == state)
# 计算奖励和终止标志
if next_state == self.target_state:
reward = self.reward_target
done = True
elif next_state in self.forbidden_states:
reward = self.reward_forbidden
done = True
elif hit_boundary:
reward = self.reward_boundary
done = False
else:
reward = self.reward_default
done = False
return next_state, reward, done
def is_terminal(self, state: Tuple[int, int]) -> bool:
"""检查是否为终止状态"""
return state == self.target_state or state in self.forbidden_states
class MCBasicAgent:
"""MC Basic算法智能体"""
def __init__(self, env: GridWorld):
self.env = env
self.episode_length = 100
# 初始化随机策略
self.policy = {}
for state in env.non_terminal_states:
# 均匀随机策略
self.policy[state] = {action: 1.0 / len(env.actions) for action in env.actions}
# 动作价值函数
self.q_values = {
state: {action: 0.0 for action in env.actions}
for state in env.non_terminal_states
}
# 记录每个状态-动作对的回报和访问次数
self.returns = {
state: {action: [] for action in env.actions}
for state in env.non_terminal_states
}
# 收敛阈值
self.convergence_threshold = 1e-4
def generate_episode_from_state_action(self, start_state: Tuple[int, int],
start_action: int) -> List[Tuple]:
"""
从特定状态-动作对生成完整回合
参数:
start_state: 起始状态
start_action: 起始动作
返回:
episode: 回合轨迹 [(state, action, reward), ...]
"""
episode = []
state = start_state
action = start_action
# 添加起始状态-动作对(奖励为0,因为尚未执行)
episode.append((state, action, 0))
# 执行起始动作
next_state, reward, done = self.env.step(state, action)
# 更新起始状态-动作对的奖励
episode[-1] = (state, action, reward)
state = next_state
# 继续执行直到终止
while not done and not self.env.is_terminal(state):
# 根据当前策略选择动作
action_probs = self.policy[state]
action = random.choices(
list(action_probs.keys()),
weights=list(action_probs.values())
)[0]
# 执行动作
next_state, reward, done = self.env.step(state, action)
# 记录转移
episode.append((state, action, reward))
state = next_state
# 避免无限循环
if len(episode) > self.episode_length:
break
return episode
def calculate_return(self, episode: List[Tuple],
data_usage: DataUsage = DataUsage.FIRST_VISIT,
calculation_method: CalculationMethod = CalculationMethod.FORWARD) -> float:
"""
计算回合的折扣回报
参数:
episode: 回合轨迹 [(state, action, reward), ...]
data_usage: 数据使用方式 - "first-visit" 或 "every-visit"
calculation_method: 计算方式 - "forward"(正序)或 "backward"(倒序)
返回:
G: 折扣累积回报
"""
if not episode:
return 0.0
# 获取起始状态-动作对(episode的第一个元素)
start_state, start_action, _ = episode[0]
if data_usage is DataUsage.EVERY_VISIT:
# First-visit: 只计算第一次出现的状态-动作对的回报
# 找到该状态-动作对第一次出现的位置
first_occurrence_index = 0
for i, (state, action, _) in enumerate(episode):
if state == start_state and action == start_action:
first_occurrence_index = i
break
# 只从第一次出现的位置开始计算回报
if calculation_method is calculation_method.FORWARD:
# 正序计算:从第一次出现到回合结束
G = 0.0
discount = 1.0
for i in range(first_occurrence_index, len(episode)):
_, _, reward = episode[i]
G += discount * reward
discount *= self.env.gamma
return G
else: # backward
# 倒序计算:从回合结束反向计算到第一次出现
next_return = 0.0
# 从回合末尾向前计算到第一次出现的位置
for i in range(len(episode) - 1, first_occurrence_index - 1, -1):
_, _, reward = episode[i]
current_return = reward + self.env.gamma * next_return
next_return = current_return
if i == first_occurrence_index:
return current_return
return 0.0
else: # every-visit
# Every-visit: 计算所有出现的状态-动作对的平均回报
total_return = 0.0
visit_count = 0
# 找到所有该状态-动作对出现的位置
occurrence_indices = []
for i, (state, action, _) in enumerate(episode):
if state == start_state and action == start_action:
occurrence_indices.append(i)
visit_count += 1
if visit_count == 0:
return 0.0
# 对每个出现的位置计算回报
for idx in occurrence_indices:
if calculation_method == calculation_method.FORWARD:
# 正序计算
G = 0.0
discount = 1.0
for i in range(idx, len(episode)):
_, _, reward = episode[i]
G += discount * reward
discount *= self.env.gamma
total_return += G
else: # backward
# 倒序计算
next_return = 0.0
for i in range(len(episode) - 1, idx - 1, -1):
_, _, reward = episode[i]
current_return = reward + self.env.gamma * next_return
next_return = current_return
if i == idx:
total_return += current_return
# 返回平均回报
return total_return / visit_count
def policy_evaluation(self, episodes_per_state_action: int = 100,
data_usage: DataUsage = DataUsage.FIRST_VISIT,
calculation_method: CalculationMethod = CalculationMethod.FORWARD) -> float:
"""
策略评估:估计所有状态-动作对的价值函数
参数:
episodes_per_state_action: 每个状态-动作对收集的回合数
data_usage: 数据使用方式 - "first-visit" 或 "every-visit"
calculation_method: 计算方式 - "forward" 或 "backward"
返回:
max_value_change: 价值函数的最大变化量
"""
max_value_change = 0.0
# 对每个非终止状态
for state in self.env.non_terminal_states:
# 对每个动作
for action in self.env.actions:
# 清空之前的回报记录
self.returns[state][action] = []
# 收集足够多的回合
for _ in range(episodes_per_state_action):
episode = self.generate_episode_from_state_action(state, action)
# 计算回报,使用指定的数据使用方式和计算方式
G = self.calculate_return(
episode,
data_usage=data_usage,
calculation_method=calculation_method
)
# 记录回报
self.returns[state][action].append(G)
# 计算平均回报作为Q值估计
old_q_value = self.q_values[state][action]
if self.returns[state][action]:
self.q_values[state][action] = np.mean(self.returns[state][action])
# 记录最大变化
value_change = abs(self.q_values[state][action] - old_q_value)
max_value_change = max(max_value_change, value_change)
return max_value_change
def policy_improvement(self) -> bool:
"""
策略改进:基于Q值贪婪地改进策略
返回:
policy_changed: 策略是否发生改变
"""
policy_changed = False
for state in self.env.non_terminal_states:
# 找到最优动作
best_action = None
best_value = -float('inf')
for action in self.env.actions:
if self.q_values[state][action] > best_value:
best_value = self.q_values[state][action]
best_action = action
# 更新策略为确定性策略
new_state_policy = {a: 0.0 for a in self.env.actions}
new_state_policy[best_action] = 1.0
# 检查策略是否改变
if new_state_policy != self.policy[state]:
policy_changed = True
self.policy[state] = new_state_policy
return policy_changed
def policy_iteration(self, max_iterations: int = 100,
episodes_per_state_action: int = 10,
data_usage: DataUsage = DataUsage.FIRST_VISIT,
calculation_method: CalculationMethod = CalculationMethod.FORWARD) -> None:
"""
策略迭代主循环
严格遵循伪代码结构:
while the value estimate has not converged, for kth iteration, do
for every state s in S, do
for every action a in A, do
Collect sufficiently many episodes starting from (s,a) following π_k
q_π_k(s,a) = average return of all episodes starting from (s,a)
# policy improvement steps:
a_k(s) = argmax_a q_π(s,a)
π_{k+1}(a|s) = 1 if a = a_k(s) else 0
"""
print("开始MC Basic策略迭代...")
print(f"数据使用方式: {data_usage}")
print(f"计算方式: {calculation_method}")
iteration = 0
value_converged = False
while iteration < max_iterations and not value_converged:
print(f"\n--- 第 {iteration + 1} 次迭代 ---")
# 策略评估
max_value_change = self.policy_evaluation(
episodes_per_state_action,
data_usage=data_usage,
calculation_method=calculation_method
)
print(f"策略评估完成, 最大价值变化: {max_value_change:.6f}")
# 检查价值函数是否收敛
if max_value_change < self.convergence_threshold:
value_converged = True
print("价值函数已收敛")
# 策略改进
policy_changed = self.policy_improvement()
print(f"策略改进完成, 策略改变: {policy_changed}")
# 显示当前迭代结果
self._display_iteration_results(iteration)
iteration += 1
# 如果策略稳定也可以提前终止
if not policy_changed and value_converged:
print("策略和价值函数均已收敛,终止迭代")
break
def get_deterministic_policy(self) -> Dict[Tuple[int, int], int]:
"""获取确定性策略表示"""
det_policy = {}
for state, action_probs in self.policy.items():
for action, prob in action_probs.items():
if prob > 0.5: # 概率大于0.5认为是选择的动作
det_policy[state] = action
break
return det_policy
def _display_iteration_results(self, iteration: int) -> None:
"""显示当前迭代结果"""
det_policy = self.get_deterministic_policy()
print(f"\n迭代 {iteration + 1} 策略:")
for i in range(self.env.rows):
row_str = ""
for j in range(self.env.cols):
state = (i, j)
if state in det_policy:
action_name = self.env.action_names[det_policy[state]]
row_str += f"({i},{j}):{action_name} "
else:
if state == self.env.target_state:
row_str += " 目标 "
elif state in self.env.forbidden_states:
row_str += " 禁止 "
else:
row_str += " "
#print(f" {row_str}")
def visualize_results(self) -> None:
"""可视化最终结果"""
det_policy = self.get_deterministic_policy()
# 创建价值函数网格
value_grid = np.zeros(self.env.grid_size)
for state in self.env.states:
if state in self.q_values:
# 取最大Q值作为状态价值
value_grid[state] = max(self.q_values[state].values())
# 绘制结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# 价值函数热图
im = ax1.imshow(value_grid, cmap='viridis', interpolation='nearest')
ax1.set_title('状态价值函数 V(s)', fontsize=14, fontweight='bold')
plt.colorbar(im, ax=ax1)
# 添加价值文本
for i in range(self.env.rows):
for j in range(self.env.cols):
ax1.text(j, i, f'{value_grid[i, j]:.2f}',
ha='center', va='center', fontweight='bold',
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.7))
# 策略可视化
grid = np.zeros(self.env.grid_size)
for state in self.env.forbidden_states:
grid[state] = -1
grid[self.env.target_state] = 1
ax2.imshow(grid, cmap='RdYlGn', interpolation='nearest')
ax2.set_title('最优策略', fontsize=14, fontweight='bold')
# 添加策略箭头
for state, action in det_policy.items():
i, j = state
if action == 0: # 上
ax2.arrow(j, i, 0, -0.3, head_width=0.2, head_length=0.1, fc='blue', ec='blue')
elif action == 1: # 下
ax2.arrow(j, i, 0, 0.3, head_width=0.2, head_length=0.1, fc='blue', ec='blue')
elif action == 2: # 左
ax2.arrow(j, i, -0.3, 0, head_width=0.2, head_length=0.1, fc='blue', ec='blue')
elif action == 3: # 右
ax2.arrow(j, i, 0.3, 0, head_width=0.2, head_length=0.1, fc='blue', ec='blue')
ax2.text(j, i, f'({i},{j})', ha='center', va='center',
fontsize=8, fontweight='bold',
bbox=dict(boxstyle="round,pad=0.2", facecolor="white", alpha=0.8))
# 标记特殊状态
for state in self.env.forbidden_states:
i, j = state
ax2.text(j, i, '禁止', ha='center', va='center',
fontweight='bold', fontsize=10,
bbox=dict(boxstyle="round,pad=0.3", facecolor="red", alpha=0.7))
i, j = self.env.target_state
ax2.text(j, i, '目标', ha='center', va='center',
fontweight='bold', fontsize=10,
bbox=dict(boxstyle="round,pad=0.3", facecolor="green", alpha=0.7))
# 添加网格线
for ax in [ax1, ax2]:
for i in range(self.env.rows + 1):
ax.axhline(i - 0.5, color='black', linewidth=0.5)
for j in range(self.env.cols + 1):
ax.axvline(j - 0.5, color='black', linewidth=0.5)
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
plt.show()
# 打印详细Q值表
print("\n详细Q值表:")
for state in self.env.non_terminal_states:
q_str = ", ".join([f"{self.env.action_names[a]}: {self.q_values[state][a]:.3f}"
for a in self.env.actions])
print(f"状态 {state}: {q_str}")
def main():
"""主函数"""
# 创建环境和智能体
env = GridWorld()
agent = MCBasicAgent(env)
# 运行策略迭代,可以尝试不同的数据使用方式和计算方式
agent.policy_iteration(
max_iterations=100,
episodes_per_state_action=10,
data_usage=DataUsage.EVERY_VISIT, # 可以改为 "every-visit"
calculation_method= CalculationMethod.BACKWARD # 可以改为 "backward"
)
# 可视化结果
agent.visualize_results()
if __name__ == "__main__":
main()




















 920
920

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








