Clark变换与Park(派克)变换

最新推荐文章于 2025-03-31 12:17:25 发布

小猫小鱼干

最新推荐文章于 2025-03-31 12:17:25 发布

阅读量10w+

点赞数 83

分类专栏：自学文章标签：电力系统

本文链接：https://blog.csdn.net/chenjianbo88/article/details/53027298

版权

自学专栏收录该内容

29 篇文章

订阅专栏

本文介绍了Clark变换和Park变换的基本原理及其应用。Clark变换用于将三相静止坐标系下的信号转换为两相静止坐标系；Park变换则进一步将信号从两相静止坐标系转换到同步旋转坐标系。文中还提供了变换矩阵的具体形式及逆变换过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

clark变换：将abc 变换到静止的 $\alpha \beta$ 坐标系下。
Park变换：将abc 变换到旋转的 $dq$ 坐标系下。

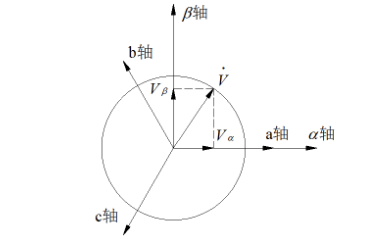
这里写图片描述
记三相对称电压如下：

U a = U b = U c = V m cos ω t V m cos (ω t - 2 3 π) V m cos (ω t + 2 3 π)

$\begin{aligned}U_{a}=&V_{m}\cos \omega t\\ U_{b}=&V_{m}\cos \left(\omega t-{\frac {2}{3}}\pi \right)\\U_{c}=&V_{m}\cos \left(\omega t+{\frac {2}{3}}\pi \right)\end{aligned}$

如图所示，将它们投影到 $\alpha \beta$ 轴上，有：

Clark transformation $3s-2s$ （仅考虑三相三线制情形，零序分量被忽略，详细推导可参考陈伯时《电力拖动自动控制系统-运动控制系统》第三版 P263）

[U α U β] = m * [10 - 1 2 3 \sqrt 2 - 1 2 - 3 \sqrt 2] ⎡ ⎣ ⎢ U a U b U c ⎤ ⎦ ⎥

$\begin{bmatrix} U_{\alpha }\\ U_{\beta } \end{bmatrix} =m*\begin{bmatrix} 1 &-\frac{1}{2} &-\frac{1}{2} \\ 0&\frac{\sqrt{3}}{2} &-\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} U_{a}\\ U_{b}\\ U_{c} \end{bmatrix}$
若

m=23−−√ m = 2 3 $m=\sqrt\frac{2}{3}$ ,变换前后，功率不变。又称为： Concordia变换
若

m=23 m = 2 3 $m=\frac{2}{3}$ , 变换前后，幅值不变。

Inverse Clark transformation $2s-3s$

⎡ ⎣ ⎢ U a U b U c ⎤ ⎦ ⎥ = m' ⎡ ⎣ ⎢ ⎢ ⎢ 1 - 1 2 - 1 2 0 3 \sqrt 2 - 3 \sqrt 2 ⎤ ⎦ ⎥ ⎥ ⎥ [U α U β]

$\begin{bmatrix} U_{a}\\ U_{b}\\ U_{c} \end{bmatrix} =m^{'} \begin{bmatrix} 1 &0 \\ -\frac{1}{2}&\frac{\sqrt3}{2} \\ -\frac{1}{2}& -\frac{\sqrt3}{2} \end{bmatrix} \begin{bmatrix} U_{\alpha }\\ U_{\beta } \end{bmatrix}$

若 $m^{'}=\sqrt\frac{2}{3}$ ,变换前后，功率不变。
若 $m^{'}=1$ ,变换前后，幅值不变。

Park transformation 3s-3r
恒幅值：

⎡ ⎣ ⎢ U d U q U 0 ⎤ ⎦ ⎥ = 2 3 * ⎡ ⎣ ⎢ c o s θ - s i n (θ) 1 / 2 c o s (θ - 2 π / 3) - s i n (θ - 2 π / 3) 1 / 2 c o s (θ + 2 π / 3) - s i n (θ + 2 π / 3) 1 / 2 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ U a U b U c ⎤ ⎦ ⎥

$\begin{bmatrix} U_{d }\\ U_{q}\\ U_{0 } \end{bmatrix} =\frac{2}{3}*\begin{bmatrix} cos\theta &cos(\theta -2\pi/3) &cos(\theta +2\pi/3) \\ -sin(\theta )&-sin(\theta -2\pi/3) &-sin(\theta +2\pi/3)\\ 1/2& 1/2& 1/2 \end{bmatrix} \begin{bmatrix} U_{a}\\ U_{b}\\ U_{c} \end{bmatrix}$

inverse Park transformation 3r-3s
恒幅值：

⎡ ⎣ ⎢ U a U b U c ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ c o s θ c o s (θ - 2 π / 3) c o s (θ + 2 π / 3) - s i n (θ) - s i n (θ - 2 π / 3) - s i n (θ + 2 π / 3) 111 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ U d U q U 0 ⎤ ⎦ ⎥

$\begin{bmatrix} U_{a }\\ U_{b}\\ U_{c } \end{bmatrix} =\begin{bmatrix} cos\theta & -sin(\theta )&1 \\ cos(\theta -2\pi/3)&-sin(\theta -2\pi/3) &1\\ cos(\theta +2\pi/3) &-sin(\theta +2\pi/3) & 1 \end{bmatrix} \begin{bmatrix} U_{d}\\ U_{q}\\ U_{0} \end{bmatrix}$

从Clark变换到Park变换，可由一个旋转变换连接：