简介:
Clark变换主要用于将三相静止系统转换为两相静止系统,简化电机的稳态分析和控制;而Park变换则主要用于将三相静止系统转换为两相旋转系统,实现电机的动态解耦控制。在实际应用中,这两种变换方法通常结合使用,例如在电机的矢量控制中,先通过Clark变换将三相系统转换为两相静止系统,再通过Park变换将两相静止系统转换为两相旋转系统,从而实现对电机的高性能控制。
一、三相坐标(ABC)下的量
以三相坐标下的电压量为例,其中Vm=2VrmsV_m=\sqrt2 V_{rms}Vm=2Vrms,三者之间的关系如下所示:
VA=Vmcos(ωt)VB=Vmcos(ωt−120∘)VC=Vmcos(ωt+120∘)
\begin{align*}
V_A &= V_m \cos(\omega t) \\
V_B &= V_m \cos(\omega t - 120^\circ) \\
V_C &= V_m \cos(\omega t + 120^\circ)
\end{align*}
VAVBVC=Vmcos(ωt)=Vmcos(ωt−120∘)=Vmcos(ωt+120∘)
将三个电压量放在平面的矢量图上,可以更清醒地看出三者之间的关系:
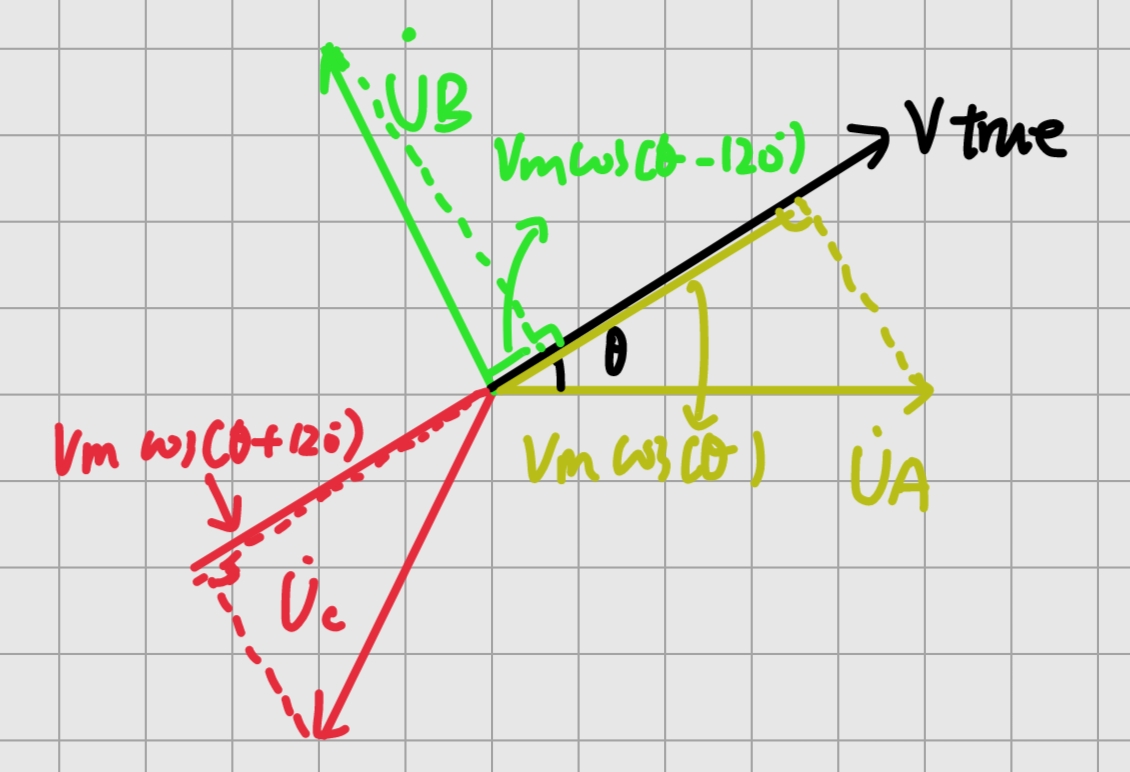
不妨我们这么来理解:黑线,也就是ωt=θ\omega t=\thetaωt=θ对应的矢量是三相电压对应的“真实电压量",A,B,C三相对应的电压量 VA,VB,VCV_A ,V_B ,V_CVA,VB,VC是“真实电压量”在三个坐标下的分别的投影。
那么这个"真实电压量"应该如何计算?利用一个小算子ej120°e^{j120\degree}ej120°,把这个量转化到以A坐标为横坐标,三相坐标原点为坐标原点,过原点,相对于A坐标垂直向上的线为纵坐标,将三相坐标转化到复坐标中,具体计算过程如下所示(自己动手计算一下,利用积化和差与和差化积,计算之后印象更深刻):
Vtrue=VA+VB⋅ej⋅120∘+VC⋅e−j⋅120∘=Vmcos(ωt)+Vmcos(ωt−120∘)⋅ej⋅120∘+Vmcos(ωt+120∘)⋅e−j⋅120∘=Vmcos(ωt)+Vmcos(ωt−120∘)⋅[cos(120∘)+jsin(120∘)]+Vmcos(ωt+120∘)⋅[cos(120∘)−jsin(120∘)]=Vm{cos(ωt)+2cos(ωt)cos(120∘)⋅cos(120∘)+jsin(120∘)⋅2sin(ωt)sin(120∘)}=Vm[32cos(ωt)+j32sin(ωt)]=32Vm⋅ejωt
\begin{align*}V_{true} &= V_A + V_B \cdot e^{j \cdot 120^\circ} + V_C \cdot e^{-j \cdot 120^\circ} \\&= V_m \cos(\omega t) + V_m \cos(\omega t - 120^\circ) \cdot e^{j \cdot 120^\circ} + V_m \cos(\omega t + 120^\circ) \cdot e^{-j \cdot 120^\circ}\\&= V_m \cos(\omega t) + V_m \cos(\omega t - 120^\circ) \cdot [\cos(120^\circ) + j \sin(120^\circ)] + V_m \cos(\omega t + 120^\circ) \cdot [\cos(120^\circ) - j \sin(120^\circ)] \\&= V_m \left\{ \cos(\omega t) + 2 \cos(\omega t) \cos(120^\circ) \cdot \cos(120^\circ) + j \sin(120^\circ) \cdot 2 \sin(\omega t) \sin(120^\circ) \right\} \\&= V_m \left[ \frac{3}{2} \cos(\omega t) + j \frac{3}{2} \sin(\omega t) \right] \\&= \frac{3}{2} V_{m} \cdot e^{j \omega t}\end{align*}
Vtrue=VA+VB⋅ej⋅120∘+VC⋅e−j⋅120∘=Vmcos(ωt)+Vmcos(ωt−120∘)⋅ej⋅120∘+Vmcos(ωt+120∘)⋅e−j⋅120∘=Vmcos(ωt)+Vmcos(ωt−120∘)⋅[cos(120∘)+jsin(120∘)]+Vmcos(ωt+120∘)⋅[cos(120∘)−jsin(120∘)]=Vm{cos(ωt)+2cos(ωt)cos(120∘)⋅cos(120∘)+jsin(120∘)⋅2sin(ωt)sin(120∘)}=Vm[23cos(ωt)+j23sin(ωt)]=23Vm⋅ejωt
那我们的思路就可以从三相的坐标系中跳脱出来,把它放到一个复坐标中进行讨论,也就是下面的αβ\alpha\betaαβ坐标系。
二、αβ\alpha \betaαβ坐标系下的量
很直接的思路,就是直接把“真实电压量”的实部和虚部进行分解,分别拿出来,对应到αβ\alpha\betaαβ坐标下。直观起见,利用下图中的关系,就可以顺利得到变换矩阵。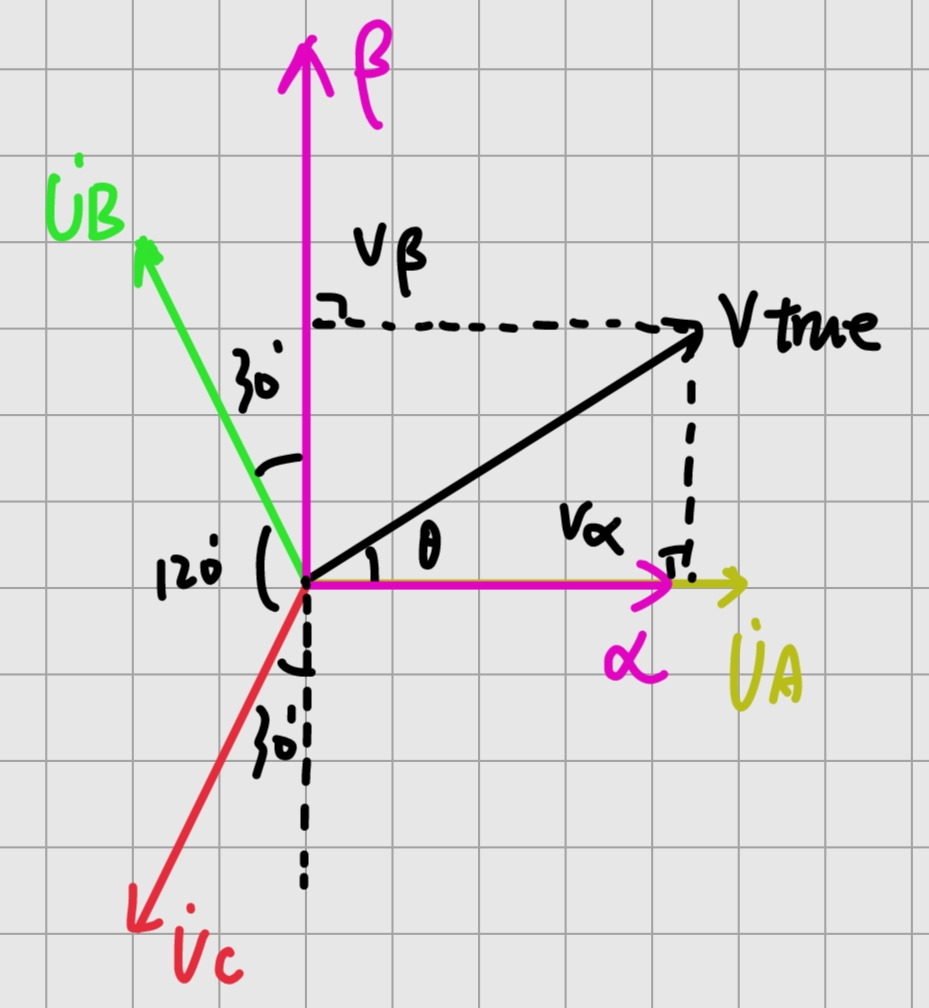
[VαVβ]=[VA−VBcos(60∘)−VCcos(60∘)VBcos(30∘)−VCcos(30∘)]=[1−12−12032−32][VAVBVC]
\begin{bmatrix}V_{\alpha} \\V_{\beta}\end{bmatrix}=\begin{bmatrix}V_A - V_B \cos(60^\circ) - V_C \cos(60^\circ) \\V_B \cos(30^\circ) - V_C \cos(30^\circ)\end{bmatrix}=\begin{bmatrix}1 & -\frac{1}{2} & -\frac{1}{2} \\0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2}\end{bmatrix}\begin{bmatrix}V_A \\V_B \\V_C\end{bmatrix}
[VαVβ]=[VA−VBcos(60∘)−VCcos(60∘)VBcos(30∘)−VCcos(30∘)]=[10−2123−21−23]VAVBVC
当然,也可以直接从VtrueV_{true}Vtrue的表达式中直接推导出这个表达式,请读者自行推导,结果是完全相同的。
则,我们就可以定义变换矩阵,这个变换就叫做Clark变换:
Tabc2αβ=23[1−12−12032−32]
T_{abc2\alpha \beta} = \frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix}
Tabc2αβ=32[10−2123−21−23]
注意:
- 这个变换矩阵,没有考虑零序分量,实际应用中也不用考虑此项;
- 对应的是等幅值变换,因为“真实电压量”是1.5倍的VmV_mVm,为了保持幅值相等需要乘2/3;
- 对于Clark,Park等功率变换的推导,之后博主会更新这篇博客。
三、dq坐标系下的量
为什么要变换到dq坐标系下?
不管是在ABC三相坐标系还是在αβ\alpha\betaαβ坐标系下,所有的量都是交流量,都会随着时间的推移,发生正负大小的变换。
但是如果采用了dq坐标系下的量,交流量可以转化成直流量,对系统的控制会有很大的帮助。
拿最常见的PI控制来讲,PI控制最大的优点就是可以实现对参考值的无净差跟随,如果参考量是交流量,跟随效果就会很差,但是直流系统下的无净差控制就有非常好的效果。
如何理解dq坐标系与αβ\alpha\betaαβ坐标系的关系
两个坐标系的坐标原点重合,时间为0时,d轴与α\alphaα轴重合,q轴与β\betaβ轴重合,唯一的区别,就是dq坐标会绕着坐标原点顺时针转动,而αβ\alpha\betaαβ坐标系保持静止。
这也就体会出来为什么dq坐标系下的交流量是直流量的含义,因为它会随着VtrueV_{true}Vtrue一起转动,VtrueV_{true}Vtrue与dq坐标系两个坐标轴的夹角始终保持一致,那么就会保证dq坐标下的交流量是直流量了。具体数量关系如下图所示:
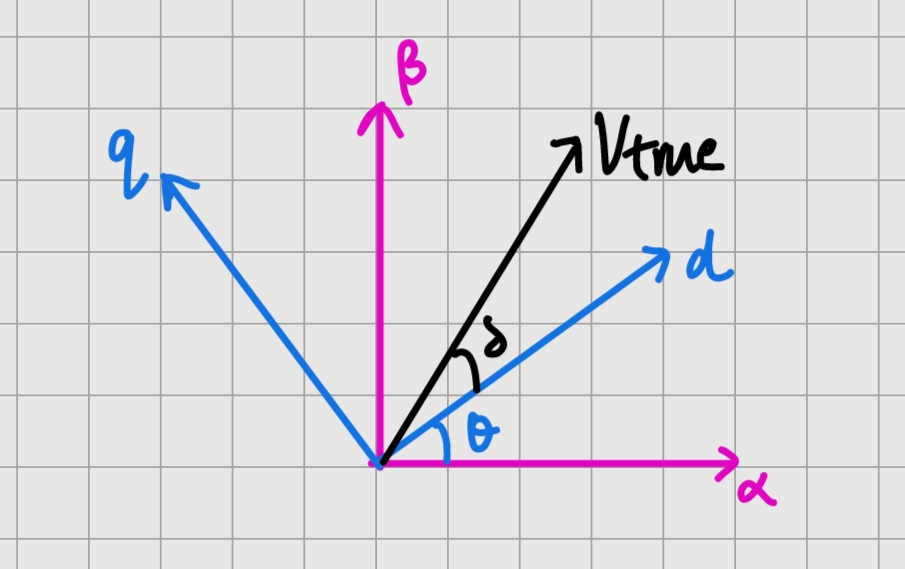
θ\thetaθ就是dq坐标相对于αβ\alpha\betaαβ坐标旋转的角度,δ\deltaδ就是VtrueV_{true}Vtrue相对于d轴的夹角。
{Vα=Vtrue⋅cos(δ+θ)=Vtrue(cosδcosθ−sinδsinθ)Vβ=Vtrue⋅sin(δ+θ)=Vtrue(sinδcosθ+cosδsinθ)Vd=Vtrue⋅cosδVq=Vtrue⋅sinδVd=Vα⋅cosθ+Vβ⋅sinθVq=−Vα⋅sinθ+Vβcosθ
\begin{align*}\begin{cases}V_{\alpha} = V_{\text{true}} \cdot \cos(\delta + \theta) = V_{\text{true}} (\cos \delta \cos \theta - \sin \delta \sin \theta) \\V_{\beta} = V_{\text{true}} \cdot \sin(\delta + \theta) = V_{\text{true}} (\sin \delta \cos \theta + \cos \delta \sin \theta) \\V_d = V_{\text{true}} \cdot \cos \delta \\V_q = V_{\text{true}} \cdot \sin \delta \\V_d = V_{\alpha} \cdot \cos \theta + V_{\beta} \cdot \sin \theta \\V_q = -V_{\alpha} \cdot \sin \theta + V_{\beta} \cos \theta\end{cases}\end{align*}
⎩⎨⎧Vα=Vtrue⋅cos(δ+θ)=Vtrue(cosδcosθ−sinδsinθ)Vβ=Vtrue⋅sin(δ+θ)=Vtrue(sinδcosθ+cosδsinθ)Vd=Vtrue⋅cosδVq=Vtrue⋅sinδVd=Vα⋅cosθ+Vβ⋅sinθVq=−Vα⋅sinθ+Vβcosθ
变换关系如下矩阵所示:
[VdVq]=[Vαcos(θ)+Vβsin(θ)−Vαsin(θ)+Vβcos(θ)]=[cos(θ)sin(θ)−sin(θ)cos(θ)][VαVβ]
\begin{bmatrix}V_d \\V_q\end{bmatrix}=\begin{bmatrix}V_\alpha \cos(\theta) + V_\beta \sin(\theta) \\-V_\alpha \sin(\theta) + V_\beta \cos(\theta)\end{bmatrix}=\begin{bmatrix}\cos(\theta) & \sin(\theta) \\-\sin(\theta) & \cos(\theta)\end{bmatrix}\begin{bmatrix}V_\alpha \\V_\beta\end{bmatrix}
[VdVq]=[Vαcos(θ)+Vβsin(θ)−Vαsin(θ)+Vβcos(θ)]=[cos(θ)−sin(θ)sin(θ)cos(θ)][VαVβ]
我们可以得到变换矩阵,这个变换就叫做Park变换:
Tαβ2dq=[cos(θ)sin(θ)−sin(θ)cos(θ)]
T_{\alpha\beta2dq} = \begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix}
Tαβ2dq=[cos(θ)−sin(θ)sin(θ)cos(θ)]
一个很简单的理解Park变换的小点
借助下面的图片,就很直观地认识到这个计算式:
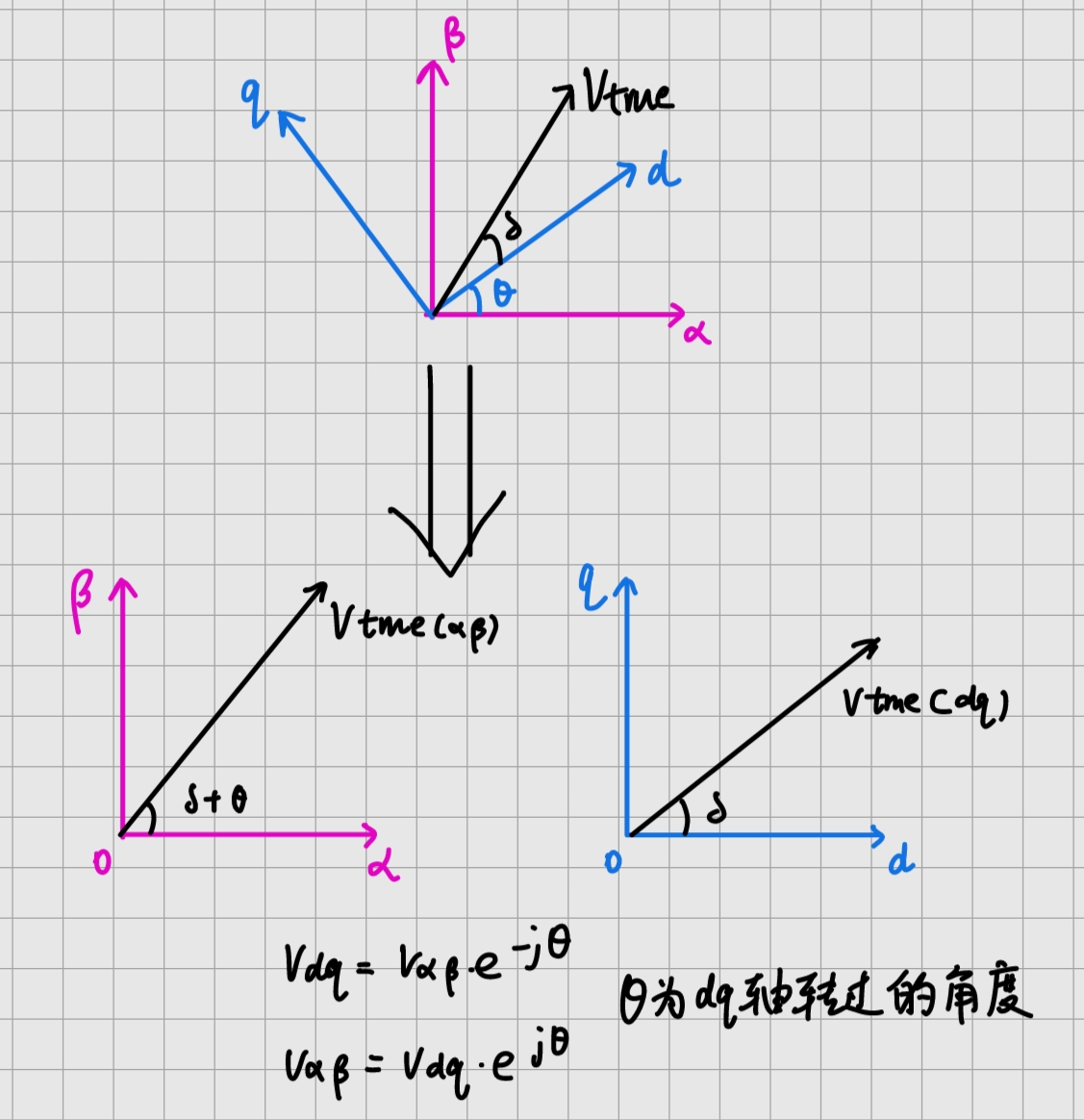
计算式如下所示:
Vα+jVβ=(Vd+jVq)⋅ejθVd+jVq=(Vα+jVβ)⋅e−jθ
V_{\alpha} + j V_{\beta} = (V_d + j V_q) \cdot e^{j \theta}\\
V_{d} + j V_{q} = (V_{\alpha} + j V_{\beta}) \cdot e^{-j \theta}
Vα+jVβ=(Vd+jVq)⋅ejθVd+jVq=(Vα+jVβ)⋅e−jθ
因为这个变换本质就代表着一种旋转关系。
四、等功率变换与不同坐标下的功率计算
未完待续…





















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








