地球围绕着太阳的概念和计算

我受够了含混不清和一知半解，一次找全供大家参考。
出处https://www.pveducation.org/zh-hans/pvcdrom/acknowledgements
1、本地太阳时Local Solar Time LST and Local Time LT
太阳高度角最大时为太阳时的中午十二点。
本地时由世界时和本地时区确定，比如北京时就是 UT+8，UT是Universal Time
2、本地标准时子午线
每360/24=15°，就相差一小时，例如北京时，本地标准子午线在158=120E，东经120°
3、均时差 Equation of Time EoT
EoT=9.87sin（2B）-7.53cosB-1.5sinB
式中 B=360（N-81）/365
N的意思为一年中的第几天，比如1月1号，N=1,2月1号，N=32

4、时间修正系数 TC Time Correction Factor

TC=4*（Longitude-LSTM）+EoT
此处因为每1°相差4分钟，所以TC单位是分钟
5、本地太阳时 LST
LST=LT+TC/60
此处TC除以60，转化为时
比如西安市经度为108.94,2022年3月24日（第83天）的北京时间中午12点，对于本地太阳时相当于
B=360*（83-81）/365 带入EoT，EoT=-6.898单位是分钟

LST=12+（4*（108.94-120）+（-6.898））/60=11.1477即 11点8.862分 差的还挺多的。
6、时角 Hour Angle（HRA）
当太阳时正午时，时角为0°，上午为负，下午为负
HRA=15*(LST-12)
7、赤纬角 Declination Angle
太阳赤纬角是由于地球自转轴倾斜以及地球围绕太阳公转而产生的季节性变化。用δ表示。
赤纬角的计算公式
δ=-23.45cos((360/365)(d+10))
d是一年当中的第几天，相当于前面的N。别忘了前面的负号
也可以用其他的公式代替

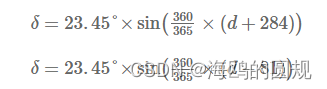
8、太阳高度角Elevation Angle/altitude angle
由于地球赤纬角的存在，一年中某特定时间里太阳的最大高度角（α）是纬度φ和赤纬角δ的函数
α=90+φ-δ
一天中太阳高度角的变化由以下公式获得

9、天顶角 Zenith Angle
ζ=90°-α

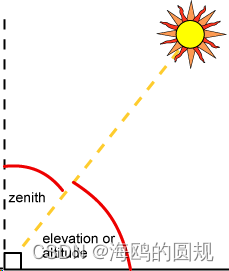
10、日出sunrise和日落sunset

图片里公式COS-1的意思是arccos，一般结算结果为弧度，记得转换成角度。
还是上面那个例子，西安市经度为108.94,纬度为34.26，2022年3月24日（第83天）日出时间和日落时间
3月24日赤纬角为
δ=-23.45cos((360/365)(83+10))=0.70632
TC/60=（4*（108.94-120）+（-6.898））/60=-0.62237
Sunrise=12-arccos(-tgφtgδ)/15-TC/60=6.82相当于北京时间6点49分日出。
sunset=12+arccos(-tgφtgδ)/15-TC/60=18.88438 相当于北京时间18点53分日落
11、方位角 Azimuth Angle
方位角是入射阳光的罗盘方向，在正午时刻，太阳在北半球总是位于正南，在南半球总是位于正北，以与正北方向的夹角为太阳方位角，在春分秋分，太阳日出时方位角为90°，日落时为270°


还是上面那个例子，西安市经度为108.94,纬度为34.26，2022年3月24日（第83天）上午11点和下午4点，太阳方位角分别是
太阳赤纬角δ=-23.45cos((360/365)(83+10))=0.70632°
φ=纬度=34.26°
HRA=15*(LST-12)
当地太阳时LST=11+（4*（108.94-120）+（-6.898））/60=11-0.8523=10.1477
时角HRA=15*（10.1477-12）=-27.7845°
天顶角α=arcsin(sinδsinφ+cosδcosφcosHRA)=0.83023=47.5687°
方位角Azi=arccos（（sinδcosφ-cosδsinφcosHRA）/cosα）=2.378945=136.3035
下午4点的我不算了，太复杂了。