必须认真学习的算法书

最新推荐文章于 2022-01-13 03:33:42 发布

chmodexplorer

最新推荐文章于 2022-01-13 03:33:42 发布

阅读量5.6k

点赞数

文章标签： Algorithm 算法学习纪录

本文链接：https://blog.csdn.net/chmodexplorer/article/details/44657769

版权

章节学习纪录

The Role of Algorithms in Computing 2015-03-26

Getting Started

2.1-1 ~ 2.1-4	2015-03-27	不能大意啊，居然将 INSERTION-SORT 的实现写错了。
2.2-1 ~ 2.2-4	2015-03-28	Decrease-and-Conquer Divide-and-Conquer Transform-and-Conquer
2.3-1 ~ 2.3-7	2015-03-29

Growth of Functions

3.1-1 ~ 3.1-4

2015-03-29

3.1-5 ~ 3.1-7

2015-04-23

3.1-8

We can extend our notation to the case of two parameters n and m that can go to infinity independently at different rates. For a given functiong(n,m), we denote byO(g(n,m)) the set of functions

O(g(n,m)) = {f(n,m) :	there exist positive constants c, n₀, andm₀
	such that 0 ≤ f(n, m) ≤ cg(n, m)
	for all n ≥ n₀ or m≥m₀).

Give corresponding definitions for Ω(g(n,m)) andΘ(g(n,m)).

Pay attention

3.2-1 ~ 3.2-3

2015-05-03

3.2-4

Is the function ⌈lg n⌉! polynomially bounded?
Is the function ⌈lg lg n⌉! polynomially bounded?

No
Yes

3.2-5

Which is asymptotically larger: lg(lg* n) or lg*(lg n)?

lg*(lg n)

3.2-6 ~ 3.2-7

2015-08-05

3.2-8

Show that k lnk = Θ(n) implies k = Θ(n/ln n).
Prove:
c1 n <= k lnk <= c2 n <=> c1 n / lnk <= k <= c2 n / lnk <=> c1 n / lnn < c1 n / lnk <= k

if c1 >= 1,
k lnk >= c1 n => lnk + lnlnk >= lnn => 1 + lnlnk >= lnn / lnk => lnn / lnk <= 1 + lnlnk/lnk < 2,
so there must be a constant c3 -> ( c2 lnn / lnk ) <= c3 => ( c2 n / lnk ) <= ( c3 n / ln n) => k <= ( c3 n / lnn )

if c1 < 1, there must be two constants c4 >= 1, c5 -> c4 n <= c5 k lnk => lnn <= lnc5 + lnk + lnlnk => ......

Rank the following functions by order of growth
30 functions

n^n is always bigger than n!.

Divide-and-Conquer

The Maximum-Profit Problem

4.1

The Maximum-Subarray Problem

how to resolve the problem in O(n) time?

def max_sum_of_subarray_1(A):
    l = len(A)
    assert l > 0
    ms = A[0]
    s = ms   #there is a bug, if s < 0, s must be 0
    i = 1
    while i < l:
        s += A[i]
        if s > ms:
            ms = s
        if s < 0:
            s = 0
        i += 1
    return ms

how to resolve the problem in O(n lgn) time?

def max_sum_of_subarray_1(A):
    l = len(A)
    assert l > 0
    ms = A[0]
    s = ms   #there is a bug, if s < 0, s must be 0
    i = 1
    while i < l:
        s += A[i]
        if s > ms:
            ms = s
        if s < 0:
            s = 0
        i += 1
    return ms

how to resolve the problem in O(n^2) time?

def max_sum_of_subarray_2(A):
    l = len(A)
    assert l > 0
    ms = A[0]
    i = 1
    while i <= l:
        s = A[0]
        j = 1
        while j < i:
            s += A[j]
            j += 1
        if s > ms:
            ms = s
        k = 0
        while j < l:
            s -= A[k]
            s += A[j]
            k += 1
            j += 1
            if s > ms:
                ms = s
        i += 1
    return ms

4.1-1 The return value is negative

4.1-2 max_sum_of_subarray_2

4.1-3 ignore the problem, because the crossover point is nearly useless. The crossover point is changeable.

4.1-4 max_sum_of_subarray_3 does not return the sum of an empty sub-array. If all of the element in the array are negative, and we don't want to return the biggest element, in the case, it is better to return 0, the sum of an empty sub-array. We can modify the code to implement the request in the way: before the last line, we check whether the value of ms is negative, if so, assign 0 to it.

4.1-5 max_sum_of_subarray_1

4.2 Strassen's Algorithm for Matrix Multiplication ignore

4.3-1 ~

4.3-2

2015-08-12

4.3-3 2015-08-13

4.3-4 Show that by making a different inductive hypothesis, we can overcome the difficulty with the boundary conditionT(1) = 1 for recurrence(4.19) without adjusting the boundary conditions for the inductive proof. 2015-8-16

4.3-5 Show that Θ(n lgn) is the solution to the "exact" recurrence(4.3) for merge sort. 2015-8-16

4.3-6 Show that the solution to T(n) = 2T(⌊n/2⌋ + 17) +n isO(n lgn). 2015-8-16

4.3-7

4.3-9

2015-8-16

4.4-1

4.4-4

2015-8-16

4.4-5 Use a recursion tree to determine a good asymptotic upper bound on the recurrenceT(n) =T(n - 1) +T(n/2) +n. Use the substitution method to verify your answer.

Probabilistic Analysis and Randomized Algorithms

5.1-1	What is the total order?	The answer depends on: can we compare any two candidates and then decide which one is best?
5.1-2	n = b - a + 1 O(lg n)	2015-8-17
5.1-3	Pr(P) = p Pr(Q) = 1 - p Pr(PQ) = p (1 - p) Pr(QP) = (1 - p) p	2015-8-17
5.2-1	Pr{hire exactly one time} = (n - 1)! / n! Pr{hire exactly n times} = 1/n!	2015-8-18
5.2-2		2015-8-18
5.2-3	7n/2	2015-8-18
5.2-4	Xi = { the ith customer gets his/her cat back}, why Pr{Xi} = 1/n ?	2015-8-18
5.2-5	(n^2 - n) / 4	2015-8-19
5.3-1		2015-8-30
5.3-2	(n-1)! 种排列	2015-8-30
5.3-3	n^n 种排列	2015-8-30
5.3-4	n 种排列	2015-8-30
5.3-5
5.3-6	1. 使用平衡二叉树记录每个节点（原数组中的值+新的 rank），如果在二叉树中找到相同rank的节点，就重新产生新的rank。直至二叉树最终创建成功。中序遍历，输出节点中原数组中的值，就形成了一个排列。	2015-8-30
5.3-7	n!/(n - m)!	2015-8-31

Heapsort

6.1-1 6.1-2 6.1-3	2015-10-17	[2^h .. 2^(h+1) - 1]
6.1-4	2015-10-17	leaves
6.1-5	2015-10-17	yes
6.1-6	2015-10-17	no
6.1-7 6.2-1 ~ 6.2-6 6.3-1 ~ 6.3-2	2015-10-17
6.3-3 Show that there are at most ⌈n/2^h+1⌉ nodes of heighth in anyn-element heap.
6.4-1 ~ 6.4-4	2015-10-18
6.4-5 Show that when all elements are distinct, the best-case running time of HEAPSORT isΩ(n lgn).	2015-10-18
6.5-1 ~ 6.5-9	2015-10-18	The primary operations of a priority queue are: 1. sink; 2. rise. We can implement other exported functions of priority queue by using the foregoing functions.
Problem 6-1, 6-2	2015-11-05	We can use sink and rise to implement BUILD-MAX-HEAP, and their time complexities are different.
Problem 6-3

quicksort

7.1-1 ~ 7.1-4	2015-10-20
7.2-1 ~ 7.2-4	2015-10-25
7.2-5 Suppose that the splits at every level of quicksort are in the proportion 1 -α toα, where 0 <α≤ 1/2 is a constant. Show that the minimum depth of a leaf in the recursion tree is approximately -lgn/ lgα and the maximum depth is approximately -lgn/ lg(1 -α). (Don't worry about integer round-off.)
7.2-6 Argue that for any constant 0 < α≤ 1/2, the probability is approximately 1 - 2α that on a random input array, PARTITION produces a split more balanced than 1 -α toα.
7.3-1	2015-10-25
7.3-2	2015-10-25	O(n) O(log n)
	2015-10-
	2015-10-
	2015-10-
	2015-10-

Sorting in Linear Time

8.1-1 What is the smallest possible depth of a leaf in a decision tree for a comparison sort?
8.1-2	2015-11-08
8.1-3 Show that there is no comparison sort whose running time is linear for at least half of then! inputs of lengthn. What about a fraction of 1/n of the inputs of lengthn? What about a fraction 1/2ⁿ?
8.1-4	2015-11-08
8.2-1	2015-11-08
8.2-2 Prove that COUNTING-SORT is stable.

8.2-4 Describe an algorithm that, given n integers in the range 0 to k, preprocesses its input and then answers any query about how many of the n integers fall into a range [a ‥ b] in O(1) time. Your algorithm should use Θ(n + k) preprocessing time.
	2015
	2015

Medians and Order Statistics

Elementary Data Structures

10.1-1 ~ 10.1-4	2015-11-21
10.1-5 -- how to implement a double end queue		push_front pop_front push_back pop_back
10.1-6 Show how to implement a queue using two stacks. Analyze the running time of the queue operations.	2015-11-21	Amortized Analysis: O(1)
10.1-7 Show how to implement a stack using two queues. Analyze the running time of the stack operations.	2015-11-21	Amortized Analysis: O(1)
10.2-1	2015-11-21
10.2-2	2015-11-21
10.2-3	2015-11-21	<- 5 <- 4 <- 3 <- 2 <- 1 <- use a singly linked, circular list
10.2-4	2015-11-21
10.2-5	2015-11-22	O(1) O(n) O(n)
10.2-6	2015-11-22	linked list
10.2-7	2015-11-22	insert
10.2-8	2015-11-22	xor
10.3-1 ~ 10.3-3	2015-11-22
10.3.4 It is often desirable to keep all elements of a doubly linked list compact in storage, using, for example, the firstm index locations in the multiple-array representation. (This is the case in a paged, virtual-memory computing environment.) Explain how to implement the procedures ALLOCATE-OBJECT and FREE-OBJECT so that the representation is compact. Assume that there are no pointers to elements of the linked list outside the list itself.
10.3-5	2015-11-25	template <typename T> struct node { node<T> * prev; node<T> * next; bool used; T data; }; template <typename T> void replace(node<T> * from, node<T> * to) { assert(from != NULL && to != NULL && from != to); node<T> * prev = from->prev; node<T> * next = from->next; to->data = from->data; to->used = from->used; if (prev != NULL) { prev->next = to; } to->prev = prev; to->next = next; if (next != NULL) { next->prev = to; } #if (defined(DEBUG) \|\| defined(_DEBUG) \|\| defined(DBG)) from->prev = from->next = NULL; from->data = T(); #endif } template <typename T> node<T> * reorganize(std::vector<node<T>> & buffer, node<T> * head) { node<T> * unused = NULL, dummy = {NULL, NULL, false, T()}; assert(head != NULL); for (size_t i = 0, n = buffer.size(); i < n; ++i) { if (head != NULL) { if (head != &buffer[i]) { if (buffer[i].used) { replace(&buffer[i], &dummy); replace(head, &buffer[i]); replace(&dummy, head); } else { replace(head, &buffer[i]); head->used = false; } } } else { unused = &buffer[i]; break; } head = buffer[i].next; } return unused; }

Hash Tables

11.1-1	2015-11-26	The answer depends on how to translate the value of the element to index, if the maximum value item has the biggest index, the worst-case performance is O(1). Generally it is O(n)
11.1-2, 11.1-3	2015-11-26
11.1-4 We wish to implement a dictionary by using direct addressing on a huge array. At the start, the array entries may contain garbage, and initializing the entire array is impractical because of its size. Describe a scheme for implementing a direct-address dictionary on a huge array. Each stored object should useO(1) space; the operations SEARCH, INSERT, and DELETE should take O(1) time each; and initializing the data structure should take O(1) time. (Hint: Use an additional array, treated somewhat like a stack whose size is the number of keys actually stored in the dictionary, to help determine whether a given entry in the huge array is valid or not.)

Binary Search Trees

12.1-1	2015-11-29
12.1-2	2015-11-29	two differences: 1. BST might be perfect balanced; 2. the minimum item is in the left sub-tree of the root, not in the root node.
12.1-3 ~ 12.1-5	2015-11-29
12.2-1	2015-11-29	c, e
12.2-2 ~ 12.2-3	2015-11-29
12.2-4	2015-11-29	find answer from the question 12.2-1
12.2-5 ~ 12.2-6	2015-11-29
12.2-7 An alternative method of performing an inorder tree walk of an n-node binary search tree finds the minimum element in the tree by calling TREE-MINIMUM and then making n - 1 calls to TREE-SUCCESSOR. Prove that this algorithm runs in Θ(n) time.		why is its performance O(n) to walk through a binary tree: T(n) = T(m) + T(n - m - 1) + c => T(n) <= dn (if d >= c)
12.2-8 Prove that no matter what node we start at in a height-h binary search tree, k successive calls to TREE-SUCCESSOR take O(k + h) time.
12.2-9 Let T be a binary search tree whose keys are distinct, let x be a leaf node, and let y be its parent. Show that y.key is either the smallest key in T larger than x.key or the largest key in T smaller than x.key.	2015-11-29	proof by contradiction
12.3-1 ~ 12.3-3	2015-11-29
12.3-4 Is the operation of deletion "commutative" in the sense that deleting x and then y from a binary search tree leaves the same tree as deleting y and then x? Argue why it is or give a counterexample.	2015-11-29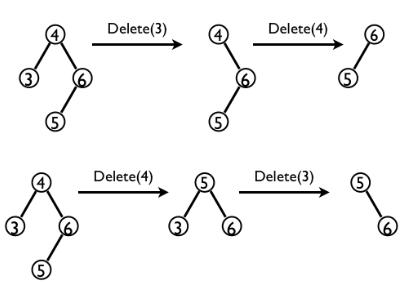
12.3-5 Suppose that instead of each node x keeping the attribute x.p, pointing to x's parent, it keeps x.succ, pointing to x's successor. Give pseudocode for SEARCH, INSERT, and DELETE on a binary search tree T using this representation. These procedures should operate in time O(h), where h is the height of the tree T.
12.3-6 When node z in TREE-DELETE has two children, we could choose node y as its predecessor rather than its successor. What other changes to TREE-DELETE would be necessary if we did so? Some have argued that a fair strategy, giving equal priority to predecessor and successor, yields better empirical performance. How might TREE-DELETE be changed to implement such a fair strategy?
12.4-1	2015-11-29	mathematical induction
12.4-2 Describe a binary search tree on n nodes such that the average depth of a node in the tree is Θ(lg n) but the height of the tree is ω(lg n). Give an asymptotic upper bound on the height of an n-node binary search tree in which the average depth of a node is Θ(lg n).

Red-Black Trees

Lemma 13.1	2015-11-21	n >= 2 ^ bh - 1 => bh <= log(n + 1) h <= 2 bh = 2log(n + 1)
13.1-1 ~ 13.1-5	2015-11-21
13.1-6 What is the largest possible number of internal nodes in a red-black tree with black-height k? What is the smallest possible number?	2015-11-21	[2 ^ k - 1, 2 ^ (2k) - 1]
13.1-7 Describe a red-black tree on n keys that realizes the largest possible ratio of red internal nodes to black internal nodes. What is this ratio? What tree has the smallest possible ratio, and what is the ratio?

Augmenting Data Structures

14.1-1 ~ 14.1-4	2015-12-03	template <typename T> struct binary_tree_node { T data; binary_tree_node<T> * left; binary_tree_node<T> * right; size_t size; }; template <typename T> size_t get_size(binary_tree_node<T> * node) { size_t n = 0; if (node != NULL) { n = node->size; } return n; } template <typename T> binary_tree_node<T> * private_select( binary_tree_node<T> * root, size_t k ) { assert(root != NULL && root->size >= k); binary_tree_node<T> * ret = NULL; for (binary_tree_node<T> * p = root; p != NULL;) { size_t ls = get_size(p->left); if (ls >= k) { p = p->left; } else { size_t r = k - ls; if (r == 1) { ret = p; break; } else { p = p->right; k = r - 1; } } } return ret; } template <typename T> binary_tree_node<T> * select( binary_tree_node<T> * root, size_t k ) { binary_tree_node<T> * ret = NULL; if (root != NULL && root->size >= k) { ret = private_select(root, k); } return ret; } template <typename T> size_t rank_r( binary_tree_node<T> * root, typename boost::call_traits<T>::param_type v ) { size_t ret = SIZE_MAX; if (root != NULL) { if (root->data < v) { size_t inc = get_size(root->left) + 1; size_t rr = rank_r(root->right, v); if (rr < SIZE_MAX) { ret = rr + inc; } } else if (root->data > v) { ret = rank_r(root->left, v); } else { ret = get_size(root->left) + 1; } } return ret; } template <typename T> size_t rank_i( binary_tree_node<T> * root, typename boost::call_traits<T>::param_type v ) { size_t ret = SIZE_MAX, inc = 0; for (binary_tree_node<T> * p = root; p != NULL;) { if (p->data < v) { inc += (get_size(p->left) + 1); p = p->right; } else if (p->data > v) { p = p->left; } else { ret = inc + get_size(p->left) + 1; break; } } return ret; }
14.1-5	2015-12-03	1) r = rand(root, x) 2) nr = r + i 3) select(root, nr)
14.1-6	2015-12-03	It only takes O(1) time to maintain the correct field "size" in each node in those rotation operations.

Dynamic Programming

15.1-1	2015-12-10	T(n) = T(n-1) + T(n-2) + ... + T(1) + T(0) + 1 T(n + 1) = T(n) + T(n-1) + T(n-2) + ... + T(0) + 1 = 2T(n) => T(n) = O(2^n)
15.1-2	2015-12-10
15.1-3	2015-12-11
15.1-4	2015-12-11	from __future__ import print_function def get_price(price_table, i): ret = 0 n = len(price_table) if i < n: ret = price_table[i] return ret def print_solution(cache, n, loss): on = n s = cache[n][1] solution = "" while s != 0: if len(solution) > 0: solution += "," solution += str(s) n = n - s s = cache[n][1] if len(solution) > 0: solution += "," solution += str(n) print("%s(%s): %s => %s" %(on, loss, cache[on][0], solution)) def cut(price_table, n, loss): cache = [[0, 0] for i in range(n + 1)] cache[1] = [get_price(price_table, 1), 0] i = 2 while i <= n: s = 0 v = get_price(price_table, i) j = 1 while j < i: v2 = cache[j][0] + cache[i - j][0] - loss if v < v2: s = j v = v2 j += 1 cache[i] = [v, s] i += 1 print_solution(cache, n, loss) return cache[n][0]
15.1-5	2015-12-10

Greedy Algorithms

Amortized Analysis

B-Trees

Fibonacci Heaps

van Emde Boas Trees

Data Structures for Disjoint Sets

Elementary Graph Algorithms

22.1-1	2015-12-06	O(E)
22.1-2 ~ 22.1-4	2015-12-06
22.1-5
22.1-6
22.1-7
22.1-8
22.2-1 ~ 22.2.-5	2015-12-06
22.2-6	2015-12-06	I guess that the question wants to say: bfs cannot generate all of the short paths from v to w.
22.2-7		distance % 2
22.2-8 The *diameter* of a treeT = (V,E) is defined as max_u,v∈Vδ(u,v), that is, the largest of all shortest-path distances in the tree. Give an efficient algorithm to compute the diameter of a tree, and analyze the running time of your algorithm.
22.2-9 Let G = (V, E) be a connected, undirected graph. Give an O(V +E)-time algorithm to compute a path inG that traverses each edge inE exactly once in each direction. Describe how you can find your way out of a maze if you are given a large supply of pennies.
22.3-1 Make a 3-by-3 chart with row and column labels WHITE, GRAY, and BLACK. In each cell (i,j), indicate whether, at any point during a depth-first search of a directed graph, there can be an edge from a vertex of colori to a vertex of color j. For each possible edge, indicate what edge types it can be. Make a second such chart for depth-first search of an undirected graph.
22.3-2 ~ 22.3-4	2015-12-06
22.3-5 Show that edge (u, v) is a tree edge or forward edge if and only if u.d < v.d < v.f < u.f, a back edge if and only if v.d ≤ u.d < u.f ≤ v.f, and a cross edge if and only if v.d < v.f < u.d < u.f.
22.3-6
22.3-7	2015-12-06	class DepthFirstPaths: def __dfs_r(self, v): self.color[v] = GRAY self.time += 1 self.d[v] = self.time for w in self.graph.adj(v): if self.color[w] == WHITE: self.p[w] = v self.__dfs_r(w) self.time += 1 self.f[v] = self.time self.color[v] = BLACK def __dfs_i(self, v): self.color[v] = GRAY self.time += 1 self.d[v] = self.time p = v stack = [[0, self.graph.adj(v)]] while stack: top = stack[-1] while top[0] < len(top[1]): w = top[1][top[0]] if self.color[w] == WHITE: self.p[w] = p self.color[w] = GRAY self.time += 1 self.d[w] = self.time stack.append([0, self.graph.adj(w)]) p = w top = stack[-1] else: top[0] += 1 stack.pop() if stack: top = stack[-1] w = top[1][top[0]] self.time += 1 self.f[w] = self.time self.color[w] = BLACK top[0] += 1 if len(stack) > 1: p = stack[-2][1][stack[-2][0]] else: p = v def __init__(self, g, s): self.graph = g self.time = 0 v = len(self.graph) self.color = [WHITE for i in range(v)] self.d = [None for i in range(v)] self.f = [None for i in range(v)] self.p = [ -1 for i in range(v)] #self.__dfs_r(s) self.__dfs_i(s) def has_path_to(self, w): return self.color[w] == BLACK def get_path_to(self, w): path = [] if self.has_path_to(w): while w != -1: path.append(w) w = self.p[w] path.reverse() return path
22.3-8	2015-12-08	a: b b: u v u: b If we browse the graph began from a, even there is a path from u to v, but u and v are the children of b in the DFS tree.
22.3-9	2015-12-08
22.3-10	2015-12-08	def dfs_print_edge(g, s, st): st.color[s] = GRAY st.time += 1 st.d[s] = st.time for i in g.adj(s): if st.color[i] == WHITE: print(s, "->", i, " is tree edge") st.p[i] = s dfs_print_edge(g, i, st) elif st.color[i] == GRAY: print(s, "->", i, " is back edge") else: if st.d[s] > st.d[i]: print(s, "->", i, " is cross edge") else: print(s, "->", i, " is forward edge") st.time += 1 st.f[s] = st.time st.color[s] = BLACK def print_edge(g): class St: ... st = St() v = len(g) st.color = [WHITE for i in range(v)] st.time = 0 st.d = [-1 for i in range(v)] st.f = [-1 for i in range(v)] st.p = [-1 for i in range(v)] for i in range(v): if st.color[i] == WHITE: dfs_print_edge(g, i, st) cross edges do not exist for undirected graphs, forward edges either.
22.3-11	2015-12-08	a -> u -> b. 1 b 2 u 3 a => we get a depth-first forest
22.3-12	2015-12-08
22.3-13 A directed graph G = (V,E) is singly connected if u⇝v; implies that G contains at most one simple path from u to v for all vertices u,v∈V. Give an efficient algorithm to determine whether or not a directed graph is singly connected.
22.4-1	2015-12-08
22.4-2	2015-12-19	`def count_path(g, sequence): n = len(sequence) dic = {sequence[i]:i for i in range(n)} cache = [0 for i in range(n)] cache[n - 1] = 1 i = n - 2 while i >= 0: u = sequence[i] count = 0 for v in g.adj(u): p = dic.get(v) if p != None: count += cache[p] cache[i] = count i -= 1 return cache`
22.4-
22.4

Minimum Spanning Trees

Single-Source Shortest Paths

All-Pairs Shortest Paths

Maximum Flow

Multithreaded Algorithms

Matrix Operations

Linear Programming

Algorithms Fourth Edition

章节

学习纪录

Fundamentals

Sorting

Elementary Sorts.

2.1.1 ~ 2.1.15	2015-10-20
2.1.16 Certification. Write a check() method that calls sort() for a given array and returns true if sort() puts the array in order and leaves the same set of objects in the array as were there initially, false otherwise. Do not assume that sort() is restricted to move data only with exch(). You may use Arrays.sort() and assume that it is correct.
2.1.17 Animation. Add code to Insertion and Selection to make them draw the array contents as vertical bars like the visual traces in this section, redrawing the bars after each pass, to produce an animated effect, ending in a “sorted” picture where the bars appear in order of their height. Hint : Use a client like the one in the text that generates random Double values, insert calls to show() as appropriate in the sort code, and implement a show() method that clears the canvas and draws the bars.
2.1.18 Visual trace. Modify your solution to the previous exercise to make Insertion and Selection produce visual traces such as those depicted in this section. Hint : Judicious use of setYscale() makes this problem easy. Extra credit : Add the code necessary to produce red and gray color accents such as those in our figures.
2.1.19 Shellsort worst case. Construct an array of 100 elements containing the numbers 1 through 100 for which shellsort, with the increments 1 4 13 40, uses as large a number of compares as you can find.
2.1.20 ~ 2.1.22	2015-10-20

Mergesort

2.2.1 ~ 2.2.3	2015-10-21
2.2.4 Does the abstract in-place merge produce proper output if and only if the two input subarrays are in sorted order? Prove your answer, or provide a counterexample.
2.2.5	2015-10-21
2.2.6 Write a program to compute the exact value of the number of array accesses used by top-down mergesort and by bottom-up mergesort. Use your program to plot the values for N from 1 to 512, and to compare the exact values with the upper bound 6N lg N.
2.2.7 Show that the number of compares used by mergesort is monotonically increasing (C(N+1) > C(N) for all N > 0).
2.2.8 Suppose that Algorithm 2.4 is modified to skip the call on merge() whenever a[mid] <= a[mid+1]. Prove that the number of compares used to mergesort a sorted array is linear.
2.2.9	2015-10-21

Quicksort

2.3.1 ~ 2.3.2	2015-10-23
2.3.3 What is the maximum number of times during the execution of Quick.sort() that the largest item can be exchanged, for an array of length N ?

Priority Queues

2.4.1

2015-10-23

2.4.2 Criticize the following idea: To implement find the maximum in constant time, why not use a stack or a queue, but keep track of the maximum value inserted so far, then return that value for find the maximum?

2.4.3

data structure	insert	remove the maximum
unordered array	O(1)	O(n)
ordered array	O(n)	O(n)
unordered linked list	O(1)	O(n)
linked list	O(n)	O(1)

2.4.4

Yes

2.4.5

YTUSQNEASIOE

2.4.6

2015-10-23

2.4.7 The largest item in a heap must appear in position 1, and the second largest must be in position 2 or position 3. Give the list of positions in a heap of size 31 where the kth largest

(i) can appear, and

(ii) cannot appear, for k=2, 3, 4 (assuming the values to be distinct).

2.4.8 Answer the previous exercise for the kth smallest item.

Applications

Searching

Symbol Tables

3.1.1 ~ 3.1.3	ignore

Binary Search Trees

3.2.1 ~3.2.3	2015-11-21
3.2.4 -- b, d	2015-11-21

Balanced Search Trees

3.3.1 ~ 3.3.4	2015-11-21
3.3.5 Draw all the structurally different trees for N = 7, 8, 9, and 10.	2015-12-05	7 -> 4 8 -> 5 9 -> 8 10 ->13
3.3.6	2015-12-05	1 -> 100% 2-> 100% 3 -> 100% 4 -> 50% 5 -> 50%
3.3.7 ~ 3.3.8	2015-12-05
3.3.9	2015-12-05	(iii) (iv)
3.3.10 ~ 3.3.11	2015-12-05

Hash Tables

Applications

Graphs

Undirected Graphs

4.1.1	2015-12-05	v(v - 1)/2 v - 1
4.1.2 ~ 4.1.5	2015-12-05

Directed Graphs

Minimum Spanning Trees

Shortest Paths

Introduction to the Design and Analysis of Algorithms (Third Edition)

章节

学习纪录

Exercises 1.1

1 ~ 3	2015-10-5

Programming Pearls (Second Edition)

章节

学习纪录

Column 1

Column 2

Column 3

Column 4

Column 5

Column 6

Column 7

Column 8

Column 9

Column 10

Column 11

1	2015-10-25	1. Mode: 是一组数据中出现次数最多的数值，叫众数 2. Mean: 平均值，平均数 3. median: 中位数
2	2015-10-25	In order to optimize a loop, we may nest a new loop in it with less conditions in the new loop
3		How could you experiment to find the best value of cutoff on a particular system?
4	2015-10-25
5		Show how to use Lomuto's partitioning scheme to sort varying-length bit strings in time proportional to the sum of their length.
6 ~ 14	2015-10-26

Column 12

Column 13

Column 14

Column 15

Foundations of Algorithms, Fourth Edition

章节

学习纪录

1 Algorithms: Efficiency, Analysis, and Order

1. Write an algorithm that finds the largest number in a list (an array) of n numbers.	2015-11-04
2. Write an algorithm that finds the m smallest numbers in a list of n numbers.	2015-11-05	use partition to implement the algorithm
3. Write an algorithm that prints out all the subsets of three elements of a set of n elements. The elements of this set are stored in a list that is the input to the algorithm.	2015-11-05	based on the bit operations
4. Write an Insertion Sort algorithm (Insertion Sort is discussed in Section 7.2) that uses Binary Search to find the position where the next insertion should take place.	2015-11-06
5. Write an algorithm that finds the greatest common divisor of two integers.	2015-11-04
6. Write an algorithm that finds both the smallest and largest numbers in a list of n numbers. Try to find a method that does at most 1.5n comparisons of array items.	2015-11-05
7. Write an algorithm that determines whether or not an almost complete binary tree is a heap.	2015-11-06
8 ~ 9	2015-11-04
10. Define basic operations for your algorithms in Exercises 1-7, and study the performance of these algorithms. If a given algorithm has an every-case time complexity, determine it. Otherwise, determine the worst-case time complexity.
11. Determine the worst-case, average-case, and best-case time complexities for the basic Insertion Sort and for the version given in Exercise 4, which uses Binary Search.
12. Write a Θ(n) algorithm that sorts n distinct integers, ranging in size between 1 and kn inclusive, where k is a constant positive integer. (Hint: Use a kn-element array.)
13.	2015-11-04	8
14. There are two algorithms called Alg1 and Alg2 for a problem of size n. Alg1 runs inn² microseconds and Alg2 runs in 100n logn microseconds. Alg1 can be implemented using 4 hours of programmer time and needs 2 minutes of CPU time. On the other hand, Alg2 requires 15 hours of programmer time and 6 minutes of CPU time. If programmers are paid 20 dollars per hour and CPU time costs 50 dollars per minute, how many times must a problem instance of size 500 be solved using Alg2 in order to justify its development cost.
15 ~ 17	2015-11-05
18. Let p(n) =a_kn^k +a_k_-1n^k^-1 + ⋯ + a₁n +a₀, wherea_k > 0. Show thatp(n)∈Θ(n^k).
19.	2015-11-06
20 ~ 21
22.	2015-11-06
23.
24.	2015-11-06
25.	2015-11-07	impossible
26 ~ 33	2015-11-07
34.	2015-11-07	a. yes b. yes (unless f(n) < 1) c. no
35.	2015-11-07	1. sort first 2. partition
36. Algorithm 1.7 (nth Fibonacci Term, Iterative) is clearly linear in n, but is it a linear-time algorithm? In Section 1.3.1 we defined the input size as the size of the input. In the case of the nth Fibonacci term, n is the input, and the number of bits it takes to encode n could be used as the input size. Using this measure, the size of 64 is lg 64 = 6, and the size of 1,024 is lg 1,024 = 10. Show that Algorithm 1.7 is exponential-time in terms of its input size. Show further that any algorithm for computing the nth Fibonacci term must be an exponential-time algorithm because the size of the output is exponential in the input size. (See Section 9.2 for a related discussion of the input size.)
37. Determine the time complexity of Algorithm 1.6 (nth Fibonacci Term, Recursive) in terms of its input size (see Exercise 34).
38. Can you verify the correctness of your algorithms for Exercises 1 to 7?

2 Divide-and-Conquer

1 ~ 5	2015-11-07
6. Write an algorithm that searches a sorted list of n items by dividing it into three sublists of almost n/3 items. This algorithm finds the sublist that might contain the given item and divides it into three smaller sublists of almost equal size. The algorithm repeats this process until it finds the item or concludes that the item is not in the list. Analyze your algorithm and give the results using order notation.	2015-11-08
7.	2015-11-08
8 ~ 9	2015-11-08
10. Write for the following problem a recursive algorithm whose worst-case time complexity is not worse than Θ(n ln n). Given a list of n distinct positive integers, partition the list into two sublists, each of size n/2, such that the difference between the sums of the integers in the two sublists is maximized. You may assume that n is a multiple of 2.		1. sort first 2. partition
11. Write a nonrecursive algorithm for Mergesort.	2015-11-08	If use iterator to implement the algorithm, pay attention to the mechanism implemented in the iterator to prevent out-of-index problem
12.
13. Write an algorithm that sorts a list of n items by dividing it into three sublists of about n/3 items, sorting each sublist recursively and merging the three sorted sublists.
14.	2015-11-08	46801
15 ~ 18	2015-11-08
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0
	2015-11-0

3 Dynamic Programming

4 The Greedy Approach

5 Backtracking

6 Branch-and-Bound

7 Introduction to Computational Complexity: The Sorting Problem

Any algorithm that sorts n distinct keys only by comparisons of keys and removes at most one inversion after each comparison must in the worst case do at least

and, on the average, do at least

章节学习纪录

Prologue

0.1 ~ 0.2	2015-11-22
0.3 a, b, c	2015-11-22	c = (log2( 1 + 5 ^ 0.5)) - 1

Algorithms with numbers

1.1 Show that in any base b 2, the sum of any three single-digit numbers is at most two digits long.	2015-11-22	3b - 3
1.2	2015-11-22	3.29
1.3 ~ 1.4	2015-11-22
1.5	2015-11-23
1.6	2015-11-23	multiplication is a kind of addition.
1.7	2015-11-23	O(n ^ 2)
1.8	2015-11-23	`def div(a, b): assert a >= 0 and b > 0 if a >= b: (q, r) = div(a >> 1, b) q = q << 1 r = r << 1 if (a & 1) == 1: r += 1 if r >= b: r-= b q += 1 else: q, r = 0, a return (q, r)`
1.9 ~ 1.10	2015-11-23
1.11	2015-11-23	divisible
1.12	2015-11-23	1
1.13	2015-11-23	yes
1.14 Suppose you want to compute the nth Fibonacci number Fn, modulo an integer p. Can you find an efficient way to do this?
1.15	2015-11-23	gcd(c, x) = 1
1.16 The algorithm for computing a^b mod c by repeated squaring does not necessarily lead to the minimum number of multiplications. Give an example of b > 10 where the exponentiation can be performed using fewer multiplications, by some other method.	2015-11-24	5 ^ 300 mod 124 = 1 because 5 ^ 3 mod 124 = 1, so repeated squaring does not lead to the minimum number of multiplications.
1.17
1.18, 1.19, 1.20, 1.21, 1.22, 1.23, 1.24, 1.25	2015-11-24	20 * 4 mod 79 = 1 3 * 21 mod 62 = 1 there is no inverse for 21 mod 91 5 * 14 mod 23 = 1 1330 - 121 of [2.. 1331] p^n - p^(n - 1) 2 ^ 126 mod 127 = 1 2 * 64 mod 127 = 1 so 2 ^ 125 mod 127 = 64
1.26 ~ 1.28	2015-11-25
1.29
1.30
1.31
1.32
1.33
1.34
1.35
1.36
1.37
1.38	2015-11-29	if (10^r) % p = 1, then ai x 10 ^ (i x r) % p = ai % p
1.39	2015-11-29	a ^ (p - 1) % p = 1, b ^ c % (p - 1) = ?
1.40	2015-11-29	N \| (x + 1)(x - 1), if N is prime, then N \| x + 1 or/and N \| x - 1.
1.41
1.42
1.43
1.44
1.45	2015-12-01
1.46	2015-12-01	a) if they use the same key pair for encrypt and sign. b) T ^ (e * d) % N = T <=> B * T ^ (e * d) % N = B * T
For any integer k > 0, an integer n is a *kth power* if there exists an integera such thata^k =n. Furthermore,n > 1 is a *nontrivial power* if it is akth power for some integerk > 1. Show how to determine whether a givenβ-bit integern is a nontrivial power in time polynomial in β.

Divide-and-conquer algorithms

Decompositions of graphs

3.1 ~ 3.2	2015-12-26
3.3	2015-12-26	8
3.4 ~ 3.6	2015-12-26
3.7 (b) Prove the following formulation: an undirected graph is bipartite if and only if it contains no cycles of odd length. (c) At most how many colors are needed to color in an undirected graph with exactly one odd length cycle?
3.8	2015-12-26	from __future__ import print_function import copy import random random.seed() class Container: def __init__(self, capacity, load = 0): self.capacity = capacity self.load = load def __eq__(self, other): return ( self.capacity == other.capacity and self.load == other.load ) def __ne__(self, other): return not self.__eq__(other) def __hash__(self): return hash(hash(self.capacity) * hash(self.load)) def __repr__(self): return "(%s\|%s)" % (self.capacity, self.load) class Containers: def __init__(self): self.containers = [] def __hash__(self): total = 0 for i in self.containers: total = total * 10 + hash(i) return hash(total) def __repr__(self): ret = "" for i in self.containers: if len(ret) > 0: ret += ", " ret += i.__repr__() return ret def __len__(self): return len(self.containers) def __eq__(self, other): equal = False n = len(self.containers) if n == len(other): equal = True for i in range(n): if self.containers[i] != other[i]: equal = False break return equal def __ne__(self, other): return not self.__eq__(other) def __getitem__(self, i): return self.containers[i] def add(self, c): self.containers.append(c) def select_target(state): random.seed() n = len(state) while True: t = random.randint(0, n - 1) if state[t].load < state[t].capacity: return t def select_source(state, target): random.seed() n = len(state) while True: s = random.randint(0, n - 1) if s != target and state[s].load > 0: return s #the difficulty is: how to get the next state, #the current implementation is too simple def next_state(state): n = len(state) new_state = copy.deepcopy(state) t = select_target(new_state) s = select_source(new_state, t) inc = min( new_state[t].capacity - new_state[t].load, new_state[s].load ) new_state[t].load += inc new_state[s].load -= inc return new_state def pouring_water(initial_state, end_condition): cache = set() path = [] current_state = initial_state while not end_condition(current_state): cache.add(current_state) path.append(current_state) while True: new_state = next_state(current_state) if new_state not in cache: current_state = new_state break path.append(current_state) for p in path: print(p) if __name__ == "__main__": initial_state = Containers() initial_state.add(Container(10, 0)) initial_state.add(Container(7, 7)) initial_state.add(Container(4, 4)) def stop(state): return state[1].load == 2 or state[2].load == 2 pouring_water(initial_state, stop)
3.9	2015-12-26	1. calculate the degree of every vertex; 2. for u in range(len(g)): for v in g.adj(u): total += degree[v]
3.10	2015-12-06
3.11	2015-12-27
3.12	2015-12-27	it is true
3.13	2015-12-27
3.14	2015-12-27	`def topological_sort_v2(g): ret = (True, []) n = len(g) if n > 0: exist = True seq = [] ind = [0 for i in range(n)] for i in range(n): for j in g.adj(i): ind[j.vertex] += 1 q = [] for i in range(n): if ind[i] == 0: q.append(i) for i in range(n): if q: j = q.pop(0) for k in g.adj(j): ind[k.vertex] -= 1 if ind[k.vertex] == 0: q.append(k.vertex) seq.append(j) else: exist = False break ret = (exist, seq) return ret`
3.15	2015-12-27	SCC cycle
3.16	2015-12-27	`def minimum_stages(g): n = len(g) ret = [] if n > 0: ind = [0 for i in range(n)] for i in range(n): for j in g.adj(i): ind[j.vertex] += 1 seq = [] for i in range(n): if ind[i] == 0: seq.append(i) while True: seq2 = [] for i in seq: for j in g.adj(i): ind[j.vertex] -= 1 if ind[j.vertex] == 0: seq2.append(j.vertex) ret.append(seq) if seq2: seq = seq2 else: break return ret`
3.17 (a) If p is an infinite trace, let Inf(p) V be the set of vertices that occur infinitely often in p. Show that Inf(p) is a subset of a strongly connected component of G.	2015-12-27
3.18	2015-12-27
3.19	2015-12-27	`def calculate_z_array(g, values): def dfs(g, values, s, accessed, ret): accessed[s] = True v = values[s] for u in g.adj(s): if not accessed[u]: v2 = dfs(g, values, u, accessed, ret) if v < v2: v = v2 ret[s] = v return v n = len(g) accessed = [False for i in range(n)] ret = [None for i in range(n)] for i in range(n): if not accessed[i]: dfs(g, values, i, accessed, ret) return ret`