Chapter 8 Exercises and Problems

Exercises
8.1-3 Show that there is no comparison sort whose running time is linear for at least half of the n! inputs of length n. What about a fraction of 1/n of the inputs of length n? What about a fraction 2^-n?
The answer is: no linear algorithm exists for any of the situations above. Here is the proof
Linear algorithm leads to at most c*n comparisons. According to the model of decision tree, only 2^(c*n) different states can be determined. If such a linear algorithm can run f(n) inputs of length n, 2^(c*n) = Ω(f(n))
a. f(n) = n! / 2, then 2^(c*n) = Ω(n!), which is obviously false
b. f(n) = (n-1)!, then 2^(c*n) = Ω((n-1)!), which is also false(you may use stirling formula to prove it)
c. f(n) = n! / 2^n, then 2^(c*n) = Ω(n! / 2^n)
<=> 2^((c+1)*n) = Ω(n!), which is also obviously false

8.2-2 Prove that COUNTING-SORT is stable
It is obvious because the items with the same key are placed in the destination array index-decreasingly. If we iterate these items in the original array also index-decreasingly, the sorting will be stable. COUNTING-SORT is just the case.

8.4-2 What is the worst-case running time for the bucket-sort algorithm? What simple change to the algorithm preserves its linear expected running time and makes its worst-case running time O(nlogn)?
The original worst-case running time is O(n^2). If we quicksort each bucket(you may optimize it by sorting by insertion sort if the bucket size is less than 20 or sth), you'll get a O(nlogn) worst-case running time without losing the expected running efficiency.

Problems
8-2 Sorting in place in linear time
e. Suppose that the n records have keys in the range from 1 to k. Show how to modify counting sort so that the records can be sorted in place in O(n+k) time. You may use O(k) storage outside the input array. Is your algorithm stable?
Despite the C array which is mentioned in counting sort, I'll introduce an additional D array. Say, C[0] = 0. Then C[i-1]+1 ~ C[i] is where the items with the key i lay. D array is defined, such that item D[i] indicates that D[i] ~ C[i] is currently UNsorted. Then, the initial value of D[i] is C[i-1]+1 (O(k) process time).
The complete algorithm is shown below: (I've omitted the construction of C array and initialization of D array)
for (j = 1 ;j <= n;j ++ )
... {
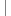    KEY_TYPE key = A[j].key;
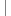    swap(A[j],A[D[key]]);
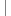    D[key]++;
}
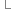Therefore, the algorithm can run in O(n+k) with O(k) outside storage to sort the records.
The sorting is not stable, since the A[j] <-> A[D[key]] swapping may reverse the relative order of items with key A[D[key]].key

Well, here I'll raise a question from question a~c: Suppose k=2 in the situation above, can you design an algorithm, which runs in O(n) time, is stable, and sorts in place(O(1) additional storage, including output array)?
It is easy to design algorithms to satisfy any two of the three requirements. But it's quite difficult to meet all of them. It even remains a question whether there is one. But I cannot prove that it does not exist. If anyone solves this problem, welcome to leave your message here to share your points~.~

8-3 Sorting variable-length items
a. You're given an array of integers, where different integers may have different numbers of digits, but the total number of digits over all the integers in the array is n. Show how to sort the array in O(n) time.
First, bucket the array in O(n) time to classify these integers by their number of digits.
Then, for each bucket, use radix sort to sort them in O(k*b[k]), where k is the digit of one integer, and b[k] is the number of integers that have k digits.
Since sigma(k=1~+inf,k*b[k]) = n, all the radix sorts make a O(n) complexity. Therefore, the algorithm is O(n).

b. What if you're given an array of strings and you're to sort in alphabetical order?
Establish a prefix tree for the strings. Pre-orderly traverse the tree to finish the sorting. Since there are n characters in all, the nodes in the tree are at most n. Thus the running time is O(n). A similar problem is raised in Problem 12-2.

转载于:https://www.cnblogs.com/FancyMouse/articles/1052062.html