一 图算法合集
1 广度优先遍历 - BFS
#include<iostream>
#include<queue>
#include<stack>
#include<stdlib.h>
#define MAX 100
using namespace std;
typedef struct
{
int edges[MAX][MAX]; //邻接矩阵
int n; //顶点数
int e; //边数
}MGraph;
bool visited[MAX]; //标记顶点是否被访问过
void creatMGraph(MGraph &G) //用引用作参数
{
int i,j;
int s,t; //存储顶点编号
int v; //存储边的权值
for(i=0;i<G.n;i++) //初始化
{
for(j=0;j<G.n;j++)
{
G.edges[i][j]=0;
}
visited[i]=false;
}
for(i=0;i<G.e;i++) //对矩阵相邻的边赋权值
{
scanf("%d %d %d",&s,&t,&v);
//两个顶点确定一条边
//输入边的顶点编号以及权值
G.edges[s][t]=v;
}
}
void DFS(MGraph G,int v) //深度优先搜索
{
int i;
printf("%d ",v); //访问结点v
visited[v]=true;
for(i=0;i<G.n;i++) //访问与v相邻的未被访问过的结点
{
if(G.edges[v][i]!=0&&visited[i]==false)
{
DFS(G,i);//若没访问则继续，而且根据顶点的序号按数序访问
}
}
}
//stack弹出顺序有问题
void DFS1(MGraph G,int v) //非递归实现
{
stack<int> s;
printf("%d ",v); //访问初始结点
visited[v]=true;
s.push(v); //入栈
while(!s.empty())
{
int i,j;
i=s.top(); //取栈顶顶点
for(j=0;j<G.n;j++) //访问与顶点i相邻的顶点
{
if(G.edges[i][j]!=0&&visited[j]==false)
{
printf("%d ",j); //访问
visited[j]=true;
s.push(j); //访问完后入栈
break; //找到一个相邻未访问的顶点，访问之后则跳出循环
}
}
//对于节点4，找完所有节点发现都已访问过或者没有临边，所以j此时=节点总数，然后把这个4给弹出来
直到弹出1，之前的深度搜索的值都已弹出，有半部分还没有遍历，开始遍历有半部分
if(j==G.n) //如果与i相邻的顶点都被访问过，则将顶点i出栈
s.pop();
}
}
void BFS(MGraph G,int v) //广度优先搜索
{
queue<int> Q; //STL模板中的queue
printf("%d ",v);
visited[v]=true;
Q.push(v);
while(!Q.empty())
{
int i,j;
i=Q.front(); //取队首顶点
Q.pop();//弹出一个，然后遍历这个节点的子节点，然后遍历完再弹出下一个
for(j=0;j<G.n;j++) //广度遍历
{
if(G.edges[i][j]!=0&&visited[j]==false)
{
printf("%d ",j);
visited[j]=true;
Q.push(j);
}
}
}
}
int main(void)
{
int n,e; //建立的图的顶点数和边数
while(scanf("%d %d",&n,&e)==2&&n>0)
{
MGraph G;
G.n=n;
G.e=e;
creatMGraph(G);
DFS(G,0);
printf("\n");
// DFS1(G,0);
// printf("\n");
// BFS(G,0);
// printf("\n");
}
return 0;
}
2 强连通分量 - SCC
三种主要的算法: 算法Kosaraju,Trajan,Gabow
Kosaraju算法
Kosaraju算法复杂度O(N)。一个有向图的强连通分量，能够收缩为一个点，统计最后点的个数，即是强连通分量的个数。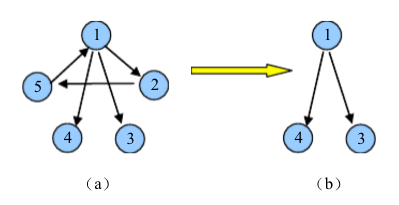
Kosaraju算法的思想讲解：
1） 对原图进行深搜（DFS），得到一个深搜出栈的顺序。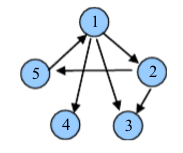
假设出栈顺序 3→5→2→4→1
2） 将原图每条边进行反向。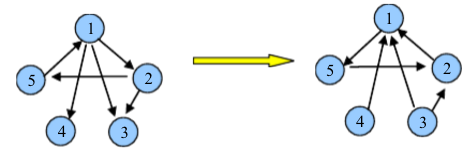
3） 按第一步生成的出栈顺序的逆序，对反图进行搜索 
并且在每轮搜索中对搜到的点进行染色。
显然，每条边都进行反向后，在反图中按出栈的逆序也能搜到的连通块一定是强连通块。 因为如果是强连通子图，那么反向没有任何影响，依然是强连通子图。但如果是单向的边连通，反向后再按原序就无法访问了（因此反向处理是对非强 连通块的过滤）。
Tarjan 算法
下图（图片来自这里）中 顶点 {1,2,3,4}是一个强连通分量，因为它们两两都可以到达。直观上来讲，所谓的强连通，（如果有至少有一个顶点）就是可以至少形成一个环。如1->3->4->1就是一个环，它们就是强连通的。注意也有像{5},{6}这样的的连通分量。
强连通的tarjan 算法是基于图的深度优先搜索（这个经常用于获取图的各种信息）。下面说一下几个约定：
时间戳 ：DFN[i]是指结点i被遍历的时间。 Low[i] ：是指在搜索树中，结点i和其子孙可以访问到的最早的祖先，Low[i] = Min(DFN[i], DFN[j], Low[k])其中j是i的祖先（我们把子孙连到祖先的边叫后向边），k是i 的子女。 结点的颜色：color[i]是用于标示结点i的状态：白色指还没到搜索到，灰色正在被搜索，黑色处理完毕。在实际操作中用-1,0,1分别代表白色、灰色、黑色。
tarjan算法的步骤：
- 这里是列表文本先把所有的结点的颜色都初始化白色，并把栈清空。
- 找到一个白色的结点i（即结点的颜色为白色）给结点一个时间戳，把结点圧入栈中，并把结点标记为灰色。令Low[i] = DFN[i]
- 遍历结点i 的每条边(i,j)。若color[j]是白色，就对结点i重复2～5步骤。并令Low[i] = min(Low[j],low[i]).如果color[j]是灰色，令Low[i] = min(Low[i],DFN[j])。如果是黑色不做任何处理。
- 把结点的颜色改为黑色，如果Low[i] = DFN[i]，就把从栈顶到结点i间的元素弹出
- 重复步骤2，至到没有白色顶点
#include <stdio.h>
#include <string.h>
#include <vector>
#define MIN(a,b) ((a)<(b)?(a):(b))
using namespace std;
#define N 100
int pre[N],low[N],id[N],s[N],t,cnt,top,n,m;
vector<int> g[N];
//初始化
void init()
{
t=cnt=top=0;
memset(pre,0xff,sizeof(pre));
}
//tarjan算法主体
void dfs(int u)
{
int min=pre[u]=low[u]=t++;
int i,v;
s[top++]=u;
for(i=0;i<g[u].size();i++)
{
v=g[u][i];
if(pre[v]==-1) dfs(v);
min=MIN(min,low[v]);
}
if(min<low[u])
{
low[u]=min;
return;
}
do{
id[v=s[--top]]=cnt;
low[v]=n;
}while(v!=u);
cnt++;
}
//调用测试
int main()
{
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
int u,v,i,kase=0;
while(~scanf("%d%d",&n,&m))
{
for(i=0;i<n;i++) g[i].clear();
for(i=0;i<m;i++)
{
scanf("%d%d",&u,&v);
g[u].push_back(v);
}
init();
for(i=0;i<n;i++)
{
if(pre[i]==-1) dfs(i);
}
for(i=0;i<cnt;i++) g[i].clear();
for(i=0;i<n;i++)
{
g[id[i]].push_back(i);
}
printf("Case %d: ",++kase);
for(i=0;i<cnt;i++)
{
printf("{ ");
for(int j=0;j<g[i].size();j++)
{
printf("%d ",g[i][j]);
}
printf("} ");
}
printf("\n");
}
return 0;
}
3 Weakly Connected Components
4 TriangleCount
You will need depth first search. The algorithm will be:
- For the current node ask all unvisited adjacent nodes
- for each of those nodes run depth two check to see if a node at depth 2 is your current node from step one
- mark current node as visited
- on make each unvisited adjacent node your current node (1 by 1) and run the same algorithm
5 Connected Components
Hash-Min algorithm
6 Boruvka’s minimum spanning tree algorithm
Prim算法和Kruskal算法
7 PageRank
8 HITS
HITS算法与PageRank算法比较 HITS算法和PageRank算法可以说是搜索引擎链接分析的两个最基础且最重要的算法。从以上对两个算法的介绍可以看出，两者无论是在基本概念模型还是计算思路以及技术实现细节都有很大的不同，下面对两者之间的差异进行逐一说明。
1.HITS算法是与用户输入的查询请求密切相关的，而PageRank与查询请求无关。所以，HITS算法可以单独作为相似性计算评价标准，而PageRank必须结合内容相似性计算才可以用来对网页相关性进行评价；
2.HITS算法因为与用户查询密切相关，所以必须在接收到用户查询后实时进行计算，计算效率较低；而PageRank则可以在爬虫抓取完成后离线计算，在线直接使用计算结果，计算效率较高；
3.HITS算法的计算对象数量较少，只需计算扩展集合内网页之间的链接关系；而PageRank是全局性算法，对所有互联网页面节点进行处理；
4.从两者的计算效率和处理对象集合大小来比较，PageRank更适合部署在服务器端，而HITS算法更适合部署在客户端；
5.HITS算法存在主题泛化问题，所以更适合处理具体化的用户查询；而PageRank在处理宽泛的用户查询时更有优势；
6.HITS算法在计算时，对于每个页面需要计算两个分值，而PageRank只需计算一个分值即可；在搜索引擎领域，更重视HITS算法计算出的Authority权值，但是在很多应用HITS算法的其它领域，Hub分值也有很重要的作用；
7.从链接反作弊的角度来说，PageRank从机制上优于HITS算法，而HITS算法更易遭受链接作弊的影响。
8.HITS算法结构不稳定，当对“扩充网页集合”内链接关系作出很小改变，则对最终排名有很大影响；而PageRank相对HITS而言表现稳定，其根本原因在于PageRank计算时的“远程跳转”。
9 单源最短路经 - SSSP
10 Semi-clustering
11 Random Bipartite Matching [28]
12 Approx. Maximum Weight Matching [41]
二分图的最大匹配、完美匹配和匈牙利算法 August 1, 2013 / 算法 这篇文章讲无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。
二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 UU 和VV ，使得每一条边都分别连接UU、VV中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。
匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。
Bipartite Graph(1) Bipartite Graph(2) Matching Maximum Matching
我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。
完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。
举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。
0
基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。
5
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：
增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。
匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：
7 8 9
这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。
下面给出匈牙利算法的 DFS 和 BFS 版本的代码：
// 顶点、边的编号均从 0 开始
// 邻接表储存
struct Edge
{
int from;
int to;
int weight;
Edge(int f, int t, int w):from(f), to(t), weight(w) {}
};
vector<int> G[__maxNodes]; /* G[i] 存储顶点 i 出发的边的编号 */
vector<Edge> edges;
typedef vector<int>::iterator iterator_t;
int num_nodes;
int num_left;
int num_right;
int num_edges;
int matching[__maxNodes]; /* 存储求解结果 */
int check[__maxNodes];
bool dfs(int u)
{
for (iterator_t i = G[u].begin(); i != G[u].end(); ++i) { // 对 u 的每个邻接点
int v = edges[*i].to;
if (!check[v]) { // 要求不在交替路中
check[v] = true; // 放入交替路
if (matching[v] == -1 || dfs(matching[v])) {
// 如果是未盖点，说明交替路为增广路，则交换路径，并返回成功
matching[v] = u;
matching[u] = v;
return true;
}
}
}
return false; // 不存在增广路，返回失败
}
int hungarian()
{
int ans = 0;
memset(matching, -1, sizeof(matching));
for (int u=0; u < num_left; ++u) {
if (matching[u] == -1) {
memset(check, 0, sizeof(check));
if (dfs(u))
++ans;
}
}
return ans;
}
queue<int> Q;
int prev[__maxNodes];
int Hungarian()
{
int ans = 0;
memset(matching, -1, sizeof(matching));
memset(check, -1, sizeof(check));
for (int i=0; i<num_left; ++i) {
if (matching[i] == -1) {
while (!Q.empty()) Q.pop();
Q.push(i);
prev[i] = -1; // 设 i 为路径起点
bool flag = false; // 尚未找到增广路
while (!Q.empty() && !flag) {
int u = Q.front();
for (iterator_t ix = G[u].begin(); ix != G[u].end() && !flag; ++ix) {
int v = edges[*ix].to;
if (check[v] != i) {
check[v] = i;
Q.push(matching[v]);
if (matching[v] >= 0) { // 此点为匹配点
prev[matching[v]] = u;
} else { // 找到未匹配点，交替路变为增广路
flag = true;
int d=u, e=v;
while (d != -1) {
int t = matching[d];
matching[d] = e;
matching[e] = d;
d = prev[d];
e = t;
}
}
}
}
Q.pop();
}
if (matching[i] != -1) ++ans;
}
}
return ans;
}
匈牙利算法的要点如下
从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。
如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数 +1，停止搜索。 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈，而 BFS 版本使用 prev 数组。
性能比较
两个版本的时间复杂度均为O(V⋅E)O(V⋅E)。DFS 的优点是思路清晰、代码量少，但是性能不如 BFS。我测试了两种算法的性能。对于稀疏图，BFS 版本明显快于 DFS 版本；而对于稠密图两者则不相上下。在完全随机数据 9000 个顶点 4,0000 条边时前者领先后者大约 97.6%，9000 个顶点 100,0000 条边时前者领先后者 8.6%, 而达到 500,0000 条边时 BFS 仅领先 0.85%。
补充定义和定理：
最大匹配数：最大匹配的匹配边的数目
最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择
最大独立数：选取最多的点，使任意所选两点均不相连
最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。
定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）
定理2：最大匹配数 = 最大独立数
定理3：最小路径覆盖数 = 顶点数 - 最大匹配数
13 Diameter Estimation (Double Fringe) [38]
14 Minimum Spanning Forest [41]
15 Graph Coloring [41]
Graph Coloring | Set 2 (Greedy Algorithm)
We introduced graph coloring and applications in previous post. As discussed in the previous post, graph coloring is widely used. Unfortunately, there is no efficient algorithm available for coloring a graph with minimum number of colors as the problem is a known NP Complete problem. There are approximate algorithms to solve the problem though. Following is the basic Greedy Algorithm to assign colors. It doesn’t guarantee to use minimum colors, but it guarantees an upper bound on the number of colors. The basic algorithm never uses more than d+1 colors where d is the maximum degree of a vertex in the given graph.
Basic Greedy Coloring Algorithm:
- Color first vertex with first color.
- Do following for remaining V-1 vertices. a) Consider the currently picked vertex and color it with the lowest numbered color that has not been used on any previously colored vertices adjacent to it. If all previously used colors appear on vertices adjacent to v, assign a new color to it. Following are C++ and Java implementations of the above Greedy Algorithm.
C++
// A C++ program to implement greedy algorithm for graph coloring
#include <iostream>
#include <list>
using namespace std;
// A class that represents an undirected graph
class Graph
{
int V; // No. of vertices
list<int> *adj; // A dynamic array of adjacency lists
public:
// Constructor and destructor
Graph(int V) { this->V = V; adj = new list<int>[V]; }
~Graph() { delete [] adj; }
// function to add an edge to graph
void addEdge(int v, int w);
// Prints greedy coloring of the vertices
void greedyColoring();
};
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v); // Note: the graph is undirected
}
// Assigns colors (starting from 0) to all vertices and prints
// the assignment of colors
void Graph::greedyColoring()
{
int result[V];
// Assign the first color to first vertex
result[0] = 0;
// Initialize remaining V-1 vertices as unassigned
for (int u = 1; u < V; u++)
result[u] = -1; // no color is assigned to u
// A temporary array to store the available colors. True
// value of available[cr] would mean that the color cr is
// assigned to one of its adjacent vertices
bool available[V];
for (int cr = 0; cr < V; cr++)
available[cr] = false;
// Assign colors to remaining V-1 vertices
for (int u = 1; u < V; u++)
{
// Process all adjacent vertices and flag their colors
// as unavailable
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (result[*i] != -1)
available[result[*i]] = true;
// Find the first available color
int cr;
for (cr = 0; cr < V; cr++)
if (available[cr] == false)
break;
result[u] = cr; // Assign the found color
// Reset the values back to false for the next iteration
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (result[*i] != -1)
available[result[*i]] = false;
}
// print the result
for (int u = 0; u < V; u++)
cout << "Vertex " << u << " ---> Color "
<< result[u] << endl;
}
// Driver program to test above function
int main()
{
Graph g1(5);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(1, 3);
g1.addEdge(2, 3);
g1.addEdge(3, 4);
cout << "Coloring of graph 1 \n";
g1.greedyColoring();
Graph g2(5);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(1, 2);
g2.addEdge(1, 4);
g2.addEdge(2, 4);
g2.addEdge(4, 3);
cout << "\nColoring of graph 2 \n";
g2.greedyColoring();
return 0;
}
Run on IDE
Output: Coloring of graph 1 Vertex 0 ---> Color 0 Vertex 1 ---> Color 1 Vertex 2 ---> Color 2 Vertex 3 ---> Color 0 Vertex 4 ---> Color 1
Coloring of graph 2 Vertex 0 ---> Color 0 Vertex 1 ---> Color 1 Vertex 2 ---> Color 2 Vertex 3 ---> Color 0 Vertex 4 ---> Color 3 Time Complexity: O(V^2 + E) in worst case.
Analysis of Basic Algorithm The above algorithm doesn’t always use minimum number of colors. Also, the number of colors used sometime depend on the order in which vertices are processed. For example, consider the following two graphs. Note that in graph on right side, vertices 3 and 4 are swapped. If we consider the vertices 0, 1, 2, 3, 4 in left graph, we can color the graph using 3 colors. But if we consider the vertices 0, 1, 2, 3, 4 in right graph, we need 4 colors.
So the order in which the vertices are picked is important. Many people have suggested different ways to find an ordering that work better than the basic algorithm on average. The most common is Welsh–Powell Algorithm which considers vertices in descending order of degrees.
How does the basic algorithm guarantee an upper bound of d+1? Here d is the maximum degree in the given graph. Since d is maximum degree, a vertex cannot be attached to more than d vertices. When we color a vertex, at most d colors could have already been used by its adjacent. To color this vertex, we need to pick the smallest numbered color that is not used by the adjacent vertices. If colors are numbered like 1, 2, …., then the value of such smallest number must be between 1 to d+1 (Note that d numbers are already picked by adjacent vertices). This can also be proved using induction. See this video lecture for proof.
We will soon be discussing some interesting facts about chromatic number and graph coloring.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
图的m色判定问题--贪心算法
给定无向连通图G和m种颜色。用这些颜色为图G的各顶点着色.问是否存在着色方法,使得G中任2邻接点有不同颜色。 图的m色优化问题:给定无向连通图G,为图G的各顶点着色, 使图中任2邻接点着不同颜色,问最少需要几种颜色。所需的最少颜色的数目m称为该图的色数。若图G是可平面图,则它的色数不超过4色(4色定理).4色定理的应用:在一个平面或球面上的任何地图能够只用4种颜色来着色使得相邻的国家在地图上着有不同颜色,任意图的着色 Welch Powell法 a).将G的结点按照度数递减的次序排列. b).用第一种颜色对第一个结点着色,并按照结点排列的次序 对与前面着色点不邻接的每一点着以相同颜色. c).用第二种颜色对尚未着色的点重复步骤b).用第三种颜色
继续这种作法, 直到所有点着色完为止.
[cpp] view plaincopy
#include <fstream>
#include <iostream>
#include <stdlib.h>
#include <algorithm>
using namespacestd;
int map[10][10];//邻接矩阵
typedef structNode{ //定义节点结构体
int index; //编号
int degree; //度
int color; //改节点的颜色
} Node;
Nodenodes[10];
bool com(Nodenode1,Nodenode2) { //按度从高到低排序
return node1.degree > node2.degree;
}
bool com2(Nodenode1,Nodenode2) { //按度从高到低排序
return node1.index < node2.index;
}
int main() {
ifstream read;
read.open("map.data");//map.data是存放数据的文件名
int m, n;
while (read >> m>> n) {
for (int i = 0; i < m; i++) {//读入数据
int degree = 0;
for (int j = 0; j < n; j++) {
read>> map[i][j];
if (map[i][j])
degree++;
}
nodes[i].index = i;
nodes[i].degree = degree;
nodes[i].color = 0;
}
//排序
sort(nodes,nodes + m, com);
int k = 0;//K 代表第几种颜色
while (true) {
k++;
int i;
for (i = 0; i < m; i++){//先找到第一个未着色的节点
if (nodes[i].color == 0) {
nodes[i].color = k;
break;
}
}
if (i == m)//循环退出的条件,所有节点都已着色
break;
//再把所有不和该节点相邻的节点着相同的颜色
for(int j=0; j<m; j++){
if(nodes[j].color ==0 &&map[nodes[i].index][nodes[j].index] == 0
&&i!=j)
nodes[j].color = k;
}
}
//输出结果：
sort(nodes,nodes + m, com2);
cout << "共需要" << k-1 << "种颜色" << endl;
for (int i = 0; i < m; i++)
cout<< "节点："<<nodes[i].index <<":着色" << nodes[i].color <<endl;
return 0;
}
}
测试数据(map.data):
8 8
0 1 1 1 0 0 1 0
1 0 1 1 1 0 0 0
1 1 0 0 1 1 0 0
1 1 0 0 1 0 1 0
0 1 1 1 0 1 1 1
0 0 1 0 1 0 0 1
1 0 1 1 1 0 0 1
0 0 0 0 1 1 10
即： 运行结果; 共需要3种颜色 节点：1:着色1 节点：2:着色2 节点：3:着色3 节点：4:着色3 节点：5:着色1 节点：6:着色2 节点：7:着色2 节点：8:着色3
16 Maximal Independent Set [41]
17 K-core [38]
18 Clustering Coefficient [38]
19 K-truss [38]
20 Simple METIS [29]
21 Multilevel clustering [33]
22 Graph Partition
Metis
Voronoi digraph
skeleton digraph
gradient based
Max Flow and minimum cut
定理：可行流 f﹡是最大流，当且仅当不存在关于 f﹡的增广链。
证明：必要性：设 f﹡是最大流，若存在关于 f﹡的增广链μ，令
则θ ＞0，令
示例代码:
import java.util.LinkedList;
import java.util.Queue;
public class MinFlow {
public static int V = 6;
/**
*
* @param rGraph 残留网络
* @param s 源点
* @param t 终点
* @param path 路径
* @return 是否可以在rGraph中找到一条从 s 到 t 的路径
*/
public static boolean hasPath(int rGraph[][], int s, int t, int path[]) {
boolean visited[] = new boolean[V];
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
//标准的BFS算法
while(queue.size() > 0){
int top = queue.poll();
for(int i=0; i<V; i++){
if(!visited[i] && rGraph[top][i] > 0){
queue.add(i);
visited[i] = true;
path[i] = top;
}
}
}
return visited[t] == true;
}
/**
*
* @param graph 有向图的矩阵表示
* @param s 源点
* @param t 终点
* @return 最大流量
*/
private static int maxFlow(int[][] graph,int s, int t) {
int rGraph[][] = new int[V][V];
for(int i=0; i<V; i++)
for(int j=0; j<V; j++)
rGraph[i][j] = graph[i][j];
int maxFlow = 0;
int path[] = new int[V];
while(hasPath(rGraph, s, t, path)){
int min_flow = Integer.MAX_VALUE;
//更新路径中的每条边,找到最小的流量
for(int v=t; v != s; v=path[v]){
int u = path[v];
min_flow = Math.min(min_flow, rGraph[u][v]);
}
//更新路径中的每条边
for(int v=t; v != s; v=path[v]){
int u = path[v];
rGraph[u][v] -= min_flow;
rGraph[v][u] += min_flow;
}
maxFlow += min_flow;
}
return maxFlow;
}
public static void main(String[] args) {
//创建例子中的有向图
int graph[][] = { { 0, 16, 13, 0, 0, 0 },
{ 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 },
{ 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 },
{ 0, 0, 0, 0, 0, 0 } };
V = graph.length;
int flow = maxFlow(graph, 0, 5);
System.out.println("The maximum possible flow is :" + flow);
}
}
- Motivation:
分布并不均匀 - 定义顶点间的梯度, 概率密度函数
二 矩阵计算的并行化
I. 胡峰, & 胡保生. (1999). 并行计算技术与并行算法综述. 电脑与信息技术(5), 47-59.
II. Heller ( 1978) 《数值线性代数的并行算法综述》
1 矩阵乘法
2 矩阵的三角形LU分解的向量迭代算法
其处理思想和分解算法对于矩阵求逆线性方程组求解、乃至整个矩阵运算的并行化处理都有参考和使用价值
3 求解矩阵特征值
Householder方法和QR算法也是较常用的。 ward(1976)考虑了在向量计算机上实现QR算法和Hyman方法的并行处理技术。
线性方 程组的 Gauss 消元法
Jaeobi 迭代法
线性回归的 Housheolder 求解算法
线性系统的并行算法
递归问题的并行处理
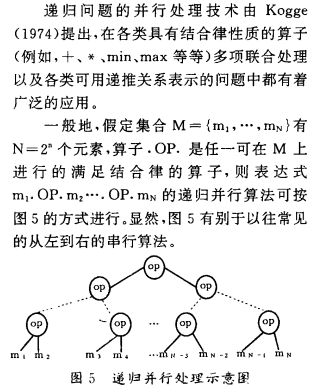
三 图象并行处理技术
四 分类与排序问题的并行处理
五 并行搜索与组合搜索的并行化处理
reference
[28] G.Malewicz,M.H.Austern,A.J.C.Bik,J.C.Dehnert,I.Horn, N. Leiser, and G. Czajkowski. Pregel: A System for Large-Scale Graph Processing. In Proceedings of the ACM SIGMOD International Conference on Management of Data, 2011.
[29] METISGraphPartitionLibrary.http://exoplanet.eu/catalog.php.
[33] S.OliveiraandS.C.Seok.MultilevelApproachesforLarge-scale Proteomic Networks. International Journal of Computer Mathematics, 84(5), 2007.
[38] L.Quick,P.Wilkinson,andD.Hardcastle.UsingPregel-likeLarge Scale Graph Processing Frameworks for Social Network Analysis. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining, 2012.
[41] S.SalihogluandJ.Widom.OptimizingGraphAlgorithmson Pregel-like Systems. In Proceedings of the International Conference on Very Large Databases, 2014.
306
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
