一、并查集 (Union-Find Set）

如果：给出各个元素之间的联系，要求将这些元素分成几个集合，每个集合中的元素直接或间接有联系。在这类问题中主要涉及的是对集合的合并和查找，因此将这种集合称为并查集。 
链表被普通用来计算并查集.表中的每个元素设两个指针：一个指向同一集合中的下一个元素；另一个指向表首元素。 

链结构的并查集 

采用链式存储结构，在进行集合查找时的算法复杂度仅为O（1）；但合并集合时的算法复杂度却达到了O（n）。如果我们希望两种基本操作的时间效率都比较高的话，链式存储方式就“力不从心”了。 

树结构的并查集 

采用树结构支持并查集的计算能够满足我们的要求。并查集与一般的树结构不同，每个顶点纪录的不是它的子结点，而是将它的父结点记录下来。下面是树结构的并查集的两种运算方式 

⑴直接在树中查询 
⑵边查询边“路径压缩” 

对应与前面的链式存储结构，树状结构的优势非常明显：编程复杂度低；时间效率高。 

直接在树中查询 

集合的合并算法很简单，只要将两棵树的根结点相连即可，这步操作只要O（1）时间复杂度。算法的时间效率取决于集合查找的快慢。而集合的查找效率与树的深度呈线性关系。因此直接查询所需要的时间复杂度平均为O（logN）。但在最坏情况下，树退化成为一条链，使得每一次查询的算法复杂度为O（N）。 

边查询边“路径压缩 

其实，我们还能将集合查找的算法复杂度进一步降低：采用“路径压缩”算法。它的想法很简单：在集合的查找过程中顺便将树的深度降低。采用路径压缩后，每一次查询所用的时间复杂度为增长极为缓慢的ackerman函数的反函数——α（x）。对于可以想象到的n，α（n）都是在5之内的。

并查集：(union-find sets)是一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多。一般采取树形结构来存储并查集，并利用一个rank数组来存储集合的深度下界，在查找操作时进行路径压缩使后续的查找操作加速。这样优化实现的并查集，空间复杂度为O(N)，建立一个集合的时间复杂度为O(1)，N次合并M查找的时间复杂度为O(M Alpha(N))，这里Alpha是Ackerman函数的某个反函数，在很大的范围内（人类目前观测到的宇宙范围估算有10的80次方个原子，这小于前面所说的范围）这个函数的值可以看成是不大于4的，所以并查集的操作可以看作是线性的。它支持以下三中种操作:

　　－Union (Root1, Root2) //并操作；把子集合Root2并入集合Root1中.要求：Root1和 Root2互不相交,否则不执行操作.

　　－Find (x) //搜索操作；搜索单元素x所在的集合,并返回该集合的名字.

　　－UFSets (s) //构造函数。将并查集中s个元素初始化为s个只有一个单元素的子集合.

　　－对于并查集来说，每个集合用一棵树表示。

　　－集合中每个元素的元素名分别存放在树的结点中，此外，树的每一个结点还有一个指向其双亲结点的指针。

　　－设 S1= {0, 6, 7, 8 }，S2= { 1, 4, 9 }，S3= { 2, 3, 5 }

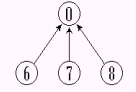
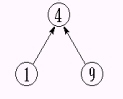
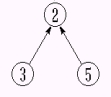
－为简化讨论，忽略实际的集合名，仅用表示集合的树的根来标识集合。

　　－为此，采用树的双亲表示作为集合存储表示。集合元素的编号从0到 n-1。其中 n 是最大元素个数。在双亲表示中，第 i 个数组元素代表包含集合元素 i 的树结点。根结点的双亲为-1，表示集合中的元素个数。为了区别双亲指针信息( ≥ 0 )，集合元素个数信息用负数表示。　　　

下标  parent

集合S1, S2和S3的双亲表示: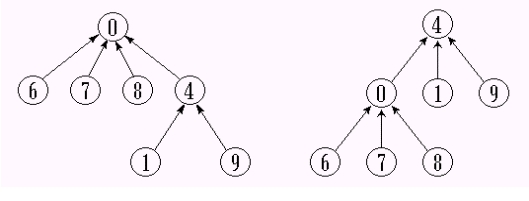

                  　　　        S1 ∪ S2的可能的表示方法

const int DefaultSize = 10;

　　class UFSets { //并查集的类定义

　　private:

　　　int *parent;

　　　int size;

　　public:

　　　UFSets ( int s = DefaultSize );

　　　~UFSets ( ) { delete [ ] parent; }

　　　UFSets & operator = ( UFSets const & Value );//集合赋值

　　　void Union ( int Root1, int Root2 );

　　　int Find ( int x );

　　　void UnionByHeight ( int Root1, int Root2 ); };

　　　UFSets::UFSets ( int s ) { //构造函数

　　　size = s;

　　　parent = new int [size+1];

　　　for ( int i = 0; i <= size; i++ ) parent[i] = -1;

　　}

　　unsigned int UFSets::Find ( int x ) { //搜索操作

　　　if ( parent[x] <= 0 ) return x;

　　　else return Find ( parent[x] );

　　}

　　void UFSets::Union ( int Root1, int Root2 ) { //并

　　　parent[Root2] = Root1; //Root2指向Root1

　　}

Find和Union操作性能不好。假设最初 n 个元素构成 n 棵树组成的森林，parent[i] = -1。做处理Union(0, 1), Union(1, 2), …, Union(n-2, n-1)后，将产生如图所示的退化的树。

                             

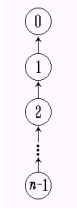
执行一次Union操作所需时间是O(1)，n-1次Union操作所需时间是O(n)。若再执行Find(0), Find(1), …, Find(n-1), 若被

搜索的元素为i，完成Find(i)操作需要时间为O(i)，完成 n 次搜索需要的总时间将达到

　            　

Union操作的加权规则

　　为避免产生退化的树，改进方法是先判断两集合中元素的个数，如果以 i 为根的树中的结点个数少于以 j 为根的树中的结点个数，即parent[i] > parent[j]，则让 j 成为 i 的双亲，否则，让i成为j的双亲。此即Union的加权规则。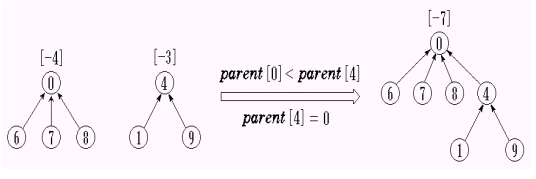

              parent[0](== -4) < parent[4] (== -3)

 

　　void UFSets::WeightedUnion(int Root1, int Root2) {

　　　//按Union的加权规则改进的算法

　　　int temp = parent[Root1] + parent[Root2];

　　　if ( parent[Root2] < parent[Root1] ) {

　　　　parent[Root1] = Root2; //Root2中结点数多

　　　　parent[Root2] = temp; 　//Root1指向Root2

　　　}

　　　else {

　　　　parent[Root2] = Root1; //Root1中结点数多

　　　　parent[Root1] = temp; 　//Root2指向Root1

　　　}

　　}

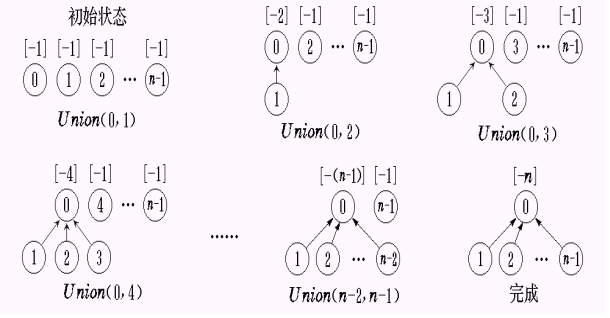
                           　使用加权规则得到的树

 

 评论这张