并查集(Union-Find)算法详解

并查集（Union-Find）是解决动态连通性问题的一类非常高效的数据结构。本文中，我将尽我所能用最简单，最清晰的逻辑展示出并查集的构造过程，同时还将对其中的关键步骤给出相应的Python代码。

动态连通性

可以想象一张地图上有很多点，有些点之间是有道路相互联通的，而有些点则没有。如果我们现在要从点A走向点B，那么一个关键的问题就是判断我们能否从A走到B呢？换句话说，A和B是否是连通的。这是动态连通性最基本的诉求。现在给出一组数据，其中每个元素都是一对“点”，代表这对点之间是联通的，我们需要设计一个算法，让计算机依次读取这些数据，最后判断出其中任意两点是否连通。注意，并查集所涉及的动态连通性只是考虑“是否连通”这一二值判别问题，而不涉及连通的路径到底是什么。后者不在本文的考虑范围之内。

举个例子，比如下图。为了简单起见，我们以整数 0~9 表示图中的10个点，然后给出两两连通的数据如下：[(4, 3), (3, 8), (6, 5), (9, 4), (2, 1), (8, 9), (5, 0), (7, 2), (6, 1), (6, 7)]

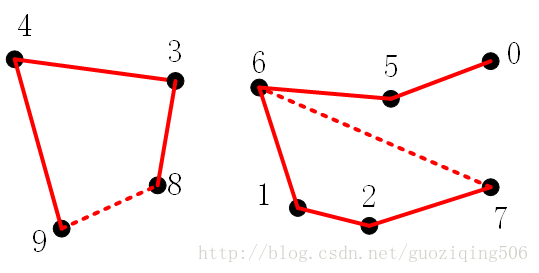
我们将这些“点对”依次通过画图连接的方式在图中表示出来。当然，如果其中某“对”点本身就是连通的，比如点对$(8, 9)$，还有$(6, 7)$在连接前就已经是连通的，我们可以自动忽略这种情况。通过这张图，可以直观的看出，有些点对，像0与1是相互连通的，而有些像0与9是不连通的。现在的问题是，如何让计算机读取这些数据来构建一种数据结构（合并连通点），然后在这种数据结构上高效的做出对某个点对是否连通的判断（查询连通性）。这也就是并查集名字的由来了。

为了实现上面所描述的功能，一个简单的思路就是分组。也就是说，我们可以把相互连通的点看成一个组，如果现在查询的点对分别在不同的组中，则这个点对不连通，否则连通。下面我们先来简单分析一下这种操作的具体过程，分“并”和“查”两个方面来分析。为了方便描述，我这里先举一个例子：比如上图的10个点，现在就令每个点的值为其初始组别，我们可以得到下面这个表：

element	0	1	2	3	4	5	6	7	8	9
group number	0	1	2	3	4	5	6	7	8	9

现在，“并”的操作可以这样来描述：观察第一个点对$(4, 3)$，于是先找到点4和3，发现所在组别不一样，再将点4和3的组别都变成3（当然都变成4也行，这个随意设计），然后就产生了如下的表：

<

element	0	1	2	3	4	5	6	7	8	9