正多面体有且只有5种，为什么？

正多面体有且只有5种，为什么？

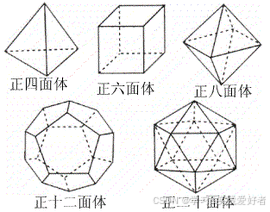
正多面体的特点：

    所有面都是全等的正多边形

    所有顶点处的二面角相等

    每个顶点处相交的面的数量相等

    整个多面体是封闭的（即它构成一个三维空间的有限封闭形状）。

解释一、从顶点处的角度和限制看

在三维空间中，若多个正多边形围绕一个顶点拼接，其内角之和必须满足：

内角和<360°.

原因：若内角和等于或超过 360°，这些面将无法在三维空间中“闭合”，只能平铺成平面（如蜂窝结构），无法形成凸多面体。设：

• 每个面是全等的正多边形（边数为 m，正m多边形）
• 每个顶点的结构完全相同（每个顶点连接 n 条边，亦即每个顶点处有n个面相交）。

由此切入思考

结论：五种正多面体

通过顶点处的角度和限制，仅存在五组可行的 (m,n)组合，对应五种正多面体：

正多面体                  面的形状 (m)     顶点连接边数 (n)     顶点内角和

正四面体                    正三角形 (3)        3                            180°

正八面体                    正三角形 (3)        4                            240°

正二十面体                正三角形 (3)        5                            300°

正六面体（立方体）  正方形 (4)           3                            270°

正十二面体                正五边形 (5)        3                            324°

解释二、从欧拉公式看

凸多面体有：

V – E + F = 2

其中 V、E、F 分别是顶点数（Vertex）、棱数（Edge）和面数（Face）。

分析边数E与顶点数V、面数F的关系，确定每个面有m条边（正m边形），每个顶点连接n条边（亦即每个顶点处有n个面相交）：

结论
仅存在五组解，对应五种正多面体：

1. 正四面体（m=3，n=3）。
2. 正八面体（m=3，n=4）。
3. 正二十面体（m=3，n=5）。
4. 正六面体，即立方体（m=4，n=3）。
5. 正十二面体（m=5，n=3）。

附录

附录1、凸正多面体及其欧拉公式验证：

1. 正四面体

• 顶点数 V=4，
• 棱数 E=6，
• 面数 F=4。

代入欧拉公式：

V−E+F=4−6+4=2

2. 立方体

• 顶点数 V=8，
• 棱数 E=12，
• 面数 F=6。

代入欧拉公式：

V−E+F=8−12+6=2.

3. 正八面体

• 顶点数 V=6，
• 棱数 E=12，
• 面数 F=8。

代入欧拉公式：

V−E+F=6−12+8=2.

4. 正十二面体

• 顶点数 V=20，
• 棱数 E=30，
• 面数 F=12。

代入欧拉公式：

V−E+F=20−30+12=2.

5. 正二十面体

• 顶点数 V=12，
• 棱数 E=30，
• 面数 F=20。

代入欧拉公式：

V−E+F=12−30+20=2

附录2、世界上只存在五种正多面体？https://zhuanlan.zhihu.com/p/265526766