GAP问题近似算法

  根据维基百科，背包问题（Knapsack problem）是一种组合优化的NP完全（NP-Complete，NPC）问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。NPC问题是没有多项式时间复杂度的解法的，但是利用近似算法，我们可以以伪多项式时间复杂度求解背包问题。一般来讲，背包问题有以下几种分类：
01背包问题
完全背包问题
多重背包问题

近似算法

定义

1. 近似比：A是问题I的近似算法，OPTA是问题I的最优算法，则定义近似算法A的近似比率为：
   
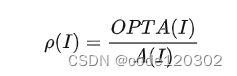
   最小化问题的近似比：
   
   近似比率总是>=1，近似比越小，算法越好。
2. 相对误差界：若对于输入规模为n的问题，存在一个函数$ϵ$(n)使得：
   
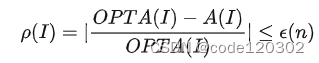
   近似算法的近似比率与相对误差界的关系：
   
3. 优化问题近似方案：把近似算法A的近似比满足如下条件：
   
   称为优化问题的近似方案。

Generalized Assignment Problem

指派问题（又称分配问题）在现实中有着广泛的应用背景，可以抽象为，m个物品与n个背包的匹配问题。GAP问题是组合优化中的一个分支，也是运筹学中的一类经典问题，且已被证明是NP-难问题。

一般求解方法，通常是从简单到复杂，先求解单背包分配问题，再逐步扩展到所有背包。

一种求解方法

Algorithm 1

M为背包的数量，N为物体的数量。p为N*M的矩阵，p[i,j]代表当物体i选择放入背包j时的收益。令算法A为单背包问题的解决方法。GAP问题的构建，从单背包问题开始，逐步使得所有背包都被分配一遍。
算法如下：

算法流程：
输入：j为当前背包的索引

1. 使用收益pj 运行单背包问题算法A，得到当前背包cj上被分配的物品集合$\overline{Sj}$。
2. 将收益函数p_j分为两部分，p1和p2(中间变量）。当i被分配到背包j中时或者当前遍历背包为j，那么p1代价值为p_j[i,j]，其余情况为0。用p_j减去p¹得到p2，p2作为下一轮遍历时的p，即p_j+1。
3. 当j < M时，继续调用Next-Bin函数。

算法示例：
给定四个items:{i1,i2,i3,i4}，三个bins:{c1,c2,c3}。调用上述算法，其处理过程如下图所示：

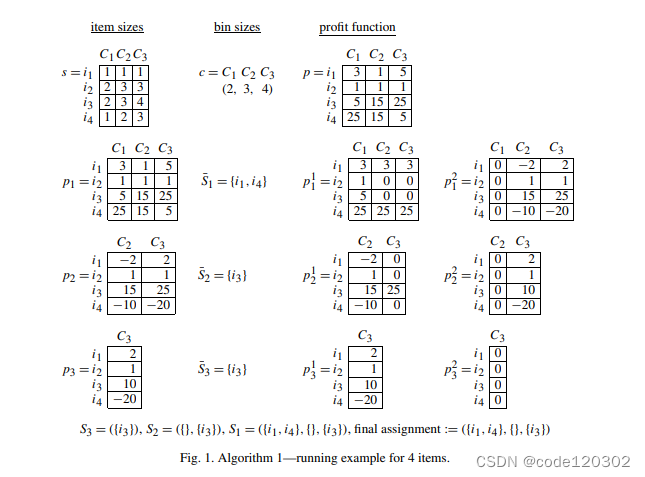
Algorithm 2

该部分为algorithm 1 的迭代版本。假设一个向量T，代表每个item的状态，若T[i] = -1，那么说明item i 没有被分配，若T[i] = j，表示item i被分配到cj上，且cj时它选择的最后一个bin。
算法如下：

Conclusion

该算法对于GAP的最大化问题能够保证2-approximation 的solution。

算法应用

边缘计算中的多用户多服务器场景

---

参考文献or资料：
【1】R. Cohen, L. Katzir, and D. Raz, “An efficient approximation for the generalized assignment problem,” Information Processing Letters, vol. 100, no. 4, pp. 162–166, 2006
【2】https://zhuanlan.zhihu.com/p/407171037
【3】https://bbs.huaweicloud.com/blogs/detail/195945